שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 311 - חידת חמשת הכלבים

    בשנת `1863`, סי. אף. דה יאניש דן לראשונה ב"חידת חמש המלכות" - להציב חמש מלכות על לוח השחמט כך שכל משבצת תותקף או תאוכלס - אשר הוצעה על ידי חברו, "מר דה ר.". יאניש הראה שאם אף מלכה לא יכולה לתקוף מלכה אחרת, ישנן תשעים ואחת דרכים שונות להציב את חמש המלכות, כאשר היפוכים ושיקופים אינם נחשבים כשונים. אם המלכות יכולות לתקוף זו את זו, תיעדתי מאות דרכים, אך לא ניתן למנות אותן במדויק.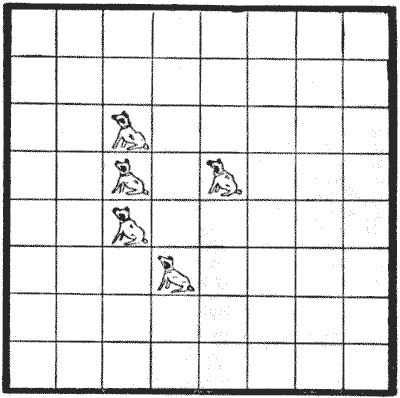 האיור אמור לייצג סידור של שישים וארבעה מְלוּנוֹת. ניתן לראות שחמש מְלוּנוֹת מכילות כל אחת כלב, ובבדיקה נוספת ניתן לראות שכל אחת משישים וארבע המְלוּנוֹת נמצאת בקו ישר עם לפחות כלב אחד - או אופקית, אנכית או באלכסון. קח כל מְלוּנָה שתרצה, ותגלה שתוכל למתוח קו ישר לכלב באחת משלוש הדרכים שהוזכרו. החידה היא להחליף את חמשת הכלבים ולגלות בכמה דרכים שונות ניתן להציב אותם בחמש מְלוּנוֹת בשורה ישרה, כך שכל מְלוּנָה תמיד תהיה בקו אחד עם לפחות כלב אחד. היפוכים ושיקופים נחשבים כאן כשונים.

  • שאלה 312 - סהרוני הירח של ביזנטיון

    כאשר פיליפוס ממקדוניה, אביו של אלכסנדר הגדול, מצא עצמו ניצב בפני קשיים גדולים במצור על ביזנטיון, הוא הורה לאנשיו לחתור תחת החומות. אולם, משאלותיו סוכלו, שכן לא חלף זמן רב לאחר תחילת הפעולות, עד שסהר ירח הופיע לפתע בשמים וחשף את תוכניותיו בפני יריביו. הביזנטים שמחו מטבע הדברים, וכדי להביע את הכרת התודה שלהם הקימו פסל לדיאנה, והסהר הפך מאז לסמל המדינה. במקדש שהכיל את הפסל הייתה רצפה מרובעת שהורכבה משישים וארבעה אריחים גדולים ויקרים. כולם היו פשוטים, למעט חמישה, שנשאו את סמל הסהר. חמשת אלה הוצבו מסיבות נסתרות כך שכל אריח יהיה תחת השגחה (כלומר, בקו ישר, אנכית, אופקית או אלכסונית) של לפחות אחד מהסהרונים. הסידור שאומץ על ידי האדריכל הביזנטי היה כדלקמן:—

     

    כעת, כיסוי אחד מחמשת הסהרונים הללו היה עבירה חמורה, שהעונש עליה היה מוות מכאיב וממושך מאוד. אבל לרגל חגיגה מסוימת היה צורך להניח על המרצפת הזו שטיח מרובע בגודל המרבי האפשרי, והראיתי באיור על ידי הצללה כהה את הממדים הגדולים ביותר שיהיו זמינים.

    החידה היא להראות כיצד האדריכל, אילו חזה את שאלת השטיח הזו, יכול היה לסדר את חמשת אריחי הסהר שלו בהתאם לתנאים הנדרשים, ובכל זאת לאפשר הנחת שטיח מרובע גדול ככל האפשר מבלי שאף אחד מחמשת אריחי הסהר יכוסה, או כל חלק מהם.

  • שאלה 313 - חידת מלכות ורץ

    יובחן שכל משבצת בלוח היא תפוסה או מותקפת. החידה היא להחליף רץ בצריח באותה המשבצת, ואז להניח את ארבע המלכות על משבצות אחרות כך שכל משבצת שוב תהיה תפוסה או מותקפת.

  • שאלה 314 - הצלב הדרומי

     

    באיור לעיל יש לנו חמישה כוכבי לכת ושמונים ואחד כוכבים קבועים, כאשר חמישה מהאחרונים מוסתרים על ידי כוכבי הלכת. ניתן לראות שכל כוכב, למעט עשרת הכוכבים שיש להם נקודה שחורה במרכזם, נמצא בקו ישר, אנכית, אופקית או באלכסון, עם לפחות אחד מכוכבי הלכת. החידה היא לסדר מחדש את כוכבי הלכת כך שכל הכוכבים יהיו בקו אחד עם אחד או יותר מהם.

    בסידור מחדש של כוכבי הלכת, כל אחד מחמשתם עשוי לנוע פעם אחת בקו ישר, בכל אחד משלושת הכיוונים שהוזכרו. הם, כמובן, יסתירו חמישה כוכבים אחרים במקום אלה המכוסים כעת.

  • שאלה 315 - חידת יתדות הכובעים

    הנה חידה בת חמש מלכות שהצגתי בצורה דמיונית בשנת `1897`. מכיוון שהמלכות יוצגו שם ככובעים על שישים וארבעה יתדות, אדבוק בכותרת, "חידת יתדות הכובעים". ניתן לראות שכל משבצת מאוכלסת או מותקפת. החידה היא להעביר מלכה אחת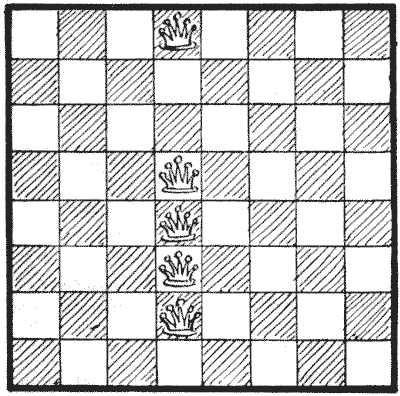 למשבצת אחרת כך שעדיין כל משבצת תהיה מאוכלסת או מותקפת, לאחר מכן להעביר מלכה שנייה בתנאים דומים, לאחר מכן מלכה שלישית, ולבסוף מלכה רביעית. לאחר המסע הרביעי כל משבצת חייבת להיות מותקפת או מאוכלסת, אך אף מלכה לא תתקוף מלכה אחרת. כמובן, שהמסעים לא חייבים להיות "מסעי מלכה"; ניתן להעביר מלכה לכל חלק בלוח.

  • שאלה 316 - האמזונות

    חידה זו מבוססת על חידה של קפטן טורטון. הסירו שלוש מלכות לריבועים אחרים כך שיישארו אחד-עשר ריבועים על הלוח שאינם מותקפים. הסרת שלוש המלכות אינה צריכה להתבצע על ידי "מהלכי מלכה". אתם יכולים פשוט להרים אותן ולהניח אותן בכל מקום. יש רק פתרון אחד.

  • שאלה 317 - חידה עם חיילים

    הנח שני חיילים באמצע לוח השחמט, אחד ב-Q `4` והשני ב-K `5`. כעת, הנח את ארבעה-עשר החיילים הנותרים (שישה-עשר בסך הכל) כך שאף שלושה לא יהיו בקו ישר בכל כיוון אפשרי.

    שים לב שאני בכוונה לא אומר מלכות, מכיוון שעל ידי המילים "בכל כיוון אפשרי" אני חורג מעבר להתקפות על אלכסונים. יש להתייחס לחיילים כנקודות בלבד במרחב - במרכזי הריבועים. ראה קווים מנוקדים במקרה של מס' `300`, "שמונה מלכות."

  • שאלה 318 - ציד אריות

     

    חברי, קפטן פות'ם הול, צייד חיות גדולות ידוע, אומר שאין דבר מלהיב יותר ממפגש עם עדר—להקה—צוות—מִשְׁפָּחָה—נחיל (לקח לי רבע שעה שלמה להיזכר במילה הנכונה, אבל סוף סוף מצאתי אותה)—גאווה של אריות. מדוע מספר אריות נקרא "גאווה," מספר לווייתנים נקרא "בית ספר," ומספר שועלים נקרא "רמייה" הן תעלומות של פילולוגיה שאליהן לא אכנס.

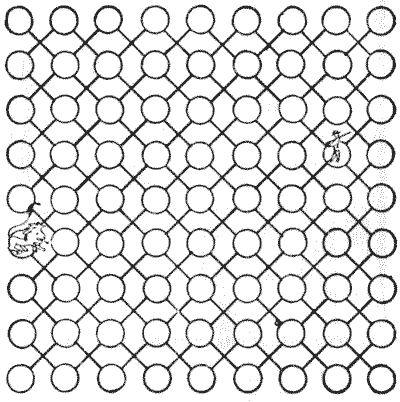
    ובכן, הקפטן אומר שאם אריה נמרץ חוצה את דרכך במדבר, זה נהיה תוסס, כי האריה בדרך כלל חיפש את האדם בדיוק כמו שהאדם חיפש את מלך היער. ובכל זאת כשהם נפגשים הם תמיד רבים ונלחמים. קצת התבוננות בסכסוך המצער והמתמשך הזה בין שתי משפחות מכובדות הובילה אותי להבין כמה חישובים לגבי הסבירות שהאדם והאריה יחצו זה את דרכו של זה בג'ונגל. בכל המקרים הללו צריך להתחיל בהנחות מסוימות פחות או יותר שרירותיות. לכן באיור לעיל חשבתי לנכון לייצג את השבילים במדבר בסדר מופתי כזה. למרות שהקפטן מבטיח לי שעקבות האריות בדרך כלל רצים בדרך הזו, יש לי ספקות.

    החידה היא פשוט לגלות בכמה דרכים שונות ניתן להציב את האדם והאריה בשני מקומות שונים שאינם על אותו נתיב. על ידי "נתיבים" יש להבין שאני מתייחס רק לקווים המצוירים. לפיכך, למעט ארבע הנקודות הפינתיות, כל לוחם נמצא תמיד בשני נתיבים ולא יותר. ניתן לראות שיש הרבה מקום להתחמק זה מזה במדבר, וזה בדיוק מה שתמיד הבינו.

  • שאלה 319 - שומרי האבירים

     

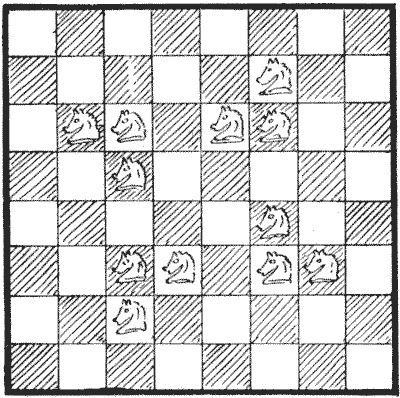
    האביר הוא הקומיקאי הנמוך חסר האחריות של לוח השחמט. "הוא נוכל מאוד לא בטוח, מתגנב ומדכא," אומר סופר אמריקאי. "הוא יכול לזוז רק שני ריבועים, אך מפצה על כמות התנועה שלו באיכותה, שכן הוא יכול לקפוץ ריבוע אחד הצידה ואחד קדימה בו זמנית, כמו חתול; יכול לעמוד על רגל אחת באמצע הלוח ולקפוץ לכל אחד משמונת הריבועים שהוא בוחר; יכול לעלות על צד אחד של גדר ולהשמיץ שלושה או ארבעה אנשים בצד השני; יש לו דרך מעוררת התנגדות להכניס את עצמו למקומות בטוחים שבהם הוא יכול להפחיד את המלך ולאלץ אותו לזוז, ואז לטרוף מלכה. לרוע טהור אין לאביר שווה, וכאשר אתה רודף אחריו מחור אחד הוא קופץ לאחר." נעשו ניסיונות שוב ושוב להשיג הגדרה קצרה, פשוטה ומדויקת של תנועת האביר—ללא הצלחה. זה באמת מורכב מלהזיז ריבוע אחד כמו צריח, ואז ריבוע אחר כמו רץ—שני הפעולות נעשות בקפיצה אחת, כך שלא משנה אם הריבוע הראשון שעוברים עליו תפוס על ידי כלי אחר או לא. זו, למעשה, התנועה הקופצת היחידה בשחמט. אבל קשה ככל שיהיה להגדיר, ילד יכול ללמוד את זה על ידי הסתכלות תוך מספר דקות.

    הראיתי בתרשים כיצד ניתן להציב שנים עשר אבירים (המספר הקטן ביותר האפשרי שיבצע את המשימה) על לוח השחמט כך שכל ריבוע יהיה או תפוס או מותקף על ידי אביר. בחן כל ריבוע בתורו, ותגלו שזה כך. כעת, החידה במקרה זה היא לגלות מהו המספר הקטן ביותר האפשרי של אבירים הנדרש כדי שכל ריבוע יהיה או תפוס או מותקף, וכל אביר מוגן על ידי אביר אחר. ואיך הייתם מסדרים אותם? יתברר שמתוך שנים עשר המוצגים בתרשים רק ארבעה מוגנים כך על ידי היותם במרחק מהלך של אביר מאביר אחר.

  • שאלה 320 - מסע הצריח

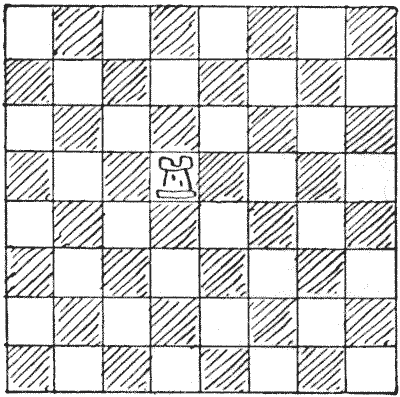    החידה היא להזיז את הצריח הבודד על פני כל הלוח, כך שהוא יבקר בכל משבצת בלוח פעם אחת בלבד, ויסיים את מסעו במשבצת ממנה הוא התחיל. עליכם לעשות זאת במספר המהלכים המינימלי האפשרי, ואם לא תהיו זהירים מאוד, תבצעו מהלך אחד יותר מדי. כמובן, משבצת נחשבת כ"מבוקרת" בין אם רק עוברים מעליה או הופכים אותה לתחנת עצירה, ולא נתווכח על הנקודה האם המשבצת המקורית מבוקרת פעמיים בפועל. נניח שהיא לא.