שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 271 - חידה של חמש עשרה אותיות

    ALE FOE HOD BGN
    CAB HEN JOG KFM
    HAG GEM MOB BFH
    FAN KIN JEK DFL
    JAM HIM GCL LJH
    AID JIB FCJ NJD
    OAK FIG HCK MLN
    BED OIL MCD BLK
    ICE CON DGK

    הטבלה מעל היא הפתרון לחידה שנתתי ב-Tit-bits בקיץ של `1896`. היה נדרש לקחת את האותיות A, B, C, D, E, F, G, H, I, J, K, L, M, N, ו-O, ויחד איתם ליצור שלושים וחמש קבוצות של שלוש אותיות כך שהצירופים יכללו את המספר הגדול ביותר האפשרי של מילים נפוצות באנגלית. אסור ששתי אותיות יופיעו יחד בקבוצה יותר מפעם אחת. לכן, A ו-L שהיו יחד ב-ALE, לעולם לא ימצאו יחד שוב; וגם אסור ש-A יופיע שוב בקבוצה עם E, או L עם E. תנאים אלה יתקיימו בפתרון לעיל, ומספר המילים שנוצרו הוא עשרים ואחת. אנשים רבים ניסו מאז קשה לנצח את המספר הזה, אבל עד כה לא הצליחו.

    לא ניתן ליצור יותר משלושים וחמישה צירופים של חמש עשרה האותיות במסגרת התנאים. מבחינה תיאורטית, לא יכולות להיווצר יותר מעשרים ושלוש מילים, מכיוון שרק מספר זה של צירופים אפשרי עם תנועה או תנועות בכל אחת מהן. ומכיוון שלא ניתן ליצור מילה באנגלית משלוש מהתנועות הנתונות (A, E, I ו-O), עלינו לצמצם את מספר המילים האפשריות לעשרים ושתיים. זה נכון מבחינה תיאורטית, אבל בפועל אי אפשר להשיג את המילה העשרים ושתיים הזו. אם JEK, המוצג לעיל, הייתה מילה, זה היה בסדר גמור; אבל זה לא, ושום כמות של להטוטנות עם שאר האותיות לא הביאה לתוצאה טובה יותר מהמוצגת. עלי לציין ששמות עצם וקיצורים, כמו Joe, Jim, Alf, Hal, Flo, Ike וכו', אינם מותרים.

    כעת, החידה הנוכחית היא וריאציה של הנ"ל. זה פשוט: במקום להשתמש בחמש עשרה האותיות הנתונות, הקורא רשאי לבחור כל חמש עשרה אותיות שונות של האלפבית שהוא מעדיף. לאחר מכן בנה שלושים וחמש קבוצות בהתאם לתנאים, והצג כמה שיותר מילים טובות באנגלית.

    נושאים:
    קומבינטוריקה

  • שאלה 272 - תשעת תלמידי בית הספר

    זוהי חידה נלווית חדשה ומעניינת ל"חמש עשרה תלמידות בית הספר" (ראו פתרון מס' `269`), ואפילו בצורה הפשוטה ביותר שבה אני מציג אותה יש קשיים שאין עליהם עוררין. תשעה תלמידי בית ספר יוצאים בשלשות בששת ימי השבוע כך שאף ילד לא הולך אי פעם זה לצד זה עם ילד אחר יותר מפעם אחת. איך הייתם מסדרים אותם?

    אם נציג אותם באמצעות תשע האותיות הראשונות של האלף-בית, הם עשויים להיות מקובצים ביום הראשון כדלקמן:—

    A B C
    D E F
    G H I

    אז A לעולם לא יכול ללכת שוב זה לצד זה עם B, או B עם C, או D עם E, וכן הלאה. אבל A יכול, כמובן, ללכת זה לצד זה עם C. זה כאן לא עניין של להיות ביחד באותה שלישייה, אלא של ללכת זה לצד זה בשלישייה. בתנאים אלה הם יכולים לצאת לטיול שישה ימים; בתנאי "תלמידות בית הספר" הם יכולים לטייל רק ארבעה ימים.

    נושאים:
    קומבינטוריקה

  • שאלה 273 - השולחן העגול

    להושיב את אותם n אנשים סביב שולחן עגול ב-

    `((n-1)(n-2))/2`

    מקרים כך שלאף אדם לא יהיו אותם שני שכנים פעמיים. זה, כמובן, שווה ערך לאמירה שכל אדם חייב לשבת פעם אחת, ורק פעם אחת, בין כל זוג אפשרי.

    נושאים:
    קומבינטוריקה

  • שאלה 274 - פאזל מלכודת העכברים

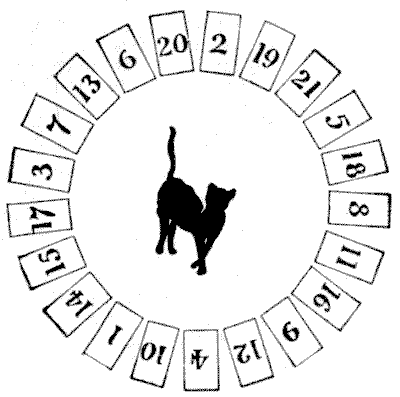    זוהי גרסה מודרנית, עם שינוי, של פאזל ישן בעל אותו השם. מספרו עשרים ואחד כרטיסים, `1, 2, 3` וכו', עד `21`, והניחו אותם במעגל בסדר המסוים המוצג באיור. כרטיסים אלה מייצגים עכברים. אתם מתחילים מכל כרטיס, קוראים לכרטיס הזה "אחד", וסופרים, "אחד, שתיים, שלוש" וכו', בכיוון השעון, וכאשר הספירה שלכם תואמת למספר על הכרטיס, ביצעתם "תפיסה", ואתם מסירים את הכרטיס. לאחר מכן התחילו בכרטיס הבא, קראו לו "אחד", ונסו שוב לבצע "תפיסה" נוספת. וכך הלאה. נניח שאתם מתחילים ב-`18`, וקוראים לכרטיס הזה "אחד", ה"תפיסה" הראשונה שלכם תהיה `19`. הסירו את `19` וה"תפיסה" הבאה שלכם היא `10`. הסירו את `10` וה"תפיסה" הבאה שלכם היא `1`. הסירו את `1`, ואם תספרו עד `21` (אסור לכם לחרוג), לא תוכלו לבצע "תפיסה" נוספת. כעת, האידיאל הוא "לתפוס" את כל עשרים ואחד העכברים, אך זה לא אפשרי כאן, ואם זה היה אפשרי, זה היה דורש רק עשרים ואחד ניסיונות שונים, לכל היותר, כדי להצליח. אבל הקורא רשאי להחליף בין שני כרטיסים לפני שהוא מתחיל. כך, אתם יכולים להחליף את ה-`6` עם ה-`2`, או את ה-`7` עם ה-`11`, או כל זוג אחר. ניתן לעשות זאת בכמה דרכים כדי לאפשר לכם "לתפוס" את כל עשרים ואחד העכברים, אם אז תתחילו במקום הנכון. לעולם אסור לכם לעבור על פני "תפיסה"; אתם תמיד חייבים להסיר את הכרטיס ולהתחיל מחדש.

  • שאלה 275 - שש עשרה כבשים

    הנה חידה חדשה עם גפרורים ומונים או מטבעות. באיור, הגפרורים מייצגים משוכות והמונים מייצגים כבשים. שש עשרה המשוכות מבחוץ, והכבשים, חייבים להיחשב כבלתי ניתנים להזזה; החידה קשורה כולה לתשע המשוכות מבפנים. ניתן לראות שכרגע תשע המשוכות האלה כולאות ארבע קבוצות של `8, 3, 3`, ו-`2` כבשים. החוואי צריך להתאים מחדש חלק מהמשוכות כך שיכלאו `6, 6`, ו-`4` כבשים. האם אתה יכול לעשות זאת על ידי החלפה של שתי משוכות בלבד? לאחר שהצלחת, נסה לעשות זאת על ידי החלפת שלוש משוכות; אחר כך ארבע, חמש, שש ושבע ברציפות. כמובן, המשוכות חייבות להיות מונחות כחוק על הקווים המקווקווים, ואסורים טריקים כמו השארת קצוות לא מחוברים של משוכות, או שתי משוכות המונחות זו לצד זו, או סתם גורמות למשוכות להחליף מקומות. למעשה, התנאים כל כך פשוטים שכל עובד חווה יבין זאת ישירות.

  • שאלה 276 - שמונה וילות

    באחד מפרבריה החיצוניים של לונדון היה לאיש חלקה מרובעת שעליה החליט לבנות שמונה וילות, כפי שמוצג באיור, עם שטח משחקים משותף באמצע. לאחר שהבתים הושלמו, וכולם או חלקם הושכרו, הוא גילה שמספר הדיירים בשלושת הבתים המרכיבים צד של הריבוע היה בכל מקרה תשעה. הוא לא ציין כיצד הדיירים התפלגו, אבל הראיתי במספרים בצדי הבתים דרך אחת שבה זה יכול היה לקרות. החידה היא לגלות את המספר הכולל של הדרכים שבהן כל הבתים או חלקם יכולים להיות מאוכלסים, כך שיהיו תשעה אנשים בכל צד. כדי שלא יהיו אי הבנות, אסביר שלמרות ש-B הוא מה שאנו מכנים שיקוף של A, אלה ייחשבו כשני הסדרים שונים, בעוד ש-C, אם הוא מסתובב, ייתן ארבעה הסדרים; ואם מסתובבים מול מראה, ארבעה הסדרים אחרים. יש לספור את כל שמונתם.

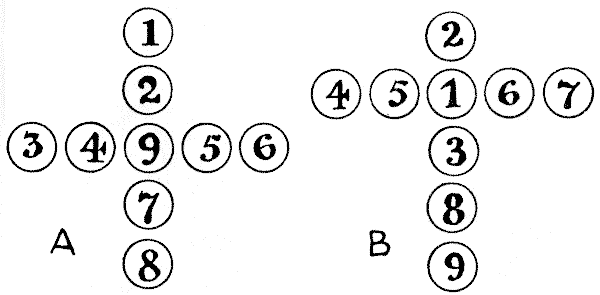
  • שאלה 277 - צלבים של מוֹנִים

    כל מה שאנחנו צריכים לפאזל הזה הם תשעה מוֹנִים, ממוספרים `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. ניתן לראות באיור A שהם מסודרים כך שיוצרים צלב יווני, ואילו במקרה של B הם יוצרים צלב לטיני. בשני המקרים הקורא יגלה שסכום המספרים באנך של הצלב זהה לסכום המספרים בזרוע האופקית. קל למדי להגיע לסידור כזה בניסוי וטעייה, אך הבעיה היא לגלות בדיוק בכמה דרכים שונות ניתן לעשות זאת בכל מקרה. זכרו שהיפוכים ושיקופים אינם נחשבים כשונים. כלומר, אם תסובבו את הדף הזה תקבלו ארבעה סידורים של הצלב היווני, ואם תסובבו אותו שוב מול מראה תקבלו ארבעה נוספים. אבל את שמונתם אלה מחשיבים כזהים. עכשיו, כמה דרכים שונות יש בכל מקרה?

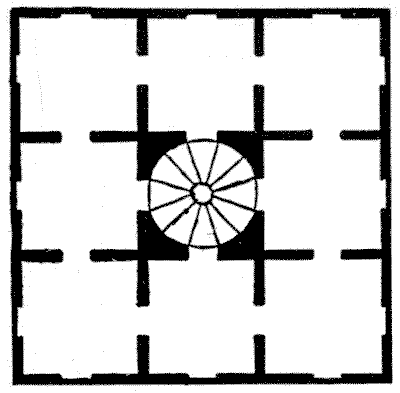
  • שאלה 278 - חידת מעונות

    במנזר מסוים היו שמונה מעונות גדולים בקומה אחת, שאליהם הגיעה גרם מדרגות ספירלי במרכז, כפי שמוצג בתרשים שלנו. בבדיקה שערכה אם המנזר ביום שני אחד, התגלה שהצד הדרומי מועדף כל כך, שפי שישה נזירות ישנו בצד הדרומי מאשר בכל אחד משלושת הצדדים האחרים. היא התנגדה לצפיפות היתר הזו, והורתה לצמצם אותה. ביום שלישי היא גילתה שפי חמש נזירות ישנו בצד הדרומי מאשר בכל אחד מהצדדים האחרים. שוב היא התלוננה. ביום רביעי היא מצאה פי ארבעה בצד הדרומי, ביום חמישי פי שלושה, וביום שישי פי שניים. לאחר שהאיצה בנזירות להמשיך במאמצים, היא שמחה לגלות ביום שבת שמספר שווה ישן בכל אחד מארבעת צדי הבית. מהו המספר הקטן ביותר של נזירות שיכול היה להיות שם, וכיצד הן יכלו להסתדר בכל אחד מששת הלילות? אסור שאף חדר יהיה ריק.

  • שאלה 279 - חביות הבלסם

     

    לסוחר מבגדד היו עשר חביות בלסם יקרות למכירה. הן היו ממוספרות, והיו מסודרות בשתי שורות, אחת על גבי השנייה, כפי שמוצג בתמונה. ככל שהמספר על החבית קטן יותר, כך ערכה גדול יותר. כך שהאיכות הטובה ביותר הייתה ממוספרת ב-"`1`" והגרועה ביותר ממוספרת ב-"`10`", וכל שאר המספרים מייצגים ערכים מדורגים. כעת, הכלל של אחמד אסן, הסוחר, היה שהוא לעולם לא הניח חבית מתחת או מימין לחבית בעלת ערך נמוך יותר. הסידור המוצג הוא, כמובן, הדרך הפשוטה ביותר לקיים תנאי זה. אבל ישנן דרכים רבות אחרות—כגון, לדוגמה, זו:—

    1 2 5 7 8
    3 4 6 9 10

    גם כאן, לאף חבית אין מספר קטן ממנה מימין או מתחתיה. החידה היא לגלות בכמה דרכים שונות יכול היה הסוחר מבגדד לסדר את חביותיו בשתי השורות מבלי להפר את הכלל שלו. האם תוכלו לספור את מספר הדרכים?

    נושאים:
    קומבינטוריקה

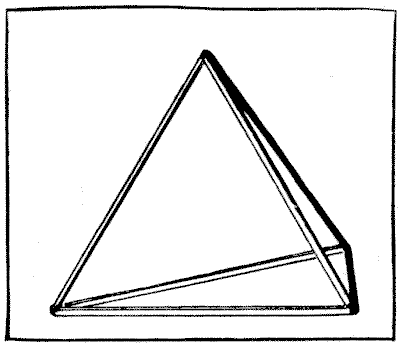
  • שאלה 280 - בניית הטטרהדרון

    יש לי טטרהדרון, או פירמידה משולשת, העשויה משישה מקלות המודבקים זה לזה, כפי שמוצג באיור. האם תוכלו לספור נכונה את מספר הדרכים השונות שבהן ניתן היה להדביק את ששת המקלות הללו יחד כדי ליצור את הפירמידה?

    כמה חברים עבדו על זה יחד בערב אחד, כאשר כל אדם מצטייד בשישה גפרורים כדי לעזור למחשבותיו; אבל התברר שאף שתי תוצאות לא היו זהות. אתם רואים, אם נסיר אחד מהמקלות ונסובב אותו לצד השני, זו תהיה פירמידה שונה. אם נחליף בין שניים מהמקלות התוצאה שוב תהיה שונה. אבל זכרו שניתן להעמיד כל פירמידה על כל אחד מארבעת צדדיה מבלי להיות פירמידה שונה. כמה דרכים יש בסך הכל?