שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 341 - ארבע הצפרדעים

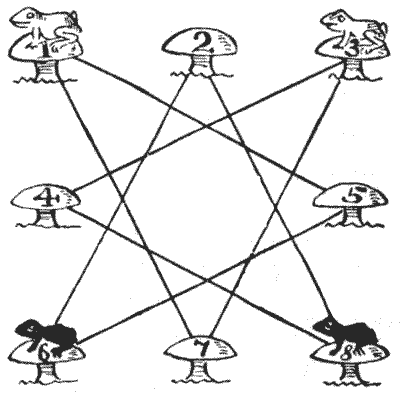    באיור יש לנו שמונה פטריות, עם צפרדעים לבנות על `1` ו-`3` וצפרדעים שחורות על `6` ו-`8`. החידה היא להזיז צפרדע אחת בכל פעם, בכל סדר, לאורך אחד הקווים הישרים מפטריה לפטריה, עד שהן החליפו מקומות, כשהצפרדעים הלבנות נשארות על `6` ו-`8` והשחורות על `1` ו-`3`. אם תשתמשו בארבעה אסימונים על דיאגרמה פשוטה, תגלו שזה די קל, אבל זה קצת יותר מבלבל לעשות זאת בשבעה מהלכים בלבד, כאשר כל מספר של מהלכים רצופים על ידי צפרדע אחת נחשב למהלך אחד. כמובן, יותר מצפרדע אחת לא יכולה להיות על פטריה בו זמנית.

  • שאלה 342 - החידה של המנדרין

    לחידה הבאה יש עניין נוסף מכיוון שפתרון נכון שלה הבטיח עבור סיני צעיר מסוים את ידה של כלתו המקסימה. המנדרין העשיר ביותר ברדיוס של מאה מייל מבייג'ינג היה היי-צ'אם-צ'ופ, ולבתו היפה, פיקי-בו, היו מעריצים רבים. אחד המאהבים הנלהבים ביותר שלה היה וינקי-היי, וכאשר הוא ביקש מהמנדרין הזקן את הסכמתו לנישואיהם, היי-צ'אם-צ'ופ הציג לו את החידה הבאה והבטיח את הסכמתו אם הצעיר יביא לו את התשובה הנכונה תוך שבוע. וינקי-היי, בעקבות הרגל הקיים בקרב פותרים מסוימים עד היום, נתן אותה לכל חבריו, וכאשר השווה את הפתרונות שלהם, הוא הגיש את הטוב ביותר כשלו. למרבה המזל זה היה ממש נכון. המנדרין מילא אז את הבטחתו. הגור השמן נהרג לכבוד חתונתם, וכאשר היי-צ'אם-צ'ופ העביר לווינקי-היי את כנף הכבד, כולם ידעו שזהו אות לנצחיות, בהתאם למנהג הסיני מאז ומעולם.

    למנדרין היה שולחן המחולק לעשרים וחמישה ריבועים, כפי שמוצג בתרשים. על כל אחד מעשרים וארבעה מהריבועים הללו הוצב מונה ממוספר, בדיוק כפי שציינתי. החידה היא להכניס את המונים לסדר מספרי על ידי הזזתם אחד בכל פעם במה שאנו מכנים "מהלכי אביר". מונה `1` צריך להיות במקום בו `16` נמצא, `2` במקום בו `11` נמצא, `4` במקום בו `13` נמצא כעת, וכן הלאה. ניתן לראות שכל המונים בריבועים המוצללים נמצאים במקומות הנכונים. כמובן, שני מונים לעולם לא יכולים להיות על ריבוע באותו זמן. האם אתה יכול לבצע את הפעלול במספר המהלכים הקטן ביותר האפשרי? 

     

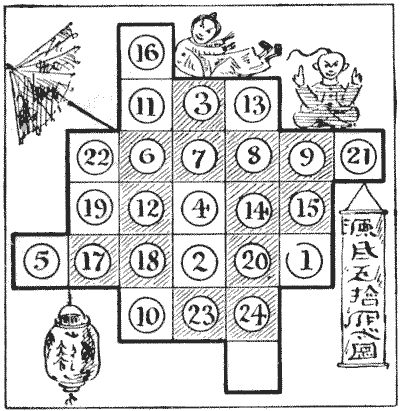
    על מנת להבהיר לחלוטין את אופן התנועה, אציין כי את מהלך האביר הראשון ניתן לבצע רק על ידי `1` או על ידי `2` או על ידי `10`. נניח ש-`1` זז, אז המהלך הבא חייב להיות על ידי `23, 4, 8`, או `21`. מכיוון שמעולם אין יותר מריבוע אחד פנוי, ניתן לרשום את סדר התנועה של המונים כדלקמן: `1`—`21`—`14`—`18`—`22`, וכו'. יש להכין תרשים גס בקנה מידה גדול יותר לצורך תרגול, ולהשתמש במונים ממוספרים או חתיכות קרטון.

  • שאלה 343 - תרגיל לאסירים

    להלן תוכנית האגף הצפוני של בית סוהר מסוים, המציגה את ששת-עשר התאים שכולם מתקשרים באמצעות פתחי דלתות פתוחים. חמישה-עשר אסירים מוספרו וסודרו בתאים כפי שמוצג. הורשה להם להחליף את תאיהם ככל שרצו, אך אם שני אסירים היו אי פעם באותו תא יחד, הובטח להם עונש חמור.

     

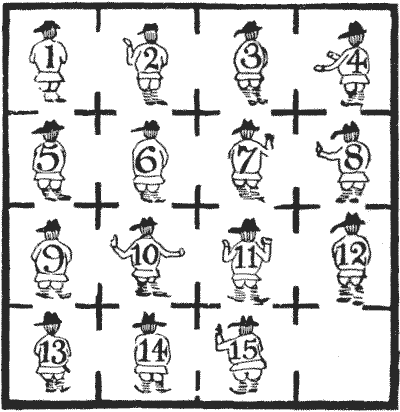
    כעת, על מנת להפחית את השמנת היתר הגוברת שלהם, ולשלב פעילות גופנית עם בילוי מנטלי, החליטו האסירים, בהצעתו של אחד ממספרם שהתעניין במסעי פרשים, לנסות ליצור לעצמם מסלול פרשים מושלם מבלי להפר את תקנות הכלא, ולהשאיר את תא הפינה הימנית התחתונה ריק, כפי שהיה במקור. הבדיחה בעניין היא שהסידור אליו הגיעו היה כדלקמן:—

    >
    8 3 12 1
    11 14 9 6
    4 7 2 13
    15 10 5

    הסוהרים לא הצליחו לזהות את העובדה החשובה שהגברים לא יכלו להגיע למצב הזה בלי ששניים מהם היו באיזשהו זמן באותו תא ביחד. נסו זאת עם אסימונים על דיאגרמה משורטטת, ותגלו שזה המצב. אחרת, הפתרון נכון מספיק, כאשר כל חבר נמצא, כנדרש, בתנועת פרש מהמספר הקודם, ותא הפינה המקורי ריק.

    החידה היא להתחיל כשהגברים ממוקמים כפי באיור ולהראות כיצד ניתן היה לעשות זאת במספר המהלכים המועט ביותר, תוך מתן מנוחה מלאה למספר האסירים הרב ביותר.

    מכיוון שמעולם אין יותר מתא ריק אחד עבור אדם להיכנס אליו, יש צורך רק לרשום את מספרי האנשים בסדר שבו הם נעים. ברור שמעט מאוד אנשים יכולים להישאר בתאים שלהם מבלי להפריע להם, אך אשאיר את הפותר לגלות כמה בדיוק, מכיוון שזה חלק מהותי מאוד מהחידה.

  • שאלה 344 - חידת המכלאה

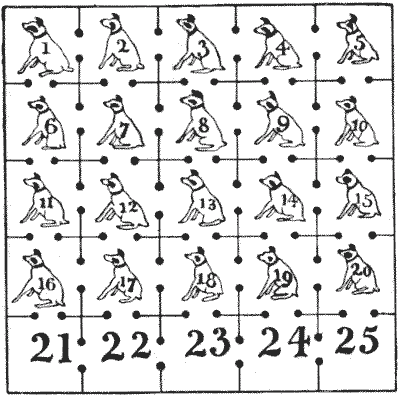    לאיש יש עשרים וחמש מכלאות כלבים, שכולן מתקשרות זו עם זו באמצעות פתחי דלתות, כפי שניתן לראות באיור. הוא מעוניין לסדר את עשרים הכלבים שלו כך שהם ייצרו מסלול פרש מכלב מספר `1` לכלב מספר `20`, כאשר השורה התחתונה של חמש המכלאות תישאר ריקה, כפי שהיא כעת. יש לעשות זאת על ידי העברת כלב אחד בכל פעם למכלאה פנויה. הכלבים מאומנים היטב לצייתנות, וניתן לסמוך עליהם שיישארו במכלאות שבהן הם ממוקמים, אלא אם כן שניים מהם ימוקמו באותה מכלאה יחד, הם יילחמו עד מוות. כיצד ניתן לפתור את החידה במספר המהלכים המועט ביותר האפשרי מבלי ששני כלבים יהיו יחד?

  • שאלה 345 - שני הרגלים

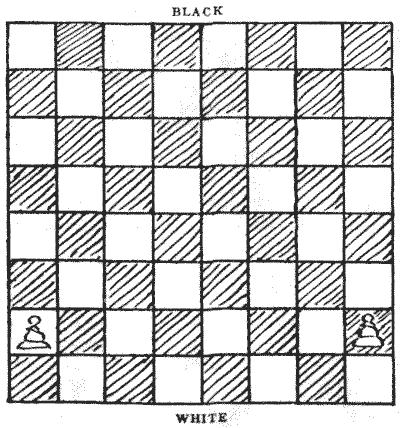    הנה חידה קטנה ומסודרת בספירה. בכמה דרכים שונות יכולים שני הרגלים להתקדם למשבצת השמינית? אתה רשאי להזיז אותם בכל סדר שתרצה כדי ליצור רצף שונה. לדוגמה, אתה יכול להזיז את הרגלי `Q R P` (משבצת אחת או שתיים) תחילה, או את הרגלי `K R P` תחילה, או רגלי אחד רחוק ככל שתרצה לפני שאתה נוגע בשני. כל רצף מותר, רק בחידה הזו ברגע שרגלי מגיע למשבצת השמינית הוא מת, ונשאר שם ללא המרה. האם אתה יכול לספור את מספר הרצפים השונים? בהתחלה זה ייראה לך קשה מאוד, אבל אני אראה שזה ממש פשוט כשמתקיפים את זה כמו שצריך.

  • שאלה 346 - הַצָּבַת הַלּוּחַ

    יש לי לוח שחמט בודד וסט כלי שחמט בודד. בכמה דרכים שונות ניתן להציב את הכלים בצורה נכונה לתחילת משחק? אני מגלה שרוב האנשים טועים בנקודה מסוימת בחישוב.

  • שאלה 347 - ספירת מלבנים

    האם תוכל לומר נכון כמה ריבועים ומלבנים אחרים מכילה לוח השחמט? במילים אחרות, בכמה דרכים שונות אפשר לציין ריבוע או מלבן אחר התחום על ידי קווים המפרידים בין ריבועי הלוח?

  • שאלה 348 - הצריח

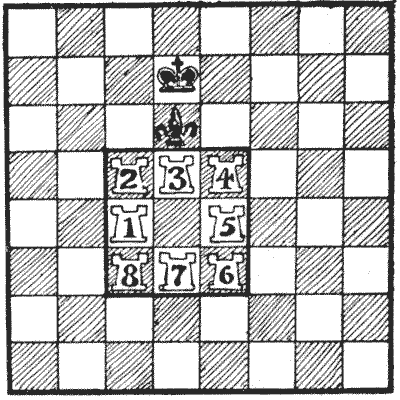    הצריחים הלבנים אינם יכולים לזוז מחוץ לריבוע הקטן שבו הם סגורים, למעט במהלך המסע האחרון, במתן מט. החידה היא כיצד לעשות מט לשחור במספר המהלכים המינימלי האפשרי עם צריח מס' `8`, כאשר שאר הצריחים נשארים בסדר מספרי סביב צדי הריבוע שלהם, עם ההפסקה בין `1` ל-`7`.

  • שאלה 349 - מבוי סתום

    לפני מספר שנים הוצעה החידה לבנות משחק שחמט דמיוני, שבו הלבן יהיה במצב של מבוי סתום (stale mate) במספר המהלכים המועט ביותר האפשרי, כאשר כל שלושים ושניים הכלים נמצאים על הלוח. האם תוכלו לבנות מצב כזה בפחות מעשרים מהלכים?

  • שאלה 350 - המלך הנשכח

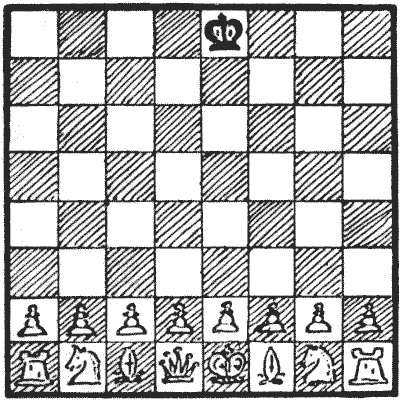    סדרו את הכלים במצב המוצג בתרשים. תנאי החידה הם: לבן משחק ומבצע מט בשישה מהלכים. למרות המורכבות, אראה כיצד ניתן לתמצת את מהלך המשחק למספר מצומצם של שורות, תוך ציון העובדה ששני המהלכים הראשונים של הלבן אינם ניתנים לשינוי.