חידות ורבוסים

זוהי קטגוריה כללית לחידות מחשבה הדורשות פיקחות, חשיבה יצירתית או זיהוי תבניות. רבוסים הם חידות מילים המשתמשות בתמונות, סמלים או אותיות לייצוג מילים או ביטויים. גרסאות הקשורות למתמטיקה עשויות לכלול רמזים מספריים או תפעוליים המוסתרים בפורמט חזותי.

חידות גפרורים שחזרו את התרגיל

  • הלוח בתאים

     

    איננו יכולים לחלק את לוח השחמט הרגיל לארבעה תאים ריבועיים שווים, ולתאר מסע שלם, או אפילו מסלול, בכל תא. אבל אנחנו יכולים לחלק אותו לארבעה תאים, כפי שמוצג באיור, שניים המכילים כל אחד עשרים משבצות, ושניים האחרים מכילים כל אחד שתים עשרה משבצות, ובכך להשיג חידה מעניינת. אתם מתבקשים לתאר מסע חוזר ונכנס שלם על הלוח הזה, החל מאיפה שתרצו, אך לבקר בכל משבצת בכל תא עוקב לפני שעוברים לתא אחר, ולבצע את הקפיצה הסופית חזרה למשבצת ממנה יצא הפרש. זה לא קשה, אבל יתגלה כמבדר מאוד ולא חסר תועלת.

    האם "מסע" חוזר ונכנס או "נתיב" פרש שלם אפשרי או לא על לוח מלבני ממדים נתונים תלוי לא רק בממדים שלו, אלא גם בצורה שלו. מסע אינו אפשרי באופן ברור על לוח המכיל מספר אי-זוגי של תאים, כגון `5` על `5` או `7` על `7`, מהסיבה הבאה: כל קפיצה עוקבת של הפרש חייבת להיות ממשבצת לבנה לשחורה ושחורה ללבנה לסירוגין. אבל אם יש מספר אי-זוגי של תאים או משבצות חייבת להיות משבצת אחת יותר מצבע אחד מאשר מהצבע השני, לכן הנתיב חייב להתחיל ממשבצת בצבע שנמצא בעודף, ולהסתיים בצבע דומה, ומכיוון שמהלך פרש מצבע אחד לצבע דומה הוא בלתי אפשרי, הנתיב לא יכול להיות חוזר ונכנס. אבל מסע מושלם יכול להתבצע על לוח מלבני בכל מימד, בתנאי שמספר המשבצות יהיה זוגי, ומספר המשבצות בצד אחד לא יהיה קטן מ-`6` ובצד השני לא יהיה קטן מ-`5`. במילים אחרות, הלוח המלבני הקטן ביותר שבו אפשרי מסע חוזר ונכנס הוא לוח בגודל `6` על `5`.

    נתיב פרש שלם (לא חוזר ונכנס) על פני כל המשבצות של לוח לעולם אינו אפשרי אם יש רק שתי משבצות בצד אחד; וגם לא אפשרי על לוח ריבועי ממדים קטנים מ-`5` על `5`. כך שעל לוח `4` על `4` אנחנו לא יכולים לתאר מסע פרש וגם לא נתיב פרש שלם; אנחנו חייבים להשאיר משבצת אחת לא מבוקרת. אבל על לוח `4` על `3` (המכיל ארבע משבצות פחות) ניתן לתאר נתיב שלם בשש עשרה דרכים שונות. זה עשוי לעניין את הקורא לגלות את כולן. כל נתיב שמתחיל ומסתיים במשבצות שונות נספר כאן כפתרון שונה, ואפילו מסלולים הפוכים נקראים שונים.

    מקורות:

  • מסע הפרשייה הקוביסטי

    לפני מספר שנים יצא לי לקרוא איפשהו שאבנית ונדרמונד, מתמטיקאי חכם שנולד ב-`1736` ונפטר ב-`1793`, הקדיש חלק ניכר מזמנו לחקר שאלת מסעי הפרש. מעבר למה שאפשר להבין מכמה אזכורים מקוטעים, אינני מודע לטבע המדויק או לתוצאות מחקריו, אך דבר אחד משך את תשומת ליבי, והייתה זו ההצהרה שהוא הציע את שאלת מסע הפרש על פני שש הפאות של קובייה, כאשר כל פאה היא לוח שחמט. בין אם השיג פתרון ובין אם לא, אינני יודע, אך מעולם לא ראיתי פתרון שפורסם. אז מיד התחלתי לעבוד כדי לשלוט בבעיה מעניינת זו. אולי הקורא ירצה לנסות זאת. מקורות:

  • ארבע הצפרדעים

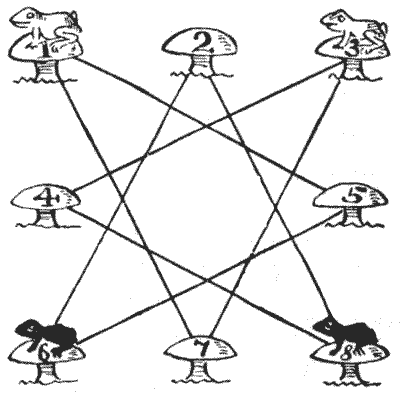    באיור יש לנו שמונה פטריות, עם צפרדעים לבנות על `1` ו-`3` וצפרדעים שחורות על `6` ו-`8`. החידה היא להזיז צפרדע אחת בכל פעם, בכל סדר, לאורך אחד הקווים הישרים מפטריה לפטריה, עד שהן החליפו מקומות, כשהצפרדעים הלבנות נשארות על `6` ו-`8` והשחורות על `1` ו-`3`. אם תשתמשו בארבעה אסימונים על דיאגרמה פשוטה, תגלו שזה די קל, אבל זה קצת יותר מבלבל לעשות זאת בשבעה מהלכים בלבד, כאשר כל מספר של מהלכים רצופים על ידי צפרדע אחת נחשב למהלך אחד. כמובן, יותר מצפרדע אחת לא יכולה להיות על פטריה בו זמנית. מקורות:

  • החידה של המנדרין

    לחידה הבאה יש עניין נוסף מכיוון שפתרון נכון שלה הבטיח עבור סיני צעיר מסוים את ידה של כלתו המקסימה. המנדרין העשיר ביותר ברדיוס של מאה מייל מבייג'ינג היה היי-צ'אם-צ'ופ, ולבתו היפה, פיקי-בו, היו מעריצים רבים. אחד המאהבים הנלהבים ביותר שלה היה וינקי-היי, וכאשר הוא ביקש מהמנדרין הזקן את הסכמתו לנישואיהם, היי-צ'אם-צ'ופ הציג לו את החידה הבאה והבטיח את הסכמתו אם הצעיר יביא לו את התשובה הנכונה תוך שבוע. וינקי-היי, בעקבות הרגל הקיים בקרב פותרים מסוימים עד היום, נתן אותה לכל חבריו, וכאשר השווה את הפתרונות שלהם, הוא הגיש את הטוב ביותר כשלו. למרבה המזל זה היה ממש נכון. המנדרין מילא אז את הבטחתו. הגור השמן נהרג לכבוד חתונתם, וכאשר היי-צ'אם-צ'ופ העביר לווינקי-היי את כנף הכבד, כולם ידעו שזהו אות לנצחיות, בהתאם למנהג הסיני מאז ומעולם.

    למנדרין היה שולחן המחולק לעשרים וחמישה ריבועים, כפי שמוצג בתרשים. על כל אחד מעשרים וארבעה מהריבועים הללו הוצב מונה ממוספר, בדיוק כפי שציינתי. החידה היא להכניס את המונים לסדר מספרי על ידי הזזתם אחד בכל פעם במה שאנו מכנים "מהלכי אביר". מונה `1` צריך להיות במקום בו `16` נמצא, `2` במקום בו `11` נמצא, `4` במקום בו `13` נמצא כעת, וכן הלאה. ניתן לראות שכל המונים בריבועים המוצללים נמצאים במקומות הנכונים. כמובן, שני מונים לעולם לא יכולים להיות על ריבוע באותו זמן. האם אתה יכול לבצע את הפעלול במספר המהלכים הקטן ביותר האפשרי? 

     

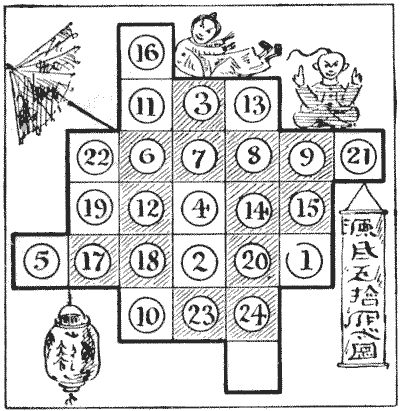
    על מנת להבהיר לחלוטין את אופן התנועה, אציין כי את מהלך האביר הראשון ניתן לבצע רק על ידי `1` או על ידי `2` או על ידי `10`. נניח ש-`1` זז, אז המהלך הבא חייב להיות על ידי `23, 4, 8`, או `21`. מכיוון שמעולם אין יותר מריבוע אחד פנוי, ניתן לרשום את סדר התנועה של המונים כדלקמן: `1`—`21`—`14`—`18`—`22`, וכו'. יש להכין תרשים גס בקנה מידה גדול יותר לצורך תרגול, ולהשתמש במונים ממוספרים או חתיכות קרטון.

    מקורות:

  • מבוי סתום

    לפני מספר שנים הוצעה החידה לבנות משחק שחמט דמיוני, שבו הלבן יהיה במצב של מבוי סתום (stale mate) במספר המהלכים המועט ביותר האפשרי, כאשר כל שלושים ושניים הכלים נמצאים על הלוח. האם תוכלו לבנות מצב כזה בפחות מעשרים מהלכים? מקורות:

  • מסע הצלב

    החידה הבאה היא חידת פרס שהוצגה על ידי לפני מספר שנים. הציגו משחק שחמט אשר, לאחר שישה עשר מסעים, ישאיר את הלבן עם כל ששת עשר הכלים שלו על המשבצות המקוריות שלהם ואת השחור מחזיק רק במלך שלו (לא בהכרח על המשבצת שלו). אז הלבן צריך לבצע מט כפוי בשלושה מסעים. מקורות:

  • דילמה מדהימה

    במשחק שחמט בין מר בלק ומר וייט, בלק היה במצב קשה, וכרגיל נאלץ לתפוס רכבת. לכן הציע שווייט ישלים את המשחק בהיעדרו בתנאי שלא יבוצעו מהלכים כלשהם עבור בלק, אלא רק עם הכלים הלבנים. מר וייט הסכים, אך לתדהמתו גילה שאי אפשר לנצח במשחק בתנאים כאלה. ככל שניסה, לא הצליח לעשות שחמט ליריבו. באיזו משבצת השאיר מר בלק את המלך שלו? שאר הכלים נמצאים בעמדותיהם הנכונות בתרשים. וייט רשאי להשאיר את בלק בשח כמה פעמים שירצה, כי זה לא משנה, מכיוון שהוא לעולם לא יוכל להגיע לעמדת שחמט. מקורות:

  • שַׁחְמָט מוּזָר

    האם תוכל להניח שני צריחים לבנים ופרש לבן על הלוח כך שהמלך השחור (שחייב להיות באחד מארבעת הריבועים באמצע הלוח) יהיה בשח, ללא אפשרות תנועה פתוחה עבורו? "במילים אחרות," יאמר הקורא, "המלך יוצג כמט." ובכן, אתה יכול להשתמש במונח אם תרצה, אם כי אני בכוונה לא משתמש בו בעצמי. העובדה הפשוטה שאין מלך לבן על הלוח תהיה סיבה מספקת לכך שאני לא עושה זאת. מקורות:

  • פאזל סיני עתיק

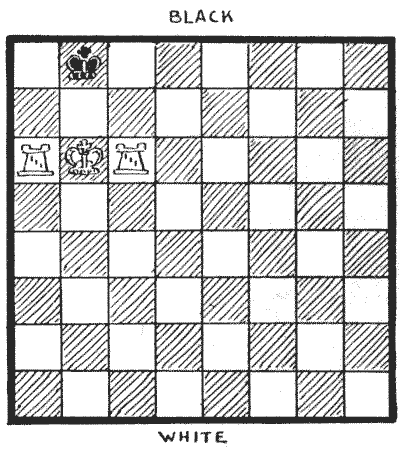    החידה הבאה שלי אמורה להיות סינית, בת מאות שנים, ותמיד מעניינת. לבן משחק ומבצע מט, על ידי הזזת כל אחד משלושת הכלים פעם אחת בלבד. מקורות:

  • סוליטר משבצות

    הנה משחק סוליטר קטן שהוא די קל, אבל לא כל כך קל שהוא לא מעניין. אתה יכול לסמן את הריבועים על גיליון קרטון או נייר, או שאתה יכול להשתמש בחלק מלוח השחמט שלך. הצגתי אסימונים ממוספרים באיור כדי להפוך את הפתרון לקל ומובן לכולם, אבל חיילי שחמט או דמקה יתאימו באותה מידה בפועל.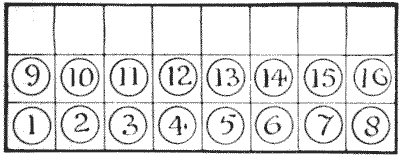 הפאזל הוא להסיר את כל האסימונים מלבד אחד, והאחד הזה שנשאר חייב להיות מס' `1`. אתה מסיר אסימון על ידי קפיצה מעל אסימון אחר למשבצת הבאה מעבר לו, אם המשבצת הזו פנויה, אבל אתה לא יכול לבצע קפיצה בכיוון אלכסוני. המהלכים הבאים יבהירו את המשחק: `1-9`, `2-10`, `1-2` וכן הלאה. כאן `1` קופץ מעל `9`, ואתה מסיר את `9` מהלוח; אז `2` קופץ מעל `10`, ואתה מסיר את `10`; אז `1` קופץ מעל `2`, ואתה מסיר את `2`. כל מהלך הוא אפוא לכידה, עד ללכידה האחרונה שנעשית על ידי מס' `1`. מקורות: