חידות ורבוסים

זוהי קטגוריה כללית לחידות מחשבה הדורשות פיקחות, חשיבה יצירתית או זיהוי תבניות. רבוסים הם חידות מילים המשתמשות בתמונות, סמלים או אותיות לייצוג מילים או ביטויים. גרסאות הקשורות למתמטיקה עשויות לכלול רמזים מספריים או תפעוליים המוסתרים בפורמט חזותי.

חידות גפרורים שחזרו את התרגיל

  • סיכת הָאֹדֶם

    בְּתוֹךְ דַּפֵּי יַעֲקוֹב סְקוֹטְלַנְד יַארְד נִמְצָאִים מִקְרֵי שׁוֹד תַּכְשִׁיטִים מְרַשְּׁמִים, אַךְ אֶחָד הַמְּסֻבָּכִים בְּיוֹתֵר הָיָה גְּנֵבַת הָאֲדָמִים שֶׁל לֵיְדִי לִיטֶלְוּוּד. הָיוּ, כַּמּוּבָן, גְּנֵבוֹת גְּדוֹלוֹת יוֹתֵר בְּמֻנָּחִים שֶׁל עֵרֶךְ, אַךְ מְעַטּוֹת הָיוּ מְפֻתָּלוֹת כָּל כָּךְ. לֵיְדִי לִיטֶלְוּוּד, מֵאֲחֻזַּת רוֹמְלִי, הָיְתָה יְרוּשָׁה יָפָה אַךְ קִיקְיוֹנִית מְעַט בְּצוּרַת סִיכַּת אֹדֶם. בְּעֵת שֶׁשָּׁהֲתָה בְּבֵיתָהּ שֶׁבָּעִיר בִּתְחִלַּת שְׁנוֹת הַשְּׁמוֹנִים הִיא לָקְחָה אֶת הַתַּכְשִׁיט לְחָנוּת בְּבְּרוֹמְפְּטוֹן לְתִקּוּנִים קַלִּים מְעַטִּים.

    "אֹסֶף מְעֻלֶּה שֶׁל אֲדָמִים, גְּבֶרֶת," אָמַר בַּעַל הַחֲנוּת, שֶׁלִּגְבִרְתָּהּ הָיָה זָר.

    "כֵּן," הֵשִׁיבָה; "אֲבָל דַּי לִפְלִיאָה כִּי לֹא סָפַרְתִּי אוֹתָם מַמָּשׁ אַף פַּעַם. אִמִּי הִצְבִּיעָה לְפָנַי פַּעַם שֶׁאִם מַתְחִילִים מֵהַמֶּרְכָּז וְסוֹפְרִים קַו אֶחָד לְמַעְלָה, לְאֹרֶךְ הַקָּצֶה וּלְמַטָּה בַּקַּו הַבָּא, תָּמִיד יֵשׁ שְׁמוֹנָה אֲדָמִים. כָּךְ תָּמִיד אֵדַע אִם חֲסֵרָה אֶבֶן.

     

    שִׁשָּׁה חֳדָשִׁים לְאַחַר מִכֵּן אָח שֶׁל לֵיְדִי לִיטֶלְוּוּד, שֶׁחָזַר מֵהָרֶגִימֶנְט שֶׁלּוֹ בְּהוֹדּוּ, שָׂם לֵב שֶׁאֲחוֹתוֹ עוֹנֶדֶת אֶת סִיכַּת הָאֹדֶם בְּאֶחָד הַלֵּילוֹת בְּנֶשֶׁף מְחוֹזִי, וּבַחֲזָרָתָם הַבַּיְתָה בִּקֵּשׁ לְהִסְתַּכֵּל בָּהּ מִקָּרוֹב יוֹתֵר. מִיָּד גִּלָּה אֶת הָעֻבְדָּה שֶׁאַרְבַּע מֵהָאֲבָנִים נֶעֶלְמוּ.

    "אֵיךְ זֶה אֶפְשָׁר?" אָמְרָה לֵיְדִי לִיטֶלְוּוּד. "אִם סוֹפְרִים קַו אֶחָד מֵהַמֶּרְכָּז, לְאֹרֶךְ הַקָּצֶה, וּלְמַטָּה בַּקַּו הַבָּא, בְּכָל כִּוּוּן, תָּמִיד יֵשׁ שְׁמוֹנֶה אֲבָנִים. זֶה תָּמִיד הָיָה כָּךְ וְכָךְ זֶה עַכְשָׁו. אֵיךְ אֵפוֹא אֶפְשָׁר לְהָסִיר אֶבֶן בְּלִי שֶׁאֲגַלֶּה אוֹתָהּ?"

    "שׁוּם דָּבָר לֹא יָכוֹל לִהְיוֹת פָּשׁוּט יוֹתֵר," הֵשִׁיב הָאָח. "אֲנִי מַכִּיר אֶת הַסִּיכָּה הֵיטֵב. בְּמָקוֹר הִיא הִכִּילָה אַרְבָּעִים וְחָמֵשׁ אֲבָנִים, וְעַכְשָׁו יֵשׁ רַק אַרְבָּעִים וְאַחַת. מִישֶׁהוּ גָּנַב אַרְבָּעָה אֲדָמִים, וְאָז הִתְקִין מֵחָדָשׁ מִסְפָּר קָטָן כְּכָל הָאֶפְשָׁר שֶׁל הָאֲחֵרוֹת בְּצוּרָה שֶׁתָּמִיד יִהְיוּ שְׁמוֹנֶה בְּכָל אֶחָד מֵהַכִּוּוּנִים שֶׁצִּיַּנְתְּ."

    לֹא הָיָה סָפֵק קַל שֶׁצּוֹרֵף בְּרוֹמְפְּטוֹן הָיָה הַגַּנָּב, וְהָעִנְיָן הֻנַּח בִּידֵי הַמִּשְׁטָרָה. אֲבָל הָאִישׁ הָיָה דָּרוּשׁ לְגְנֵבוֹת אֲחֵרוֹת, וְעָזַב אֶת הַשְּׁכוּנָה כְּבָר לִפְנֵי זְמַן מָה. עַד הַיּוֹם הַזֶּה הוּא מֵעוֹלָם לֹא נִמְצָא.

    הַנְּקֻדָּה הַקְּטַנָּה הַמְּעַנְיֶנֶת שֶׁתְּחִלָּה תִּסְכְּלָה אֶת הַמִּשְׁטָרָה, וְשֶׁמְּעַצֶּבֶת אֶת נוֹשֵׂא הַחִידָה שֶׁלָּנוּ, הִיא זוֹ: אֵיךְ סֻדְּרוּ בְּמָקוֹר אַרְבָּעִים וְחָמֵשׁ הָאֲדָמִים עַל הַסִּיכָּה? הַתַּרְשִׁים מַרְאֶה בְּדִיּוּק אֵיךְ סֻדְּרוּ אַרְבָּעִים וְאַחַת לְאַחַר שֶׁחָזְרָה מֵאֵת הַצּוֹרֵף; אֲבָל אַף עַל פִּי שֶׁהֵם סוֹפְרִים שְׁמוֹנֶה נָכוֹן בְּכָל אֶחָד מֵהַכִּוּוּנִים הַמֻּזְכָּרִים, חֲסֵרוֹת אַרְבַּע אֲבָנִים.

    מקורות:

  • מצא את אשת האיש

     

    יום אחד בקיץ בשנת `1903` הסתובבתי לאורך חזית ברייטון, צופה באנשים המטיילים על החוף, כאשר ידידי שליווה אותי משך לפתע את תשומת ליבי לאדם שעמד לבדו, ואמר, "האם תוכל להצביע על אשת האיש הזה? הם שוהים באותו מלון כמוני, והגברת היא אחת מאלה שנראות." לאחר מספר דקות של תצפית, הצלחתי לציין את הגברת בצורה נכונה. ידידי היה סקרן לדעת באיזו שיטת חשיבה הגעתי לתוצאה. זו הייתה תשובתי:—

    "אנו יכולים מיד להוציא מהכלל את אחות הרחמניות ואת הילדה בשמלה הקצרה; גם את האישה המוכרת תפוזים. זו לא יכולה להיות הגברת בבגדי אלמנות. זו לא הגברת בכיסא הגלגלים, כי היא לא שוהה במלון שלך, כי במקרה ראיתי אותה יוצאת מבית פרטי הבוקר בסיוע המשרתת שלה. שתי הנשים באדום סעדו ארוחת בוקר במלון שלי הבוקר, ומכיוון שלא לבשו בגדי חוץ, אני מסיק שהן שוהות שם. לכן זה נשען בין הגברת בכחול לזו עם השמשייה הירוקה. אבל היד השמאלית שמחזיקה את השמשייה היא, אתה רואה, לא מכוסה בכפפה ואין עליה טבעת נישואין. כתוצאה מכך, אני נאלץ למסקנה שהגברת בכחול היא אשת האיש הזה—ואתה אומר שזה נכון."

    כעת, מכיוון שידידי היה אמן, ומכיוון שחשבתי שאפשר להמציא חידה משעשעת על פי קווי השאלה שלו, ביקשתי ממנו להכין לי ציור לפי כמה הנחיות שנתתי לו, ויש לי תענוג להציג את התוצרת שלו לקוראים שלי. ניתן לראות שהתמונה מציגה שישה גברים ושש נשים: מס' `1, 3, 5, 7, 9` ו-`11` הן נשים, ומס' `2, 4, 6, 8, 10` ו-`12` הם גברים. שנים עשר האנשים האלה מייצגים שישה זוגות נשואים, שכולם זרים זה לזה, אשר, בהליכה חסרת מטרה, התערבבו. אבל אנחנו עוסקים רק באיש שחובש כובע קש—מספר `10`. החידה היא למצוא את אשת האיש הזה. בחנו את שש הנשים בקפידה, ובדקו אם תוכלו לקבוע מי מהן.

    הצגתי את התמונה באותה תקופה לכמה חברים, והם הביעו דעות שונות מאוד בנושא. אחד אמר, "אני לא מאמין שהוא יתחתן עם בחורה כמו מספר `7`." אחר אמר, "אני בטוח שבחורה נחמדה כמו מספר `3` לא תתחתן עם בחור כזה!" אחר אמר, "זה חייב להיות מספר `1`, כי היא התרחקה ככל האפשר מהבהמה!" הוצע שוב, שזה חייב להיות מספר `11`, כי "נראה שהוא מסתכל לעברה;" אבל ציניקן השיב, "בגלל אותה סיבה, אם הוא באמת מסתכל עליה, אני צריך לומר שהיא לא אשתו!"

    אני משאיר כעת את השאלה בידי הקוראים שלי. מי באמת אשתו של מספר `10`?

    האיור מצומצם בהכרח מאוד מהקנה מידה הגדול שבו הוא הופיע במקור בThe Weekly Dispatch (24 במאי `1903`), אך יש לקוות שהפרטים יהיו ברורים דיים כדי לאפשר לקורא להפיק בידור מבחינתו. בכל מקרה, הפתרון הניתן יאפשר לו לעקוב אחר הנקודות בעניין.


     

    מקורות:

  • שאלה

    הזיזו גפרור אחד, כך שיתקבל שוויון תקין.

    הערה: יתכנו מספר פתרונות.

    מקורות:

  • שורש הגפרור

    הזז גפרור אחד וקבל שוויון נכון:

  • 5 ריבועים

    הזיזו שלושה גפרורים כדי לקבל 5 ריבועים:

  • 7=8-5?

    יש להסיר שני גפרורים כדי להפוך את השוויון הבא לנכון:

    מקורות:

  • כיסא הפוך

    הכיסא התהפך, צריך להזיז שני גפרורים כדי להחזיר אותו למקומו המקורי.

  • תן 2 קבל 4

    הוסיפו 2 גפרורים כך שיתקבלו בדיוק 4 ריבועים:

  • חידת גפרורים חדשה

    באיור מוצגים שמונה-עשר גפרורים המסודרים כך שהם תוחמים שני שטחים, כאשר אחד גדול פי שניים מהשני. האם תוכלו לסדר אותם מחדש (`1`) כך שיתחמו שני שטחים מרובעים, כאשר אחד גדול בדיוק פי שלושה מהשני, ו- (`2`) כך שיתחמו שני שטחים מחומשים, כאשר אחד גדול בדיוק פי שלושה מהשני? יש להשתמש בכל שמונה-עשר הגפרורים בצורה הוגנת בכל מקרה; שני השטחים חייבים להיות מופרדים לחלוטין, ולא צריכים להיות קצוות רופפים או גפרורים כפולים. מקורות:

  • מִכְלְאוֹת שֵׁשׁ הַכְּבָשִׂים

     

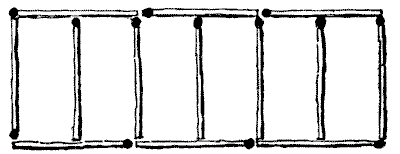
    הִנֵּה חִידָה קְטַנָּה חֲדָשָׁה עִם גּוּפְרִיתִים. כְּפִי שֶׁנִּיתָן לִרְאוֹת בְּאִיּוּר, שְׁלוֹשָׁה עָשָׂר גּוּפְרִיתִים, הַמְּיַצְּגִים מַעֲבָרִים שֶׁל חוֹלֵף, מֻנָּחִים כָּךְ שֶׁהֵם תּוֹחֲמִים שֵׁשׁ מִכְלְאוֹת כְּבָשִׂים בְּאוֹתוֹ גֹּדֶל. עַכְשָׁו, אֶחָד מִמַּעֲבָרִים אֵלֶּה נִגְנַב, וְהַחוֹלֵף עֲדַיִן רָצָה לִתְחוֹם שֵׁשׁ מִכְלָאוֹת בְּגֹּדֶל שָׁוֶה עִם שְׁנֵים עָשָׂר הַגּוּפְרִיתִים שֶׁנִּשְׁאֲרוּ. אֵיךְ הוּא הָיָה צָרִיךְ לַעֲשׂוֹת אֶת זֶה? יֵשׁ לְהִשְׁתַּמֵּשׁ בְּהֶגְיוֹן בְּכָל שְׁנֵים הֶעָשָׂר הַגּוּפְרִיתִים, וְלֹא צְרִיכִים לִהְיוֹת גּוּפְרִיתִים כְּפוּלִים אוֹ קְצוֹת רוֹפְפִים.

    מקורות: