חידות ורבוסים
זוהי קטגוריה כללית לחידות מחשבה הדורשות פיקחות, חשיבה יצירתית או זיהוי תבניות. רבוסים הם חידות מילים המשתמשות בתמונות, סמלים או אותיות לייצוג מילים או ביטויים. גרסאות הקשורות למתמטיקה עשויות לכלול רמזים מספריים או תפעוליים המוסתרים בפורמט חזותי.
חידות גפרורים שחזרו את התרגיל-
פאזל קוביות האותיות

הנה תזכורת קטנה לחברנו הוותיק, פאזל חמש-עשרה הבלוקים. שמונה קוביות עץ מסומנות באותיות, וממוקמות בקופסה, כפי שמוצג באיור. ניתן לראות שאפשר להזיז רק קובייה אחת בכל פעם למקום הפנוי באותו רגע, מכיוון שאף קובייה לא יכולה להיות מורמת מהקופסה. הפאזל הוא להזיז אותן עד שמקבלים אותן בסדר הזה—
A B C
D E F
G Hתגלו שזה לא קשה בכלל אם מותר לכם לבצע כמה מהלכים שתרצו. אבל הפאזל הוא לעשות את זה במספר המהלכים המועט ביותר האפשרי. אני לא אציין מה המספר הקטן ביותר הזה, כי ייתכן שהקורא ירצה לגלות זאת בעצמו. כשאתם רושמים את המהלכים שלכם, תגלו שאתם צריכים לרשום רק את האותיות בסדר שבו הן מוזזות. לדוגמה, חמשת המהלכים הראשונים שלכם עשויים להיות C, H, G, E, F; ולציון הזה לא יכולה להיות שום דו-משמעות. בפועל, אתם צריכים רק שמונה אסימונים ודיאגרמה פשוטה על דף נייר.
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 219
-
קושי בבית דירות
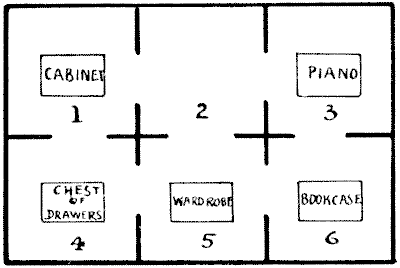 משפחת דובסון שכרה דירות בסלוקום-און-סי. היו שישה חדרים באותה קומה, כולם מחוברים, כפי שמוצג בתרשים. החדרים שהם לקחו היו מספרים `4, 5`, ו-`6`, כולם פונים לים. אבל התעוררה בעיה קטנה. מר דובסון התעקש שהפסנתר וארון הספרים יחליפו חדרים. זה היה ערמומי, כי משפחת דובסון לא הייתה מוזיקלית, אבל הם רצו למנוע מכל אחד אחר לנגן בכלי הנגינה. עכשיו, החדרים היו קטנים מאוד ופריטי הריהוט שצוינו היו גדולים מאוד, כך שלא ניתן היה להכניס שניים מהפריטים הללו לאף חדר באותו זמן. איך ניתן לבצע את ההחלפה עם מינימום עבודה? נניח, לדוגמה, שאתה מעביר תחילה את הארון לבגדים למספר `2`; אז אתה יכול להעביר את ארון הספרים למספר `5` ואת הפסנתר למספר `6`, וכן הלאה. זו חידה מרתקת, אבל לבעלת הבית היו סיבות לא להעריך אותה. נסה לפתור את הקושי שלה במספר המינימלי האפשרי של העברות עם אסימונים על דף נייר.
מקורות:
משפחת דובסון שכרה דירות בסלוקום-און-סי. היו שישה חדרים באותה קומה, כולם מחוברים, כפי שמוצג בתרשים. החדרים שהם לקחו היו מספרים `4, 5`, ו-`6`, כולם פונים לים. אבל התעוררה בעיה קטנה. מר דובסון התעקש שהפסנתר וארון הספרים יחליפו חדרים. זה היה ערמומי, כי משפחת דובסון לא הייתה מוזיקלית, אבל הם רצו למנוע מכל אחד אחר לנגן בכלי הנגינה. עכשיו, החדרים היו קטנים מאוד ופריטי הריהוט שצוינו היו גדולים מאוד, כך שלא ניתן היה להכניס שניים מהפריטים הללו לאף חדר באותו זמן. איך ניתן לבצע את ההחלפה עם מינימום עבודה? נניח, לדוגמה, שאתה מעביר תחילה את הארון לבגדים למספר `2`; אז אתה יכול להעביר את ארון הספרים למספר `5` ואת הפסנתר למספר `6`, וכן הלאה. זו חידה מרתקת, אבל לבעלת הבית היו סיבות לא להעריך אותה. נסה לפתור את הקושי שלה במספר המינימלי האפשרי של העברות עם אסימונים על דף נייר.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 220
-
שמונה מנועים
הדיאגרמה מייצגת את חצר המנועים של חברת רכבות תחת ניהול אקסצנטרי. מותר למנועים להיות נייחים רק בתשע הנקודות המצוינות, שאחת מהן פנויה כרגע. נדרש להזיז את המנועים, אחד בכל פעם, מנקודה לנקודה, בשבע עשרה מהלכים, כך שמספריהם יהיו בסדר מספרי סביב המעגל, כאשר הנקודה המרכזית נשארת פנויה. אבל אחד המנועים הוציא את האש שלו, ולכן הוא לא יכול לזוז. איך עושים את זה? ואיזה מנוע נשאר נייח לאורך כל הדרך?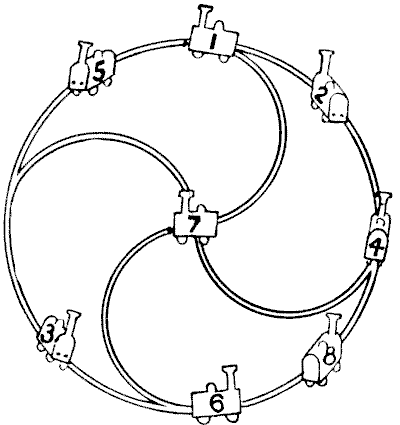 מקורות:נושאים:חידות ורבוסים
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 221
-
תַּסְבִּיךְ מְסִלַּת בַּרְזֶל
התכנית מייצגת חלק מקו הרכבת של חברת הרכבות לונדון, קלודוויל ומדפורד. זהו קו בודד עם לולאה. יש מקום רק לשמונה קרונות, או שבעה קרונות וקטר, בין B ל-C או בקו השמאלי או בקו הימני של הלולאה. קרה ששתי רכבות משא (שכל אחת מהן מורכבת מקטר ושישה עשר קרונות) נכנסו למצב המוצג באיור. זה נראה כמו מבוי סתום חסר תקווה, וכל נהג קטר רצה שהשני יחזור לתחנה הבאה ויוריד תשעה קרונות. אבל מסיק גאון לקח על עצמו להעביר את הרכבות ולשלוח אותן למסעותיהן בהתאמה, כאשר הקטרים שלהם נמצאים כראוי מלפנים. הוא גם הצליח להפוך את כיוון הקטרים במספר הפעמים המועט ביותר האפשרי. האם היית יכול לבצע את המשימה? וכמה פעמים היית צריך להפוך את כיוון הקטרים? "היפוך כיוון" פירושו שינוי כיוון, אחורה או קדימה. אסור לבצע עבודות הרמה בחבל, הרמה בתעופה או טריקים אחרים. כל העבודה חייבת להתבצע באופן לגיטימי על ידי שני הקטרים. זוהי חידה פשוטה אך מעניינת אם מנסים אותה עם אסימונים.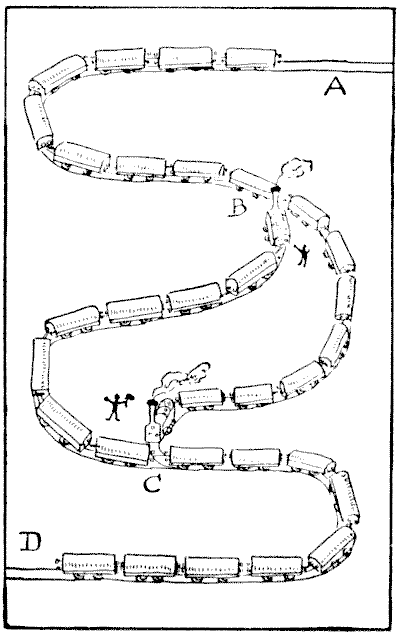 מקורות:נושאים:חידות ורבוסים
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 223
-
חידת מוסך המכוניות
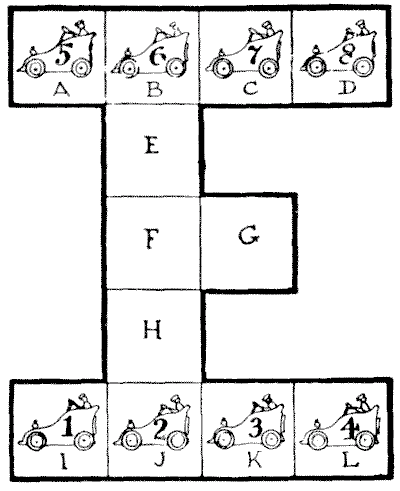
הקשיים של בעל מוסך מוסבים למעין בילוי שיש בו קסם מיוחד. כל מה שצריך זה להכין תוכנית או דיאגרמה פשוטה על דף נייר או קרטון ולמספר שמונה אסימונים, מ-`1` עד `8`. אז משפחה שלמה יכולה להיכנס לתחרות משעשעת כדי למצוא את הפתרון הטוב ביותר לקושי.
האיור מייצג את תוכנית מוסך המכוניות, עם מקום לשתים עשרה מכוניות. אבל השטח מצומצם בצורה לא נוחה, ולכן הבעלים נתקל לעתים קרובות במבוכה רבה. נניח, למשל, ששמונה המכוניות הממוספרות מ-`1` עד `8` נמצאות במקומות המוצגים, איך ניתן להזיז אותן בצורה המהירה ביותר כך ש-`1, 2, 3` ו-`4` יחליפו מקומות עם `5, 6, 7` ו-`8` — כלומר, כשהמספרים עדיין רצים משמאל לימין, כפי שהם כרגע, אבל השורה העליונה הוחלפה בשורה התחתונה? מהו המספר הקטן ביותר של מהלכים אפשריים?
מכונית אחת זזה בכל פעם, וכל מרחק נחשב למהלך אחד. כדי למנוע אי הבנות, מקומות העצירה מסומנים בריבועים, ויכולה להיות רק מכונית אחת בריבוע בכל פעם.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 224
-
עשרת האסירים
אילו לבתי הכלא לא היה שימוש אחר, עדיין ניתן היה לשמר אותם לתועלתם המיוחדת של יוצרי החידות. נראה שהם מכרה בלתי נדלה של רעיונות מבלבלים. הנה שאלה קטנה שאולי תעניין את הקורא לתקופה קצרה. באיור יש לנו כלא של שישה עשר תאים. ניתן לראות את מיקומם של עשרת האסירים. לסוהר יש אמונות תפלות מוזרות לגבי מספרים אי-זוגיים וזוגיים, והוא רוצה לסדר מחדש את עשרת האסירים כך שיהיו כמה שיותר שורות זוגיות של אנשים, אנכית, אופקית ואלכסונית. נכון לעכשיו ניתן לראות, כפי שמצוין על ידי החצים, שיש רק שתים עשרה שורות כאלה של `2` ו-`4`. אני אצהיר מיד שהמספר הגדול ביותר של שורות כאלה שאפשר הוא שש עשרה. אבל הסוהר מרשה להעביר רק ארבעה אנשים לתאים אחרים, ומודיע לי, שכיוון שהאיש שיושב בפינה הימנית התחתונה חולה, אסור להזיז אותו. עכשיו, איך נשיג את שש עשרה השורות האלה של מספרים זוגיים בתנאים כאלה?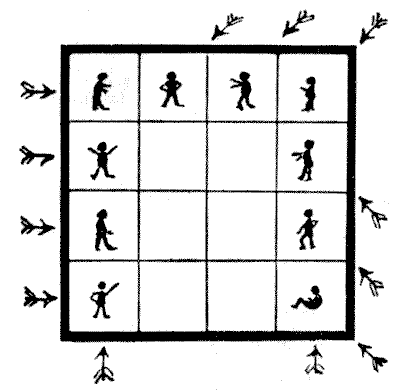 מקורות:נושאים:חידות ורבוסים
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 225
-
סובב את החוף
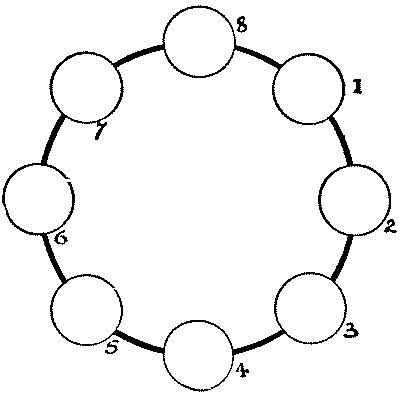 הנה חידה שלדעתי תהיה משעשעת כמו שהיא מלמדת. נתון לנו מעגל של שמונה עיגולים. כאשר עיגול `8` ריק, עלינו לכתוב את שמה של עיר נמל בת שבע אותיות בממלכה המאוחדת באופן הזה. געו בעיגול ריק עם העיפרון שלכם, ואז קפצו מעל שני עיגולים בכל כיוון מסביב למעגל, וכתבו את האות הראשונה. לאחר מכן געו בעיגול ריק אחר, קפצו מעל שני עיגולים, וכתבו את האות השנייה. המשיכו באופן דומה עם שאר האותיות בסדר הנכון שלהן עד שתשלימו את המילה. לדוגמה, נניח שנבחר ב-"Glasgow," ונמשיך כדלקמן: `6`—`1, 7`—`2, 8`—`3, 7`—`4, 8`—`5`, מה שאומר שאנחנו נוגעים ב-`6`, קופצים מעל `7`, וכותבים "G" על `1`; לאחר מכן נוגעים ב-`7`, קופצים מעל `8` ו-`1`, וכותבים "l" על `2`; וכן הלאה. יתברר שאחרי שכתבנו את חמש האותיות הראשונות - "Glasg" - כמו לעיל, אנחנו לא יכולים להמשיך הלאה. או שיש משהו לא בסדר עם "Glasgow," או שלא הצלחנו לבצע את הקפיצות שלנו כראוי. האם תוכלו לרדת לשורש התעלומה?
מקורות:
הנה חידה שלדעתי תהיה משעשעת כמו שהיא מלמדת. נתון לנו מעגל של שמונה עיגולים. כאשר עיגול `8` ריק, עלינו לכתוב את שמה של עיר נמל בת שבע אותיות בממלכה המאוחדת באופן הזה. געו בעיגול ריק עם העיפרון שלכם, ואז קפצו מעל שני עיגולים בכל כיוון מסביב למעגל, וכתבו את האות הראשונה. לאחר מכן געו בעיגול ריק אחר, קפצו מעל שני עיגולים, וכתבו את האות השנייה. המשיכו באופן דומה עם שאר האותיות בסדר הנכון שלהן עד שתשלימו את המילה. לדוגמה, נניח שנבחר ב-"Glasgow," ונמשיך כדלקמן: `6`—`1, 7`—`2, 8`—`3, 7`—`4, 8`—`5`, מה שאומר שאנחנו נוגעים ב-`6`, קופצים מעל `7`, וכותבים "G" על `1`; לאחר מכן נוגעים ב-`7`, קופצים מעל `8` ו-`1`, וכותבים "l" על `2`; וכן הלאה. יתברר שאחרי שכתבנו את חמש האותיות הראשונות - "Glasg" - כמו לעיל, אנחנו לא יכולים להמשיך הלאה. או שיש משהו לא בסדר עם "Glasgow," או שלא הצלחנו לבצע את הקפיצות שלנו כראוי. האם תוכלו לרדת לשורש התעלומה?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 226
-
סוליטר מרכזי
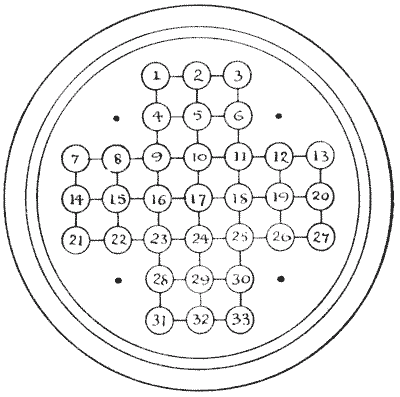
החידה העתיקה הזו הייתה חביבה מאוד על סבתותינו, ורובנו, אני מתאר לעצמי, נתקלנו מדי פעם בלוח "סוליטר" — לוח עגול מלוטש עם חורים החתוכים בו בדוגמה גיאומטרית, וגולה זכוכית בכל חור. לפעמים שמתי לב לאחד על שולחן צדדי בטרקלין קדמי פרברי, או שמצאתי אחד על מדף בקוטג' כפרי, או ששמו לב לאחד בפונדק דרכים. לפעמים הם מהצורה המוצגת לעיל, אך נפוץ באותה מידה שהלוח יהיו לו ארבעה חורים נוספים, בנקודות המסומנות בנקודות. אני בוחר בצורה הפשוטה יותר.
אף על פי שלוחי "סוליטר" עדיין נמכרים בחנויות הצעצועים, די יהיה אם הקורא יכין עותק מוגדל של הנ"ל על גיליון קרטון או נייר, ימספר את ה"חורים," ויספק לעצמו `33` אסימונים, כפתורים או שעועית. כעת הניחו אסימון בכל חור פרט למרכזי, מס' `17`, והחידה היא להסיר את כל האסימונים בסדרת קפיצות, למעט האסימון האחרון, שאותו יש להשאיר בחור המרכזי הזה. מותר לך לקפוץ אסימון אחד מעל האסימון הבא לחור פנוי מעבר לו, בדיוק כמו במשחק הדמקה, והאסימון שקפצו מעליו מוסר מיד מהלוח. רק זכור שכל מהלך חייב להיות קפיצה; כתוצאה מכך תסיר אסימון בכל מהלך, ושלושים ואחת קפיצות בודדות כמובן יסירו את כל שלושים ואחד האסימונים. אבל מותרים מהלכים מורכבים (כמו בדמקה, שוב), כל עוד אסימון אחד ממשיך לקפוץ, כל הקפיצות נחשבות למהלך אחד.
הנה ההתחלה של פתרון דמיוני שישמש כדי להבהיר לחלוטין את אופן התנועה, ולהראות כיצד הפותר צריך לכתוב את ניסיונותיו: `5-17`, `12-10`, `26-12`, `24-26` (`13-11`, `11-25`), `9-11` (`26-24`, `24-10`, `10-12`), וכו', וכו'. הקפיצות הכלולות בסוגריים נחשבות למהלך אחד, מכיוון שהן נעשות עם אותו אסימון. מצא את המספר המועט ביותר של מהלכים אפשריים. כמובן שאסורות קפיצות אלכסוניות; אתה יכול לקפוץ רק בכיוון הקווים.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 227
-
עשרת התפוחים
 המשפחה המיוצגת באיור משעשעת את עצמה עם החידה הקטנה הזו, שהיא לא מאוד קשה אבל די מעניינת. כפי שניתן לראות, הם הניחו שש עשרה צלחות על השולחן בצורת ריבוע, ושמו תפוח בכל אחת מעשר צלחות. הם רוצים למצוא דרך להסיר את כל התפוחים מלבד אחד על ידי קפיצה מעל אחד בכל פעם לריבוע הפנוי הבא, כמו בדמקה; או, יותר נכון, כמו בסוליטר, כי אסור לבצע מהלכים אלכסוניים - רק מהלכים מקבילים לצדדי הריבוע. ברור שעם מיקום התפוחים הנוכחי, לא ניתן לבצע אף מהלך, אבל מותר להעביר כל תפוח בודד שתרצו לצלחת ריקה לפני שמתחילים. לאחר מכן, כל המהלכים חייבים להיות קפיצות, תוך הסרת התפוחים שקופצים מעליהם.
מקורות:נושאים:חידות ורבוסים
המשפחה המיוצגת באיור משעשעת את עצמה עם החידה הקטנה הזו, שהיא לא מאוד קשה אבל די מעניינת. כפי שניתן לראות, הם הניחו שש עשרה צלחות על השולחן בצורת ריבוע, ושמו תפוח בכל אחת מעשר צלחות. הם רוצים למצוא דרך להסיר את כל התפוחים מלבד אחד על ידי קפיצה מעל אחד בכל פעם לריבוע הפנוי הבא, כמו בדמקה; או, יותר נכון, כמו בסוליטר, כי אסור לבצע מהלכים אלכסוניים - רק מהלכים מקבילים לצדדי הריבוע. ברור שעם מיקום התפוחים הנוכחי, לא ניתן לבצע אף מהלך, אבל מותר להעביר כל תפוח בודד שתרצו לצלחת ריקה לפני שמתחילים. לאחר מכן, כל המהלכים חייבים להיות קפיצות, תוך הסרת התפוחים שקופצים מעליהם.
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 228
-
תשעת השקדים
"הנה חידה קטנה," אמר כומר, "שמצאתי אותה מרתקת במיוחד. היא כל כך פשוטה, ובכל זאת היא משאירה אותך מעוניין ללא הגבלת זמן."
הכומר הנכבד לקח דף נייר וחילק אותו לעשרים וחמישה ריבועים, כמו חלק מרובע של לוח שחמט. אחר כך הניח תשעה שקדים על הריבועים המרכזיים, כפי שמוצג באיור, שם ייצגנו דלפקים ממוספרים לנוחיות במתן הפתרון.
"עכשיו, החידה היא," המשיך הכומר, "להסיר שמונה מהשקדים ולהשאיר את התשיעי בריבוע המרכזי. אתה מבצע את ההסרות על ידי קפיצה של שקד אחד מעל שקד אחר לריבוע הריק שמעבר והסרת זה שקפצו מעליו—בדיוק כמו בדמקה, רק כאן אתה יכול לקפוץ לכל כיוון, ולא רק באלכסון. העניין הוא לעשות את זה במספר המהלכים המועט ביותר האפשרי."
ניסיון הדגמה הבא יבהיר הכל. קפוץ `4` מעל `1, 5` מעל `9, 3` מעל `6, 5` מעל `3, 7` מעל `5` ו-`2, 4` מעל `7, 8` מעל `4`. אבל `8` לא נשאר בריבוע המרכזי, כפי שהוא צריך להיות. זכור להסיר את אלה שאתה קופץ מעליהם. כל מספר של קפיצות ברציפות עם אותו שקד נחשב למהלך אחד.
מקורות: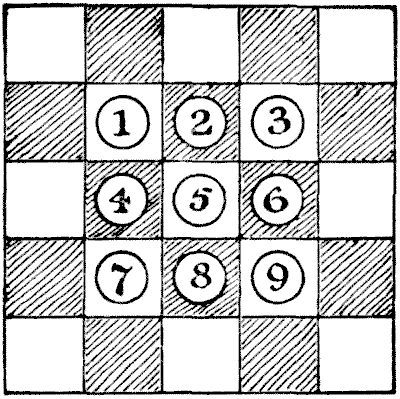
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 229