חידות ורבוסים

זוהי קטגוריה כללית לחידות מחשבה הדורשות פיקחות, חשיבה יצירתית או זיהוי תבניות. רבוסים הם חידות מילים המשתמשות בתמונות, סמלים או אותיות לייצוג מילים או ביטויים. גרסאות הקשורות למתמטיקה עשויות לכלול רמזים מספריים או תפעוליים המוסתרים בפורמט חזותי.

חידות גפרורים שחזרו את התרגיל

  • סוליטר לוח שחמט

    הנה הרחבה של משחק הסוליטר האחרון. כל מה שאתם צריכים זה לוח שחמט ושלושים ושניים כלים, או אותו מספר של דמקה או חיילים. באיור נעשה שימוש בחיילים ממוספרים. החידה היא להסיר את כל החיילים חוץ משניים, ושני אלה חייבים להיות במקור באותו צד של הלוח; כלומר, שני הנותרים חייבים להיות שייכים לקבוצה `1` עד `16` או לקבוצה השנייה, `17` עד `32`. מסירים חייל על ידי קפיצה מעליו עם חייל אחר למשבצת הבאה מעבר לו, אם המשבצת הזו פנויה, אבל אי אפשר לבצע קפיצה בכיוון אלכסוני. המהלכים הבאים יבהירו את המשחק: `3-11`, `4-12`, `3-4`, `13-3`. כאן `3` קופץ מעל `11`, ואתם מסירים את `11`; `4` קופץ מעל `12`, ואתם מסירים את `12`; וכן הלאה. יתגלה שזהו משחק סבלנות קטן ומרתק, והפתרון דורש הפעלת תושייה מסוימת. מקורות:

  • המפלצת

    בערב חג מולד אחד נסעתי ברכבת למקום קטן באחד המחוזות הדרומיים. התא היה מלא מאוד, והנוסעים היו דחוסים מאוד. השכן שלי באחד ממושבי הפינה למד בקפידה עמדה שהוצבה על אחד מלוחות השחמט המתקפלים הקטנים שאפשר לשאת בנוחות בכיס, ובקושי יכולתי להימנע מלהסתכל בו בעצמי. הנה העמדה:— 

     

    חברי הנוסע סובב לפתע את ראשו ותפס את מבט התימהון על פני.

    "אתה משחק שחמט?" הוא שאל.

    "כן, קצת. מה זה? בעיה?"

    "בעיה? לא; משחק."

    "בלתי אפשרי!" קראתי בגסות למדי. "העמדה היא מפלצת מושלמת!"

    הוא הוציא מכיסו גלויה ומסר לי אותה. היה כתוב בצד אחד כתובת ובצד השני המילים "`43`. K to Kt `8`."

    "זה משחק בהתכתבות." הוא קרא. "זה המהלך האחרון של חברי, ואני שוקל את תגובתי."

    "אבל אתה באמת חייב לסלוח לי; העמדה נראית בלתי אפשרית לחלוטין. איך לעזאזל, למשל—"

    "אה!" הוא קטע בחיוך. "אני רואה; אתה מתחיל; אתה משחק כדי לנצח."

    "כמובן שלא היית משחק כדי להפסיד או לסיים בתיקו!"

    הוא צחק בקול רם."יש לך הרבה מה ללמוד. אני וחברי לא משחקים בשביל תוצאות מהסוג המיושן הזה. אנו מחפשים בשחמט את הנפלא, את ההגחמתי, את המוזר. האם ראית אי פעם עמדה כזו?"

    ברכתי את עצמי בליבי שמעולם לא ראיתי.

    "העמדה הזו, אדוני, מממשת את ההתפתחויות המתפתלות ואת השרשורים הסינקרטיים, הסינתטיים והסינכרוניים של שתי אינדיבידואליות מוחיות. זהו תוצר של חילופי אמפוטריים ואינטרקלטוריים של—"

    "האם ראית את עיתון הערב, אדוני?" קטע האיש שממול, והושיט עיתון. שמתי לב בשוליים ליד האגודל שלו לכמה כתובים בעיפרון. בהודייה לו, לקחתי את העיתון וקראתי—"משוגע, אבל די לא מזיק. הוא באחריותי."

    אחרי זה נתתי לבחור המסכן להמשיך בדרכו הפרועה עד ששניהם ירדו בתחנה הבאה.

    אבל העמדה המוזרה הזו התקבעה בזיכרוני בצורה בלתי ניתנת למחיקה, עם המהלך האחרון של השחור `43`. K to Kt `8`; וזמן קצר לאחר מכן מצאתי שאפשר להגיע לעמדה כזו בארבעים ושלושה מהלכים. האם הקורא יכול לבנות רצף כזה? איך הלבן הכניס את הצריחים והרץ של המלך שלו לעמדות הנוכחיות שלהם, בהתחשב בכך שהשחור מעולם לא הזיז את הרץ של המלך שלו? לא ניתנו יתרונות, וכל מהלך היה לגיטימי לחלוטין.

    מקורות:

  • ארבע הבריחות

    קולונל ב—— היה אלמן בעל מזג שתקני מאוד. יחסו לארבע בנותיו היה חמור בצורה יוצאת דופן, כמעט אכזרי, והן באופן טבעי חשו נטייה להתרעם על כך. בהיותן נערות מקסימות בעלות כל מידה טובה והישגים רבים, אין זה מפתיע שלכל אחת היה מעריץ נלהב. אבל האב אסר על הצעירים לבקר בביתו, יירט את כל המכתבים והעמיד את בנותיו תחת פיקוח הדוק יותר מאי פעם. אבל האהבה, שלועגת למנעולים, מפתחות וחומות גן, הייתה שווה למקרה, וארבעת הצעירים קשרו קשר ותכננו בריחה כללית.

    למרגלות מדשאת הטניס בתחתית הגן זרם נהר התמזה הכסוף, ובלילה אחד, לאחר שארבע הבנות הוצאו בבטחה מחלון מעונות ל-terra firma, הן התגנבו בשקט אל גדת הנהר, שם עגנה סירה קטנה השייכת לקולונל. בעזרת זאת הם הציעו לחצות לצד הנגדי ולעשות את דרכם לסמטה שבה חיכו כלי רכב שיישאו אותם במנוסתם. אבוי! כאן, על שפת המים, החלו כבר קשייהם.

    הצעירים היו כה קנאים, שאף אחד מהם לא הרשה לארוסתו העתידית להישאר בכל עת בחברת גבר אחר, או גברים, אלא אם כן הוא עצמו נכח גם כן. כעת, הסירה יכלה להכיל רק שני אנשים, אם כי כמובן שאפשר היה לחתור בה על ידי אדם אחד, ונראה היה שאי אפשר לארבעת הזוגות לחצות אי פעם. אבל באמצע הזרם היה אי קטן, ונראה היה שהוא מציג מוצא מהקושי, משום שאפשר היה להשאיר שם אדם או אנשים בזמן שהסירה חתרה חזרה או אל הגדה הנגדית. אילו היו ערוכים לקושי שלהם, הם יכלו למצוא בקלות פתרון לבעיה הקטנה הזו בכל זמן אחר. אבל הם היו עכשיו כה ממהרים ונרגשים במנוסתם, שהבלבול שאליו נקלעו עד מהרה היה משעשע ביותר—או שהיה יכול להיות לכל אחד מלבדם.

    כתוצאה מכך, הם לקחו פי שניים זמן וחצו את הנהר פי שניים בתדירות גבוהה מהדרוש. בינתיים, הקולונל, שהיה ישן קל מאוד, חשב ששמע התזה של משוטים. הוא העלה במהירות את האזעקה בקרב בני ביתו, ונמצא שהנערות נעדרות. מישהו נשלח לתחנת המשטרה, ומספר שוטרים סייעו עד מהרה במרדף אחר הבורחים, אשר, כתוצאה מהעיכוב הזה בחציית הנהר, נתפסו במהירות. ארבע הבנות חזרו בעצב לבתיהן, ולאחר מכן ניתקו את אירוסיהן בתיעוב.

    במשך זמן רב היה זה תעלומה כיצד הצליחה קבוצת שמונת האנשים לחצות את הנהר בסירה הקטנה ההיא מבלי שאף נערה תישאר אי פעם עם גבר, אלא אם כן גם ארוסה היה נוכח. השיטה המועדפת היא לקחת שמונה אסימונים או פיסות קרטון ולסמן אותם A, B, C, D, a, b, c, d, כדי לייצג את ארבעת הגברים ואת הכלות העתידיות שלהם, ולשאת אותם מצד אחד של שולחן למשנהו בקופסת גפרורים (כדי לייצג את הסירה), כאשר מטבע מוצב באמצע השולחן כאי.

    קוראים מתבקשים כעת למצוא את השיטה המהירה ביותר להעברת המשתתפים מעבר לנהר. כמה מעברים נחוצים מיבשה ליבשה? על ידי "יבשה" מובן או חוף או אי. למרות שהסירה לא בהכרח תעגון באי בכל פעם של חציה, יש להיערך לאפשרות שזה יקרה. לדוגמה, לא יתאים שגבר יהיה לבדו בסירה (אף שהובן שהוא התכוון רק לחצות מגדה אחת לגדה הנגדית) אם במקרה הייתה נערה לבדה על האי מלבד זו שאליה היה מאורס.

    מקורות:

  • חידת קלף ה-"T"

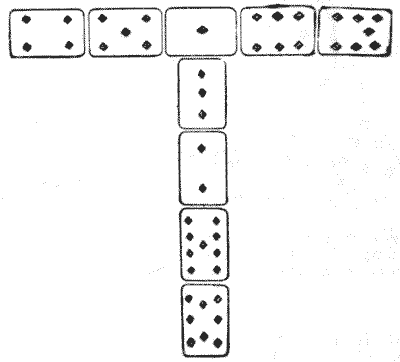    חידה משעשעת עם קלפים היא לקחת את תשעת הקלפים מסדרה אחת, מאס ועד תשע כולל, ולסדר אותם בצורת האות "T," כפי שמוצג באיור, כך שהנקודות בשורה האופקית יספרו אותו דבר כמו אלו בעמודה. בדוגמה הנתונה הם מסתכמים לעשרים ושלוש בשני הכיוונים. עכשיו, זה די קל להשיג סידור נכון יחיד. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת. למרות שהמספר גבוה, הפתרון לא באמת קשה אם נתקוף את החידה בצורה הנכונה. את הדרך ההפוכה המתקבלת על ידי שיקוף האיור במראה לא נספור כשונה, אך כל שאר השינויים במיקומים היחסיים של הקלפים ייספרו כאן. כמה דרכים שונות יש? מקורות:

  • "STRAND" סבלנות

    הרעיון לכך עלה לי כששקלתי את משחק הסבלנות שנתתי בתוך Strand Magazine לחודש דצמבר, `1910`, אשר הודפס מחדש בספרו השני של ארנסט ברגהולט Second Book of Patience Games, תחת השם החדש "המלך אלברט".

    צרו שתי ערימות קלפים באופן הבא: `9` יהלום, `8` עלה, `7` יהלום, `6` עלה, `5` יהלום, `4` עלה, `3` יהלום, `2` עלה, `1` יהלום, ו-`9` תלתן, `8` תלתן, `7` תלתן, `6` תלתן, `5` תלתן, `4` תלתן, `3` תלתן, `2` תלתן, `1` תלתן, כאשר ה-`9` של יהלומים בתחתית ערימה אחת וה-`9` של תלתן בתחתית הערימה האחרת. המטרה היא להחליף את העלים עם התלתנים, כך שהיהלומים והתלתנים עדיין יהיו בסדר מספרי בערימה אחת והתלתנים והעלים בערימה השנייה. ישנם ארבעה מקומות פנויים בנוסף לשני המקומות שתפוסים על ידי הערימות, וניתן להניח כל קלף על מקום פנוי, אבל ניתן להניח קלף רק על קלף אחר בעל ערך גבוה יותר הבא אחריו — אס על שתיים, שתיים על שלוש וכן הלאה. נדרשת סבלנות כדי לגלות את הדרך הקצרה ביותר לעשות זאת. כאשר ישנם ארבעה מקומות פנויים, ניתן לערום ארבעה קלפים בשבעה מהלכים, עם שלושה מקומות בלבד ניתן לערום אותם בתשעה מהלכים, ועם שני מקומות אי אפשר לערום יותר משני קלפים. כאשר יש לך תפיסה של עובדות אלה ודומות להן, תוכל להסיר מספר קלפים בשלמותם ולרשום `7, 9`, או כל מספר המהלכים הנדרש. הקיצור ההדרגתי של המשחק הוא מרתק, והניסיונות הראשונים הם ארוכים באופן מפתיע.

    מקורות:

  • רצועות הקסם

     

    קרה שהיו מונחות על השולחן שלי מספר רצועות קרטון, ועליהן מודפסים מספרים מ-`1` ומעלה בסדר עולה. עלה בי הרעיון לפתע, כפי שלרעיונות יש נטייה להופיע באופן בלתי צפוי, ליצור חידה קטנה. אני תוהה אם קוראים רבים יגיעו לאותו פתרון שאני הגעתי אליו.

    קחו שבע רצועות קרטון והניחו אותן יחד כפי שמוצג לעיל. לאחר מכן כתבו על כל אחת מהן את המספרים `1, 2, 3, 4, 5, 6, 7`, כפי שמוצג, כך שהמספרים ייצרו שבע שורות ושבע עמודות.

    כעת, החידה היא לחתוך את הרצועות הללו למספר המועט ביותר של חלקים, כך שניתן יהיה להניח אותם יחד וליצור ריבוע קסם, כאשר שבע השורות, שבע העמודות ושני האלכסונים מסתכמים לאותו מספר. אסור להפוך או להניח אף ספרה על צידה — כלומר, כל הרצועות חייבות להיות מונחות בכיוון המקורי שלהן.

    כמובן שאפשר לחתוך כל רצועה לשבעה חלקים נפרדים, כאשר כל חלק מכיל מספר, והחידה תהיה קלה מאוד, אבל אני לא צריך לומר שארבעים ותשעה חלקים רחוקים מאוד מלהיות המספר המועט ביותר האפשרי.

    מקורות:

  • שמונה אסירים עליזים

     

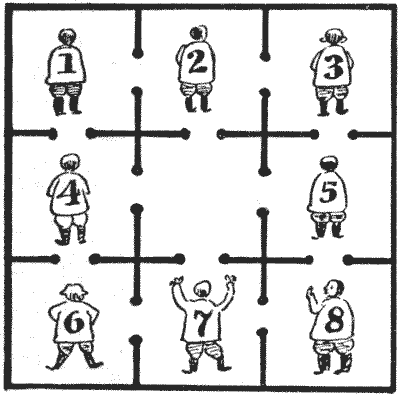
    האיור מציג תוכנית של בית סוהר המכיל תשעה תאים, כולם מקושרים זה לזה באמצעות פתחי דלתות. לשמונת האסירים יש מספרים על גבם, ומותר לכל אחד מהם להתעמל בכל תא שמתפנה, בכפוף לכלל שבאף זמן נתון לא יהיו שני אסירים באותו תא. המלך העליז שבתחום שלטונו היה ממוקם בית הסוהר הציע להם נוחיות מיוחדות בערב חג המולד אחד, אם, מבלי להפר את הכלל הזה, הם יוכלו למקם את עצמם כך שמספריהם ייצרו ריבוע קסם.

    כעת, לאסיר מספר `7` היה ידע רב על ריבועי קסם, ולכן הוא פיתח תוכנית ובחר באופן טבעי בשיטה המהירה ביותר—כלומר, כזו הכוללת את המספר הקטן ביותר האפשרי של מעברים מתא לתא. אבל אחד האנשים היה ממורמר, עקשן (בלתי מתאים לחלוטין לחברתם של חבריו העליזים), והוא סירב לצאת מתאו או לקחת חלק כלשהו בהליכים. אבל מספר `7` היה שווה ערך לחלוטין למצב החירום, וגילה שהוא עדיין יכול לעשות את מה שנדרש במספר המועט ביותר האפשרי של מהלכים, מבלי להטריד את הבהמה לעזוב את תאו. החידה היא להראות איך הוא עשה זאת, ואגב כך, לגלות איזה אסיר היה טיפש ועקשן כל כך. האם תוכלו למצוא את הבחור?

    מקורות:

  • שמונה עשרה אבני דומינו

    האיור מציג שמונה עשרה אבני דומינו המסודרות בצורת ריבוע, כך שמספר הנקודות בכל אחד מששת הטורים, שש השורות ושני האלכסונים הארוכים מסתכם ל-`13`. זהו הסכום הקטן ביותר האפשרי עם מבחר כלשהו של אבני דומינו מקופסה רגילה של עשרים ושמונה. הסכום הגדול ביותר האפשרי הוא `23`, ופתרון למספר זה ניתן להשיג בקלות על ידי החלפת כל מספר במשלים שלו ל-`6`. לכן, עבור כל ריבוע ריק, החליפו `6`, עבור כל `1` החליפו `5`, עבור כל `2` החליפו `4`, עבור `3` החליפו `3`, עבור `4` החליפו `2`, עבור `5` החליפו `1`, ועבור `6` החליפו ריבוע ריק. אבל החידה היא לבצע בחירה של שמונה עשרה אבני דומינו ולסדר אותן (בדיוק בצורה המוצגת) כך שהסכומים יהיו `18` בכל ארבעה עשר הכיוונים שהוזכרו.

    מקורות:

  • החידה בצורת "T" של המנדרין

     

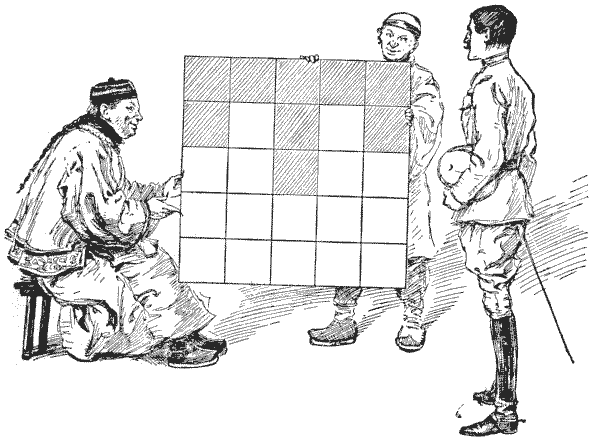
    לפני שמארג׳וריבנקס בושאמפ צ׳ולמונדלי יצא לסיורו במזרח הרחוק, הוא התגאה בידע שלו בריבועים קסומים, נושא שהפך לתחביב מיוחד שלו; אבל עד מהרה הוא גילה שמעולם לא נגע יותר מאשר בשולי הנושא, ושצ׳יני ערמומי יכול לנצח אותו בקלות. אני מציג בעיה קטנה שמנדרין מלומד הציג למטייל שלנו, כפי שמצויר בעמוד האחרון.

    הסיני, לאחר שהעיר שהבנייה של ריבוע קסם רגיל של עשרים וחמישה תאים היא "too velly muchee easy," ביקש מבן ארצנו למקם את המספרים `1` עד `25` בריבוע כך שכל עמודה, כל שורה וכל אחד משני האלכסונים יסתכמו ל-`65`, כאשר רק מספרים ראשוניים נמצאים על ה-"T" המוצלל. כמובן שהמספרים הראשוניים הזמינים הם `1, 2, 3, 5, 7, 11, 13, 17, 19`, ו-`23`, כך שיש לך חופש לבחור כל תשעה מהם שישרתו את מטרתך. האם אתה יכול לבנות את ריבוע הקסם הקטן והסקרן הזה?

    מקורות:

  • חידת השבת

    נתקלתי בחידה קטנה זו בספר ישן. אני תוהה כמה קוראים יראו את הפתרון שהמחבר התכוון אליו. 

    הנוצרים את היום הראשון בשבוע כשבת יחזיקו;
    היהודים את השביעי, כפי שעשו מקדמת דנא;
    הטורקים את השישי, כפי שנאמר לנו לעתים קרובות.
    כיצד יכולים שלושתם, באותו מקום ויום,
    שלכל אחד תהיה השבת האמיתית שלו? אמור, אני מתפלל.

    מקורות: