חידות ורבוסים
זוהי קטגוריה כללית לחידות מחשבה הדורשות פיקחות, חשיבה יצירתית או זיהוי תבניות. רבוסים הם חידות מילים המשתמשות בתמונות, סמלים או אותיות לייצוג מילים או ביטויים. גרסאות הקשורות למתמטיקה עשויות לכלול רמזים מספריים או תפעוליים המוסתרים בפורמט חזותי.
חידות גפרורים שחזרו את התרגיל-
חידת יתדות הכובעים
הנה חידה בת חמש מלכות שהצגתי בצורה דמיונית בשנת `1897`. מכיוון שהמלכות יוצגו שם ככובעים על שישים וארבעה יתדות, אדבוק בכותרת, "חידת יתדות הכובעים". ניתן לראות שכל משבצת מאוכלסת או מותקפת. החידה היא להעביר מלכה אחת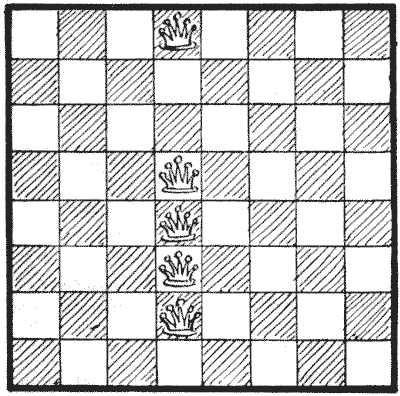 למשבצת אחרת כך שעדיין כל משבצת תהיה מאוכלסת או מותקפת, לאחר מכן להעביר מלכה שנייה בתנאים דומים, לאחר מכן מלכה שלישית, ולבסוף מלכה רביעית. לאחר המסע הרביעי כל משבצת חייבת להיות מותקפת או מאוכלסת, אך אף מלכה לא תתקוף מלכה אחרת. כמובן, שהמסעים לא חייבים להיות "מסעי מלכה"; ניתן להעביר מלכה לכל חלק בלוח.
מקורות:
למשבצת אחרת כך שעדיין כל משבצת תהיה מאוכלסת או מותקפת, לאחר מכן להעביר מלכה שנייה בתנאים דומים, לאחר מכן מלכה שלישית, ולבסוף מלכה רביעית. לאחר המסע הרביעי כל משבצת חייבת להיות מותקפת או מאוכלסת, אך אף מלכה לא תתקוף מלכה אחרת. כמובן, שהמסעים לא חייבים להיות "מסעי מלכה"; ניתן להעביר מלכה לכל חלק בלוח.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 315
-
האמזונות
 חידה זו מבוססת על חידה של קפטן טורטון. הסירו שלוש מלכות לריבועים אחרים כך שיישארו אחד-עשר ריבועים על הלוח שאינם מותקפים. הסרת שלוש המלכות אינה צריכה להתבצע על ידי "מהלכי מלכה". אתם יכולים פשוט להרים אותן ולהניח אותן בכל מקום. יש רק פתרון אחד.
מקורות:נושאים:חידות ורבוסים
חידה זו מבוססת על חידה של קפטן טורטון. הסירו שלוש מלכות לריבועים אחרים כך שיישארו אחד-עשר ריבועים על הלוח שאינם מותקפים. הסרת שלוש המלכות אינה צריכה להתבצע על ידי "מהלכי מלכה". אתם יכולים פשוט להרים אותן ולהניח אותן בכל מקום. יש רק פתרון אחד.
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 316
-
מסע הצריח
אני קורא לחידה הזו "מסע הצריח", מכיוון שהמילה "tour" (הנגזרת מגלגל של חרט) מרמזת שאנו חוזרים לנקודה ממנה יצאנו, ואנו לא עושים זאת במקרה הזה. לא נהיה מרוצים מסיור חג מודרך אישית שהסתיים בכך שהשאיר אותנו, למשל, באמצע הסהרה. הצריח כאן עושה עשרים ואחד מהלכים, שבמהלכם הוא מבקר בכל משבצת בלוח פעם אחת בלבד, ועוצר במשבצת המסומנת `10` בסוף המהלך העשירי שלו, ומסתיים במשבצת המסומנת `21`. שני מהלכים רצופים אינם יכולים להתבצע באותו כיוון - כלומר, עליך לבצע פנייה לאחר כל מהלך.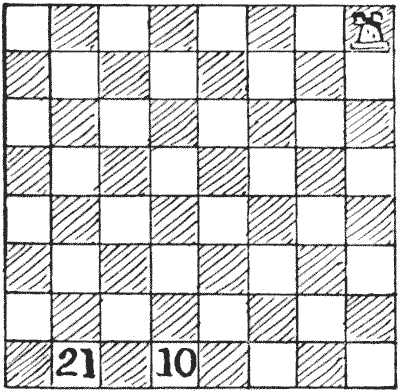 מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 321
-
ביקור אפיסקופלי
המשבצות הלבנות על לוח השחמט מייצגות את הקהילות של דיוקסיה. הניחו את הרץ על כל משבצת שתרצו, ותכננו כך ש (תוך שימוש בתנועת הרץ הרגילה בשחמט) הוא יבקר בכל אחת מהקהילות שלו במספר המהלכים המועט ביותר האפשרי. כמובן, כל הקהילות שעוברים דרכן בכל מהלך נחשבות כ"ביקורות". אתם יכולים לבקר בכל משבצת יותר מפעם אחת, אך אסור לכם לנוע פעמיים בין אותן שתי משבצות סמוכות. מהו מספר המהלכים המועט ביותר האפשרי? הרץ לא צריך לסיים את ביקורו בקהילה ממנה יצא לדרך לראשונה.מקורות:נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> תורת המשחקים קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 325
-
חידת מונה חדשה
הנה חידה חדשה עם הזזת מונים, או מטבעות, שמבט ראשון נראית כאילו היא פשוטה באופן אבסורדי. אבל יתברר שהיא מעט מבלבלת. אני מציג אותה כאן מסיבה שאסביר כשאגיע לחידה הבאה. העתק את הדיאגרמה הפשוטה, מוגדלת, על דף נייר; ואז הנח שני מונים לבנים על הנקודות `1` ו-`2`, ושני מונים אדומים על `9` ו-`10`. החידה היא לגרום לאדומים ולבנים להחליף מקומות. אתה רשאי להזיז את המונים אחד בכל פעם בכל סדר שתרצה, לאורך הקווים מנקודה לנקודה, עם ההגבלה היחידה שמונה אדום ולבן לעולם לא יעמדו בבת אחת על אותו קו ישר. לכן המהלך הראשון יכול להיות רק מ-`1` או `2` ל-`3`, או מ-`9` או `10` ל-`7`.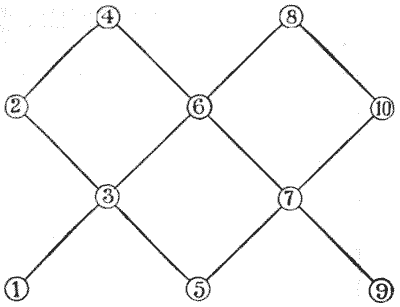 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 326
-
החידה החדשה של הרץ

זוהי חידה קטנה ומסקרנת למדי. הניחו שמונה רצים (ארבעה שחורים וארבעה לבנים) על לוח השחמט המצומצם, כפי שמוצג באיור. הבעיה היא לגרום לרצים השחורים להחליף מקומות עם הלבנים, כך שאף רץ לא יתקוף רץ אחר מצבע מנוגד. הם חייבים לנוע לחלופין—תחילה רץ לבן, אחר כך רץ שחור, אחר כך רץ לבן, וכן הלאה. כאשר תצליחו לעשות זאת בכלל, נסו למצוא את מספר המהלכים המינימלי האפשרי.
אם תוציאו את הרצים שעומדים על משבצות שחורות, ותשחקו רק על המשבצות הלבנות, תגלו שהחידה האחרונה שלי הסתובבה על צידה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 327
-
סיור המלכה
החידה של ביצוע סיור שלם בלוח השחמט עם המלכה במספר המהלכים המועט ביותר האפשרי (שבו ניתן לבקר בריבועים יותר מפעם אחת) ניתנה לראשונה על ידי סם לויד המנוח ב-אסטרטגיית שחמט שלו. אבל הפתרון המוצג להלן הוא זה שהוא נתן ב-אגוזי שחמט אמריקאים ב-`1868`. תיעדתי לפחות שישה פתרונות שונים במספר המינימלי של מהלכים - ארבעה עשר - אבל זה הטוב מכולם, מסיבות שאסביר.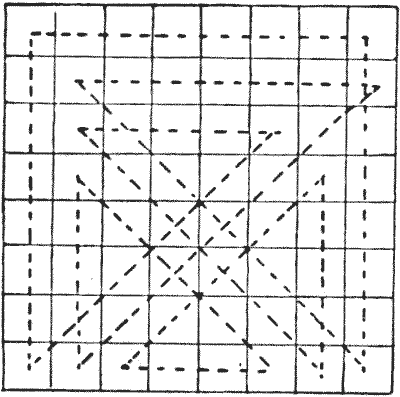 אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: -
אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: - 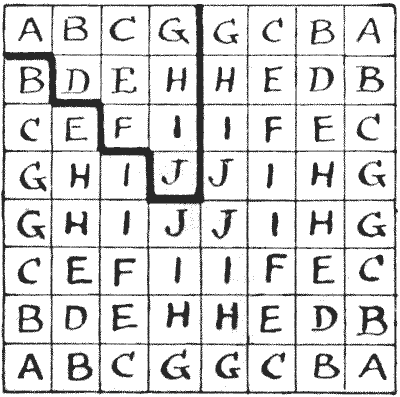 התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת המשחקים קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים
התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת המשחקים קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 328
-
פאזל הכוכבים

הניחו את חוד העיפרון שלכם על אחד הכוכבים הלבנים ו(מבלי להרים את העיפרון מהדף) מחקו את כל הכוכבים בארבעה עשר קווים ישרים רציפים, כשאתם מסיימים בכוכב הלבן השני. הקווים הישרים שלכם יכולים להיות בכל כיוון שתרצו, רק כל פנייה חייבת להתבצע על כוכב. אין התנגדות למחוק כוכב כלשהו יותר מפעם אחת.
במקרה הזה, כאשר ריבועי ההתחלה והסיום שלכם מקובעים בצורה לא נוחה, אינכם יכולים להשיג פתרון על ידי שבירת מסע מלכה, או בכל דרך אחרת באמצעות מסעי מלכה בלבד. אבל מותר לכם להשתמש בקווים ישרים אלכסוניים —כגון מהכוכב הלבן העליון ישירות לכוכב פינתי.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 329
-
המחליקן המדעי

ניתן לראות שהמחליקן סימן על הקרח שישים וארבע נקודות או כוכבים, והוא מציע להתחיל מהמיקום הנוכחי שלו ליד הפינה ולהיכנס לכל אחת מהנקודות בארבעה עשר קווים ישרים. איך הוא יעשה זאת? כמובן שאין התנגדות לכך שהוא יעבור על פני כל נקודה יותר מפעם אחת, אבל המהלך הישר האחרון שלו חייב להחזיר אותו למיקום שממנו הוא התחיל.
זה רק עניין של לקחת את העיפרון ולהתחיל מהמקום שבו רגלו של המחליקן נחה כרגע, ולמחוק את כל הכוכבים בארבעה עשר קווים ישרים רצופים, ולחזור לנקודה ממנה יצאתם.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 331
-
מסעה של המלכה
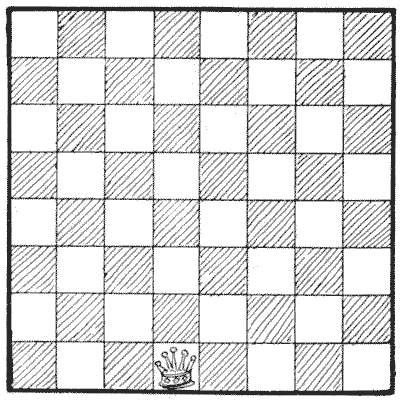 הניחו את המלכה על המשבצת שלה, כפי שמוצג באיור, ואז נסו לגלות את המרחק הגדול ביותר שהיא יכולה לעבור על הלוח בחמישה מהלכי מלכה מבלי לעבור על אף משבצת בפעם השנייה. סמנו את נתיב המלכה על הלוח, ושימו לב היטב גם לכך שאסור לה לחצות את המסלול שלה. זה נראה פשוט מספיק, אבל הקורא עשוי לגלות שהוא נכשל.
מקורות:
הניחו את המלכה על המשבצת שלה, כפי שמוצג באיור, ואז נסו לגלות את המרחק הגדול ביותר שהיא יכולה לעבור על הלוח בחמישה מהלכי מלכה מבלי לעבור על אף משבצת בפעם השנייה. סמנו את נתיב המלכה על הלוח, ושימו לב היטב גם לכך שאסור לה לחצות את המסלול שלה. זה נראה פשוט מספיק, אבל הקורא עשוי לגלות שהוא נכשל.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 333