חידות ורבוסים
זוהי קטגוריה כללית לחידות מחשבה הדורשות פיקחות, חשיבה יצירתית או זיהוי תבניות. רבוסים הם חידות מילים המשתמשות בתמונות, סמלים או אותיות לייצוג מילים או ביטויים. גרסאות הקשורות למתמטיקה עשויות לכלול רמזים מספריים או תפעוליים המוסתרים בפורמט חזותי.
חידות גפרורים שחזרו את התרגיל-
תעלומת שנים-עשר הפני
הנה חידה נחמדה וקטנה הדורשת רק שנים-עשר פני או אסימונים. סדרו אותם במעגל, כפי שמוצג באיור. כעת הרימו פני אחד בכל פעם, והעבירו אותו מעל שני פני, והניחו אותו על הפני השלישי. לאחר מכן הרימו פני בודד נוסף ועשו את אותו הדבר, וכן הלאה, עד שבשישה מהלכים כאלה, יהיו לכם המטבעות בשישה זוגות בעמדות `1, 2, 3, 4, 5, 6`. אתם יכולים לנוע בכל כיוון סביב המעגל בכל מהלך, וזה לא משנה אם השניים שקפצתם מעליהם מופרדים או זוג. זה די קל אם אתם משתמשים רק במעט מחשבה.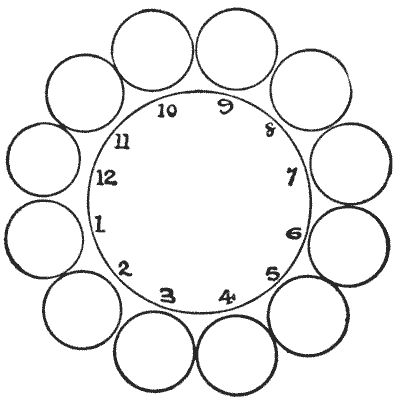 מקורות:נושאים:חידות ורבוסים
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 230
-
צלחות ומטבעות
הנח שתים עשרה צלחות, כפי שמוצג, על שולחן עגול, עם מטבע או תפוז בכל צלחת. התחל מכל צלחת שתרצה, ותמיד בכיוון אחד סביב השולחן, קח מטבע אחד, העבר אותו מעל שני מטבעות אחרים והנח אותו בצלחת הבאה. המשך שוב; קח מטבע נוסף, ולאחר שהעברת אותו מעל שני מטבעות, הנח אותו בצלחת; וכך המשך במסעך. יש להסיר שישה מטבעות בלבד, וכאשר אלה הונחו, צריכים להיות שני מטבעות בכל אחת משש צלחות ושש צלחות ריקות. נקודה חשובה בחידה היא להקיף את השולחן כמה שפחות פעמים. לא משנה אם שני המטבעות שעליהם עוברים נמצאים בצלחת אחת או בשתי צלחות, וגם לא כמה צלחות ריקות מעבירים מטבע מעליהן. אבל אתה חייב תמיד ללכת בכיוון אחד סביב השולחן ולסיים בנקודה ממנה יצאת. היד שלך, כלומר, מתקדמת בהתמדה בכיוון אחד, מבלי לזוז אחורה. מקורות:נושאים:חידות ורבוסים
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 231
-
המוכר גבינות האקסצנטרי
 מוכר הגבינות המתואר באיור הוא חובב חידות מושבע. אחת החידות האהובות עליו היא ערימת גבינות במחסן שלו, שעשוע שהוא מוצא בו פעילות גופנית טובה כמו גם תרגול מחשבתי. הוא מניח שש עשרה גבינות על הרצפה בשורה ישרה ואז הופך אותן לארבע ערימות, עם ארבע גבינות בכל ערימה, על ידי העברת גבינה מעל ארבע אחרות. אם תשתמשו בשש עשרה אסימונים ותמספרו אותם בסדר מ-`1` עד `16`, תוכלו להניח את `1` על `6, 11` את `7` על `4`, וכן הלאה, עד שיהיו ארבעה בכל ערימה. ניתן לראות שזה לא משנה אם ארבעת אלה שמעבירים מעליהם עומדים לבד או בערימה; הם נספרים בדיוק אותו הדבר, ותמיד אפשר לשאת גבינה לכל כיוון. ישנן דרכים רבות ושונות לעשות זאת בשנים עשר מהלכים, כך שזה הופך למשחק טוב של "סבלנות" לנסות לפתור אותו כך שארבע הערימות יישארו במקומות מותנים שונים. לדוגמה, נסו להשאיר את הערימות בקצוות הקיצוניים של השורה, במספרים `1, 2, 15` ו-`16`; זה די קל. אחר כך נסו להשאיר שלוש ערימות יחד, במספרים `13, 14`, ו-`15`. שוב, שחקו כך שהן יישארו במספרים `3, 5, 12`, ו-`14`.
מקורות:נושאים:חידות ורבוסים
מוכר הגבינות המתואר באיור הוא חובב חידות מושבע. אחת החידות האהובות עליו היא ערימת גבינות במחסן שלו, שעשוע שהוא מוצא בו פעילות גופנית טובה כמו גם תרגול מחשבתי. הוא מניח שש עשרה גבינות על הרצפה בשורה ישרה ואז הופך אותן לארבע ערימות, עם ארבע גבינות בכל ערימה, על ידי העברת גבינה מעל ארבע אחרות. אם תשתמשו בשש עשרה אסימונים ותמספרו אותם בסדר מ-`1` עד `16`, תוכלו להניח את `1` על `6, 11` את `7` על `4`, וכן הלאה, עד שיהיו ארבעה בכל ערימה. ניתן לראות שזה לא משנה אם ארבעת אלה שמעבירים מעליהם עומדים לבד או בערימה; הם נספרים בדיוק אותו הדבר, ותמיד אפשר לשאת גבינה לכל כיוון. ישנן דרכים רבות ושונות לעשות זאת בשנים עשר מהלכים, כך שזה הופך למשחק טוב של "סבלנות" לנסות לפתור אותו כך שארבע הערימות יישארו במקומות מותנים שונים. לדוגמה, נסו להשאיר את הערימות בקצוות הקיצוניים של השורה, במספרים `1, 2, 15` ו-`16`; זה די קל. אחר כך נסו להשאיר שלוש ערימות יחד, במספרים `13, 14`, ו-`15`. שוב, שחקו כך שהן יישארו במספרים `3, 5, 12`, ו-`14`.
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 233
-
חידת ההחלפה
הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—
A B C D E F G H I J K L המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?
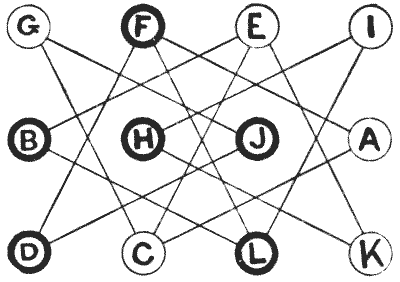
אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.
מקורות:נושאים:קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 234
-
חידת הכובעים
עשרה כובעים נתלו על יתדות כפי שמוצג באיור—חמישה כובעי משי וחמישה כובעי לבד, "בולרים," לסירוגין משי ולבד. שתי היתדות בקצה השורה היו ריקות.

החידה היא להסיר שני כובעים סמוכים אל היתדות הפנויות, לאחר מכן שני כובעים סמוכים אחרים אל היתדות שאינן מאוכלסות כעת, וכן הלאה עד שחמישה זוגות הועברו והכובעים שוב תלויים בשורה רציפה, אך עם כל כובעי המשי יחד וכל כובעי הלבד יחד.
זכרו, שני הכובעים המוסרים חייבים להיות תמיד סמוכים זה לזה, ועליכם לקחת אחד בכל יד ולהניח אותם על היתדות החדשות שלהם מבלי להפוך את מיקומם היחסי. אסור לכם לחצות את הידיים, וגם לא לתלות אחד בכל פעם.
האם תוכלו לפתור את החידה הישנה הזו, שאני נותן כמבוא לזו הבאה? נסו זאת עם אסימונים משני צבעים או עם מטבעות, וזכרו ששתי היתדות הריקות חייבות להישאר בקצה אחד של השורה.
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 236
-
בנים ובנות
אם תסמנו עשרה חלוקות על דף נייר כדי לייצג את הכיסאות, ותשתמשו בשמונה אסימונים ממוספרים עבור הילדים, יהיה לכם בילוי מרתק. תנו למספרים האי-זוגיים לייצג בנים ולמספרים הזוגיים בנות, או שתוכלו להשתמש באסימונים משני צבעים, או במטבעות.
החידה היא להסיר שני ילדים היושבים בכיסאות סמוכים ולהניח אותם בשני כיסאות ריקים, כאשר הם מחליפים צדדים תחילה; לאחר מכן הסירו זוג ילדים שני מכיסאות סמוכים והניחו אותם בשני הכיסאות הפנויים כעת, כשהם מחליפים צדדים; וכן הלאה, עד שכל הבנים יהיו ביחד וכל הבנות ביחד, כאשר שני הכיסאות הריקים בקצה אחד כמו עכשיו. כדי לפתור את החידה, עליכם לעשות זאת בחמישה מהלכים. שני הילדים חייבים תמיד להילקח מכיסאות הצמודים זה לזה; וזכרו את הנקודה החשובה של החלפת הצדדים בין שני הילדים, שכן זהו המאפיין הייחודי של החידה. על ידי "החלפת צדדים" אני פשוט מתכוון שאם, לדוגמה, תזיזו תחילה את `1` ו-`2` לכיסאות הריקים, אז הכיסא הראשון (החיצוני) יאוכלס על ידי `2` והשני על ידי `1`.
מקורות: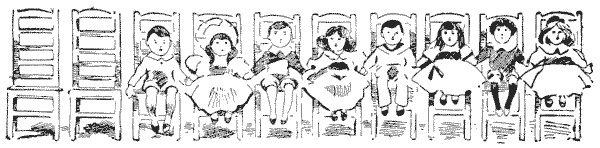
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 237
-
מסע האופניים
שני רוכבי אופניים התייעצו במפת דרכים לקראת טיול קצר משותף. העיגולים מייצגים ערים, וכל הדרכים הטובות מיוצגות על ידי קווים. הם מתחילים מהעיר עם הכוכב, ועליהם להשלים את הטיול שלהם ב-E. אבל לפני שהם מגיעים לשם הם רוצים לבקר בכל עיר אחרת פעם אחת, ורק פעם אחת. זו הבעיה. מר ספייסר אמר, "אני בטוח שנוכל למצוא דרך לעשות זאת;" אבל מר מגס השיב, "בשום אופן, אני בטוח." עכשיו, מי מהם צדק? קחו את העיפרון שלכם ובדקו אם תוכלו למצוא דרך לעשות זאת. כמובן שעליכם להישאר בדרכים המצוינות.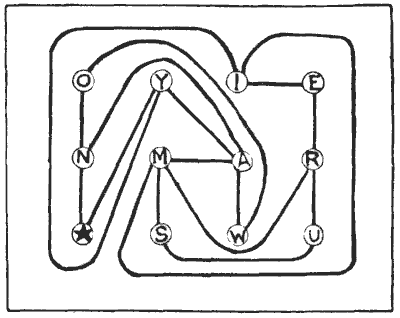 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 248
-
הטיול הגדול
אחת החידות היומיומיות של החיים היא תכנון מסלולים. אם אתם יוצאים לחופשה על אופניים, או לטיול מוטורי, תמיד עולה השאלה כיצד לנצל את הזמן והמשאבים שלכם בצורה הטובה ביותר. החלטתם להגיע למקום מסוים, לכלול ביקורים בעיר כזו וכזו, לנסות לראות משהו מעניין במיוחד במקום אחר, ואולי לנסות לבקר חבר ותיק בנקודה שלא תוציא אתכם בהרבה מהדרך. אז אתם צריכים לתכנן את המסלול שלכם כדי להימנע מכבישים גרועים, אזורים לא מעניינים, ואם אפשר, מהצורך לחזור באותה דרך שבה נסעתם. עם מפה לפניכם, ניגשים לפתרון החידה המעניינת. אציג לכם שאלה קטנה המבוססת על קווים אלה.
אני מציג מפה גסה של מדינה—אין צורך לומר איזו מדינה—העיגולים מייצגים ערים והקווים המקווקווים את מסילות הברזל המחברות ביניהן. עכשיו, בעיר המסומנת A חי אדם שנולד שם, ובמשך כל חייו מעולם לא עזב את מקום הולדתו. מנעוריו הוא היה חרוץ מאוד, דבק בעקביות במקצועו, ולא היה לו רצון לשוטט בחוץ. עם זאת, בהגיעו לגיל חמישים הוא החליט לראות קצת מהמדינה שלו, ובמיוחד לבקר חבר ותיק מאוד שגר בעיר המסומנת Z. מה שהוא הציע היה כזה: שהוא יתחיל מביתו, ייכנס לכל עיר פעם אחת בלבד, ויסיים את מסעו ב-Z. מכיוון שהוא החליט לבצע את הטיול הגדול הזה ברכבת בלבד, הוא התקשה קצת לתכנן את המסלול שלו, אבל בסופו של דבר הוא הצליח לעשות זאת. איך הוא הצליח? אל תשכחו שצריך לבקר בכל עיר פעם אחת, ולא יותר מפעם אחת.
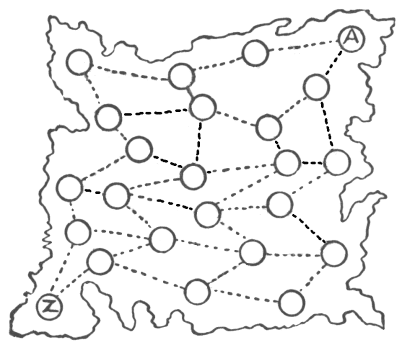 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 250
-
חידת חלת הדבש
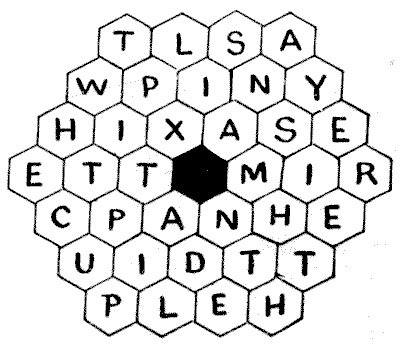 הנה חידה קטנה עם התנאים הפשוטים ביותר האפשריים. הניחו את חוד העיפרון שלכם על אות באחד התאים של חלת הדבש, ועקבו אחר פתגם מוכר מאוד על ידי מעבר תמיד מתא לתא הסמוך לו. אם תבחרו בדרך הנכונה, תבקרו בכל תא פעם אחת בלבד. החידה קלה בהרבה ממה שהיא נראית.
מקורות:נושאים:חידות ורבוסים
הנה חידה קטנה עם התנאים הפשוטים ביותר האפשריים. הניחו את חוד העיפרון שלכם על אות באחד התאים של חלת הדבש, ועקבו אחר פתגם מוכר מאוד על ידי מעבר תמיד מתא לתא הסמוך לו. אם תבחרו בדרך הנכונה, תבקרו בכל תא פעם אחת בלבד. החידה קלה בהרבה ממה שהיא נראית.
מקורות:נושאים:חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 260
-
חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים
אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 262