קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
חידה לשחקני קלפים
שנים עשר חברים במועדון תכננו לשחק ברידג' יחד באחד עשר ערבים, אך אף שחקן לא ישחק עם אותו שותף יותר מפעם אחת, או נגד אותו יריב יותר מפעמיים. האם תוכלו לתכנן תרשים המראה כיצד כולם יכולים לשבת בשלושה שולחנות בכל ערב? קראו לשנים עשר השחקנים על פי שתים עשרה האותיות הראשונות של האלף-בית ונסו לקבץ אותם. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 265
-
טורניר טניס
ארבעה זוגות נשואים שיחקו טורניר טניס "זוגות מעורבים", גבר ואישה תמיד משחקים נגד גבר ואישה. אבל אף אדם לא שיחק עם או נגד אדם אחר יותר מפעם אחת. האם תוכלו להראות כיצד כולם יכלו לשחק יחד בשני מגרשים בשלושה ימים עוקבים? זוהי חידה קטנה מסוג מעשי למדי, והיא מבלבלת במידה מספקת כדי להיות מעניינת. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 266
-
הכובעים הלא נכונים
"אחד הדברים המבלבלים ביותר שנתקלתי בהם לאחרונה," אמר מר ווילסון, "הוא זה. שמונה גברים סעדו בחוכמה פחותה מדי במסעדה לונדונית מסוימת. הם היו האחרונים לעזוב, אך אף גבר לא היה במצב לזהות את הכובע שלו. עכשיו, בהתחשב בכך שהם לקחו את הכובעים שלהם באופן אקראי, מה הסיכויים שכל גבר לקח כובע שלא היה שייך לו?"
"הדבר הראשון," אמר מר ווטרסון, "הוא לראות בכמה דרכים שונות ניתן לקחת את שמונת הכובעים."
"זה די קל," הסביר מר סטאבס. "כפלו יחד את המספרים, `1, 2, 3, 4, 5, 6, 7`, ו-`8`. תן לי לראות—חצי דקה—כן; יש `40,320` דרכים שונות."
"עכשיו כל מה שאתה צריך לעשות זה לראות בכמה מהמקרים האלה לאף אחד אין את הכובע שלו," אמר מר ווטרסון."
תודה, אני לא לוקח כלום," אמר מר פקהרסט. "אני לא מקנא באיש שמנסה לבצע את המשימה של כתיבת כל ארבעים אלף המקרים המוזרים האלה ואז לבחור את אלה שהוא רוצה."
כולם הסכימו שהחיים לא מספיק ארוכים בשביל סוג כזה של שעשוע; ומכיוון שאף אחד לא ראה דרך אחרת להגיע לתשובה, העניין נדחה לזמן בלתי מוגבל. האם אתה יכול לפתור את החידה?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 267
-
צלצול הפעמונים
כתב לי קורספונדנט, שככל הנראה מתעניין מאוד בקמפנולוגיה, ושאל אותי איך עליו לבנות מה שהוא מכנה "צלצול אמיתי ונכון" עבור ארבעה פעמונים. הוא אומר שכל פרמוטציה אפשרית של ארבעת הפעמונים חייבת לצלצל פעם אחת, ופעם אחת בלבד. הוא מוסיף שאף פעמון לא חייב לזוז יותר ממקום אחד בכל פעם, שאף פעמון לא חייב להכות יותר משתי מכות רצופות במקום הראשון או האחרון, ושהשינוי האחרון חייב להיות מסוגל לעבור לראשון. ניתן לראות שתנאים פנטסטיים אלה נשמרים בצליל הקטן לשלושה פעמונים, כדלקמן:—
1 2 3 2 1 3 2 3 1 3 2 1 3 1 2 1 3 2 כיצד עלינו לתת לו פתרון נכון לארבעת הפעמונים שלו?
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 268
-
שלושה אנשים בסירה
יצרן לונדוני נדיב מעניק מדי שנה לעובדיו שבוע חופשה על שפת הים על חשבונו. שנה אחת חמישה-עשר מעובדיו ביקרו בהרן ביי. בבוקר יציאתם מלונדון, פנה אליהם מעסיקם, שביטא את תקוותו שיבלו זמן נעים מאוד.
"הבנתי," הוסיף, "שחלקכם אוהבים מאוד לשוט, ולכן אני מציע הפעם לספק לכם את הבילוי הזה, ובמקביל לתת לכם חידה משעשעת קטנה לפתור. במהלך שבעת הימים שבהם תשהו בהרן ביי, כל אחד מכם ייצא מדי יום בשעה קבועה לשייט, אך תמיד צריכים להיות שלושה אנשים בסירה ולא יותר. אסור לשני אנשים לצאת יחד בסירה יותר מפעם אחת, ואסור לאף אדם לצאת פעמיים באותה סירה. אם תצליחו לעשות זאת, ולהשתמש בכמה שפחות סירות שונות, תוכלו לחייב את החברה בהוצאות."
אחד האנשים מספר לי שהניסיון שרכש בעניינים כאלה איפשר לו במהרה למצוא את הפתרון לשביעות רצונם המלאה ולשביעות רצונו של מעסיקם. אבל החלק המשעשע בעניין הוא שהם מעולם לא פתרו באמת את התעלומה הקטנה. אני מוצא שהשיטה שלהם הייתה שגויה לחלוטין, ואני חושב שזה ישעשע את קוראיי לגלות כיצד היה צריך להציב את האנשים בסירות. מכיוון ששמותיהם הם אנדרוז, בייקר, קרטר, דנבי, אדוארדס, פרית, גיי, הארט, אייזקס, ג'קסון, קנט, לאנג, מייסון, נאפר ואונסלו, נוכל לקרוא להם לפי ראשי התיבות שלהם ולכתוב את חמש הקבוצות לכל אחד משבעת הימים בצורה הפשוטה הבאה:
1 2 3 4 5 יום ראשון: (ABC) (DEF) (GHI) (JKL) (MNO). ניתן לראות כאן שהאנשים בתוך כל זוג סוגריים נמצאים באותה סירה, ולכן A לעולם לא יכול לצאת עם B או עם C שוב, ו-C לעולם לא יכול לצאת שוב עם B. אותו הדבר חל על ארבע הסירות האחרות. המספרים מראים את המספר על הסירה, כך ש-A, B או C, למשל, לעולם לא יכולים לצאת בסירה מס' `1` שוב.
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 269
-
כדורי הזכוכית
מספר קלעים פיקחים שהו שהו באחוזה כפרית, והמארח, כדי לספק קצת בידור, תלה שרשראות של כדורי זכוכית, כפי שמוצג באיור, כדי לירות עליהם. לאחר שכולם העמידו את כישוריהם למבחן מספיק, מישהו שאל את השאלה הבאה: "מהו המספר הכולל של דרכים שונות בהן ניתן לשבור את ששת-עשר הכדורים האלה, אם עלינו תמיד לשבור את הכדור הנמוך ביותר שנותר על כל חוט?" לדוגמה, דרך אחת תהיה לשבור את כל ארבעת הכדורים על כל חוט ברצף, תוך לקיחת החוטים משמאל לימין. דרך נוספת תהיה לשבור תחילה את כל הכדורים הרביעיים על ארבעת החוטים, ואז לשבור את שלושת הנותרים על החוט הראשון, ואז לקחת את הכדורים על שלושת החוטים האחרים לסירוגין מימין לשמאל, וכן הלאה. יש מספר עצום של דרכים שונות (מכיוון שכל וריאציה קטנה של סדר יוצרת דרך שונה) שאדם נוטה להתרשם בתחילה מהקושי הגדול של הבעיה. עם זאת, זה ממש פשוט ברגע שמצאת את השיטה הנכונה לתקוף אותה. כמה דרכים שונות יש?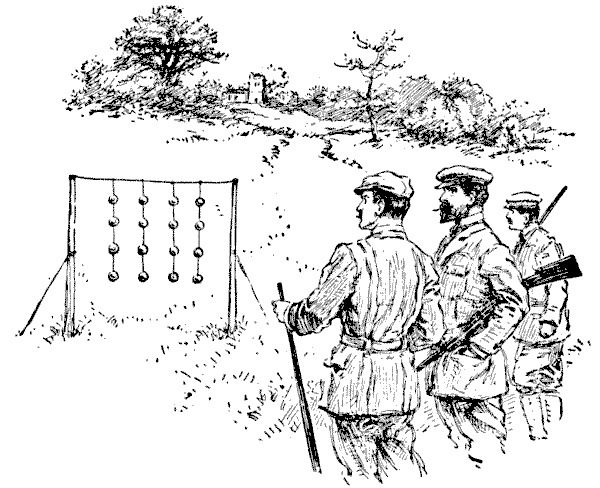 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 270
-
חידה של חמש עשרה אותיות
ALE FOE HOD BGN CAB HEN JOG KFM HAG GEM MOB BFH FAN KIN JEK DFL JAM HIM GCL LJH AID JIB FCJ NJD OAK FIG HCK MLN BED OIL MCD BLK ICE CON DGK הטבלה מעל היא הפתרון לחידה שנתתי ב-Tit-bits בקיץ של `1896`. היה נדרש לקחת את האותיות A, B, C, D, E, F, G, H, I, J, K, L, M, N, ו-O, ויחד איתם ליצור שלושים וחמש קבוצות של שלוש אותיות כך שהצירופים יכללו את המספר הגדול ביותר האפשרי של מילים נפוצות באנגלית. אסור ששתי אותיות יופיעו יחד בקבוצה יותר מפעם אחת. לכן, A ו-L שהיו יחד ב-ALE, לעולם לא ימצאו יחד שוב; וגם אסור ש-A יופיע שוב בקבוצה עם E, או L עם E. תנאים אלה יתקיימו בפתרון לעיל, ומספר המילים שנוצרו הוא עשרים ואחת. אנשים רבים ניסו מאז קשה לנצח את המספר הזה, אבל עד כה לא הצליחו.
לא ניתן ליצור יותר משלושים וחמישה צירופים של חמש עשרה האותיות במסגרת התנאים. מבחינה תיאורטית, לא יכולות להיווצר יותר מעשרים ושלוש מילים, מכיוון שרק מספר זה של צירופים אפשרי עם תנועה או תנועות בכל אחת מהן. ומכיוון שלא ניתן ליצור מילה באנגלית משלוש מהתנועות הנתונות (A, E, I ו-O), עלינו לצמצם את מספר המילים האפשריות לעשרים ושתיים. זה נכון מבחינה תיאורטית, אבל בפועל אי אפשר להשיג את המילה העשרים ושתיים הזו. אם JEK, המוצג לעיל, הייתה מילה, זה היה בסדר גמור; אבל זה לא, ושום כמות של להטוטנות עם שאר האותיות לא הביאה לתוצאה טובה יותר מהמוצגת. עלי לציין ששמות עצם וקיצורים, כמו Joe, Jim, Alf, Hal, Flo, Ike וכו', אינם מותרים.
כעת, החידה הנוכחית היא וריאציה של הנ"ל. זה פשוט: במקום להשתמש בחמש עשרה האותיות הנתונות, הקורא רשאי לבחור כל חמש עשרה אותיות שונות של האלפבית שהוא מעדיף. לאחר מכן בנה שלושים וחמש קבוצות בהתאם לתנאים, והצג כמה שיותר מילים טובות באנגלית.
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 271
-
תשעת תלמידי בית הספר
זוהי חידה נלווית חדשה ומעניינת ל"חמש עשרה תלמידות בית הספר" (ראו פתרון מס' `269`), ואפילו בצורה הפשוטה ביותר שבה אני מציג אותה יש קשיים שאין עליהם עוררין. תשעה תלמידי בית ספר יוצאים בשלשות בששת ימי השבוע כך שאף ילד לא הולך אי פעם זה לצד זה עם ילד אחר יותר מפעם אחת. איך הייתם מסדרים אותם?
אם נציג אותם באמצעות תשע האותיות הראשונות של האלף-בית, הם עשויים להיות מקובצים ביום הראשון כדלקמן:—
A B C D E F G H I אז A לעולם לא יכול ללכת שוב זה לצד זה עם B, או B עם C, או D עם E, וכן הלאה. אבל A יכול, כמובן, ללכת זה לצד זה עם C. זה כאן לא עניין של להיות ביחד באותה שלישייה, אלא של ללכת זה לצד זה בשלישייה. בתנאים אלה הם יכולים לצאת לטיול שישה ימים; בתנאי "תלמידות בית הספר" הם יכולים לטייל רק ארבעה ימים.
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 272
-
השולחן העגול
להושיב את אותם n אנשים סביב שולחן עגול ב-
`((n-1)(n-2))/2`
מקרים כך שלאף אדם לא יהיו אותם שני שכנים פעמיים. זה, כמובן, שווה ערך לאמירה שכל אדם חייב לשבת פעם אחת, ורק פעם אחת, בין כל זוג אפשרי.
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 273
-
פאזל מלכודת העכברים
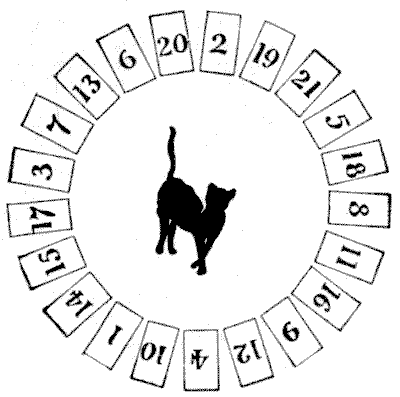 זוהי גרסה מודרנית, עם שינוי, של פאזל ישן בעל אותו השם. מספרו עשרים ואחד כרטיסים, `1, 2, 3` וכו', עד `21`, והניחו אותם במעגל בסדר המסוים המוצג באיור. כרטיסים אלה מייצגים עכברים. אתם מתחילים מכל כרטיס, קוראים לכרטיס הזה "אחד", וסופרים, "אחד, שתיים, שלוש" וכו', בכיוון השעון, וכאשר הספירה שלכם תואמת למספר על הכרטיס, ביצעתם "תפיסה", ואתם מסירים את הכרטיס. לאחר מכן התחילו בכרטיס הבא, קראו לו "אחד", ונסו שוב לבצע "תפיסה" נוספת. וכך הלאה. נניח שאתם מתחילים ב-`18`, וקוראים לכרטיס הזה "אחד", ה"תפיסה" הראשונה שלכם תהיה `19`. הסירו את `19` וה"תפיסה" הבאה שלכם היא `10`. הסירו את `10` וה"תפיסה" הבאה שלכם היא `1`. הסירו את `1`, ואם תספרו עד `21` (אסור לכם לחרוג), לא תוכלו לבצע "תפיסה" נוספת. כעת, האידיאל הוא "לתפוס" את כל עשרים ואחד העכברים, אך זה לא אפשרי כאן, ואם זה היה אפשרי, זה היה דורש רק עשרים ואחד ניסיונות שונים, לכל היותר, כדי להצליח. אבל הקורא רשאי להחליף בין שני כרטיסים לפני שהוא מתחיל. כך, אתם יכולים להחליף את ה-`6` עם ה-`2`, או את ה-`7` עם ה-`11`, או כל זוג אחר. ניתן לעשות זאת בכמה דרכים כדי לאפשר לכם "לתפוס" את כל עשרים ואחד העכברים, אם אז תתחילו במקום הנכון. לעולם אסור לכם לעבור על פני "תפיסה"; אתם תמיד חייבים להסיר את הכרטיס ולהתחיל מחדש.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
זוהי גרסה מודרנית, עם שינוי, של פאזל ישן בעל אותו השם. מספרו עשרים ואחד כרטיסים, `1, 2, 3` וכו', עד `21`, והניחו אותם במעגל בסדר המסוים המוצג באיור. כרטיסים אלה מייצגים עכברים. אתם מתחילים מכל כרטיס, קוראים לכרטיס הזה "אחד", וסופרים, "אחד, שתיים, שלוש" וכו', בכיוון השעון, וכאשר הספירה שלכם תואמת למספר על הכרטיס, ביצעתם "תפיסה", ואתם מסירים את הכרטיס. לאחר מכן התחילו בכרטיס הבא, קראו לו "אחד", ונסו שוב לבצע "תפיסה" נוספת. וכך הלאה. נניח שאתם מתחילים ב-`18`, וקוראים לכרטיס הזה "אחד", ה"תפיסה" הראשונה שלכם תהיה `19`. הסירו את `19` וה"תפיסה" הבאה שלכם היא `10`. הסירו את `10` וה"תפיסה" הבאה שלכם היא `1`. הסירו את `1`, ואם תספרו עד `21` (אסור לכם לחרוג), לא תוכלו לבצע "תפיסה" נוספת. כעת, האידיאל הוא "לתפוס" את כל עשרים ואחד העכברים, אך זה לא אפשרי כאן, ואם זה היה אפשרי, זה היה דורש רק עשרים ואחד ניסיונות שונים, לכל היותר, כדי להצליח. אבל הקורא רשאי להחליף בין שני כרטיסים לפני שהוא מתחיל. כך, אתם יכולים להחליף את ה-`6` עם ה-`2`, או את ה-`7` עם ה-`11`, או כל זוג אחר. ניתן לעשות זאת בכמה דרכים כדי לאפשר לכם "לתפוס" את כל עשרים ואחד העכברים, אם אז תתחילו במקום הנכון. לעולם אסור לכם לעבור על פני "תפיסה"; אתם תמיד חייבים להסיר את הכרטיס ולהתחיל מחדש.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 274