קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
שמונה וילות
באחד מפרבריה החיצוניים של לונדון היה לאיש חלקה מרובעת שעליה החליט לבנות שמונה וילות, כפי שמוצג באיור, עם שטח משחקים משותף באמצע. לאחר שהבתים הושלמו, וכולם או חלקם הושכרו, הוא גילה שמספר הדיירים בשלושת הבתים המרכיבים צד של הריבוע היה בכל מקרה תשעה. הוא לא ציין כיצד הדיירים התפלגו, אבל הראיתי במספרים בצדי הבתים דרך אחת שבה זה יכול היה לקרות. החידה היא לגלות את המספר הכולל של הדרכים שבהן כל הבתים או חלקם יכולים להיות מאוכלסים, כך שיהיו תשעה אנשים בכל צד. כדי שלא יהיו אי הבנות, אסביר שלמרות ש-B הוא מה שאנו מכנים שיקוף של A, אלה ייחשבו כשני הסדרים שונים, בעוד ש-C, אם הוא מסתובב, ייתן ארבעה הסדרים; ואם מסתובבים מול מראה, ארבעה הסדרים אחרים. יש לספור את כל שמונתם. מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 276
-
צלבים של מוֹנִים
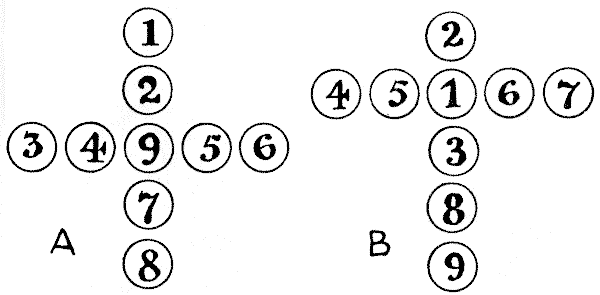
כל מה שאנחנו צריכים לפאזל הזה הם תשעה מוֹנִים, ממוספרים `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. ניתן לראות באיור A שהם מסודרים כך שיוצרים צלב יווני, ואילו במקרה של B הם יוצרים צלב לטיני. בשני המקרים הקורא יגלה שסכום המספרים באנך של הצלב זהה לסכום המספרים בזרוע האופקית. קל למדי להגיע לסידור כזה בניסוי וטעייה, אך הבעיה היא לגלות בדיוק בכמה דרכים שונות ניתן לעשות זאת בכל מקרה. זכרו שהיפוכים ושיקופים אינם נחשבים כשונים. כלומר, אם תסובבו את הדף הזה תקבלו ארבעה סידורים של הצלב היווני, ואם תסובבו אותו שוב מול מראה תקבלו ארבעה נוספים. אבל את שמונתם אלה מחשיבים כזהים. עכשיו, כמה דרכים שונות יש בכל מקרה?
 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 277
-
חביות הבלסם

לסוחר מבגדד היו עשר חביות בלסם יקרות למכירה. הן היו ממוספרות, והיו מסודרות בשתי שורות, אחת על גבי השנייה, כפי שמוצג בתמונה. ככל שהמספר על החבית קטן יותר, כך ערכה גדול יותר. כך שהאיכות הטובה ביותר הייתה ממוספרת ב-"`1`" והגרועה ביותר ממוספרת ב-"`10`", וכל שאר המספרים מייצגים ערכים מדורגים. כעת, הכלל של אחמד אסן, הסוחר, היה שהוא לעולם לא הניח חבית מתחת או מימין לחבית בעלת ערך נמוך יותר. הסידור המוצג הוא, כמובן, הדרך הפשוטה ביותר לקיים תנאי זה. אבל ישנן דרכים רבות אחרות—כגון, לדוגמה, זו:—
1 2 5 7 8 3 4 6 9 10 גם כאן, לאף חבית אין מספר קטן ממנה מימין או מתחתיה. החידה היא לגלות בכמה דרכים שונות יכול היה הסוחר מבגדד לסדר את חביותיו בשתי השורות מבלי להפר את הכלל שלו. האם תוכלו לספור את מספר הדרכים?
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 279
-
בניית הטטרהדרון
יש לי טטרהדרון, או פירמידה משולשת, העשויה משישה מקלות המודבקים זה לזה, כפי שמוצג באיור. האם תוכלו לספור נכונה את מספר הדרכים השונות שבהן ניתן היה להדביק את ששת המקלות הללו יחד כדי ליצור את הפירמידה?
כמה חברים עבדו על זה יחד בערב אחד, כאשר כל אדם מצטייד בשישה גפרורים כדי לעזור למחשבותיו; אבל התברר שאף שתי תוצאות לא היו זהות. אתם רואים, אם נסיר אחד מהמקלות ונסובב אותו לצד השני, זו תהיה פירמידה שונה. אם נחליף בין שניים מהמקלות התוצאה שוב תהיה שונה. אבל זכרו שניתן להעמיד כל פירמידה על כל אחד מארבעת צדדיה מבלי להיות פירמידה שונה. כמה דרכים יש בסך הכל?
מקורות: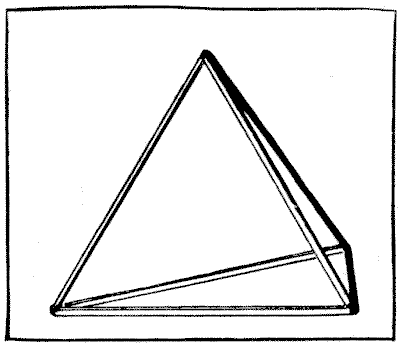
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 280
-
צביעת פירמידה
חידה זו עוסקת בצביעת ארבעת צדדיו של טטרהדרון, או פירמידה משולשת. אם תגזרו חתיכת קרטון בצורה משולשת כפי שמוצג באיור `1`, ואז תחצו אותה לאורך הקווים המקווקווים, היא תתקפל ותצור פירמידה משולשת מושלמת. ברצוני להזכיר לקוראיי שצבעי היסוד של הספקטרום הסולארי הם שבעה - סגול, אינדיגו, כחול, ירוק, צהוב, כתום ואדום. כשהייתי ילד לימדו אותי לזכור אותם באמצעות המילה המגושמת שנוצרה על ידי ראשי התיבות של הצבעים, "Vibgyor".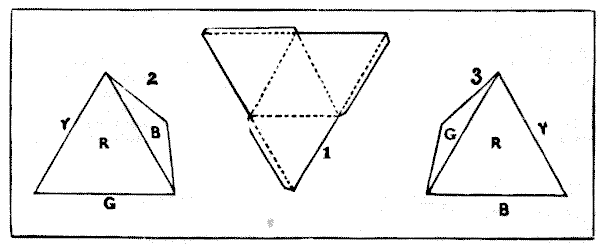 בכמה דרכים שונות ניתן לצבוע את הפירמידה המשולשת, תוך שימוש בכל מקרה בצבע אחד, שניים, שלושה או ארבעה מצבעי הספקטרום הסולארי? כמובן שצד יכול לקבל רק צבע בודד, ואף צד לא יכול להישאר לא צבוע. אבל יש נקודה אחת שאני חייב להבהיר. אין לראות בארבעת הצדדים כנפרדים מבחינה אינדיבידואלית. כלומר, אם תצבעו את הפירמידה שלכם כפי שמוצג באיור `2` (כאשר הצד התחתון ירוק והצד השני שאינו נראה הוא צהוב), ואז תצבעו אחרת בסדר המוצג באיור `3`, אלה באמת אותו הדבר ונספרים כדרך אחת. כי אם תטו את מס' `2` ימינה, הוא ייפול כך שייצג את מס' `3`. הימנעות מחזרות מסוג זה היא החידה האמיתית של העניין. אם לא ניתן למקם פירמידה צבעונית כך שתדמה בדיוק בצבעיה ובסדר היחסי שלהם לפירמידה אחרת, אז הן שונות. זכרו שדרך אחת תהיה לצבוע את כל ארבעת הצדדים באדום, אחרת לצבוע שני צדדים בירוק, ואת הצדדים הנותרים בצהוב וכחול; וכן הלאה.
מקורות:
בכמה דרכים שונות ניתן לצבוע את הפירמידה המשולשת, תוך שימוש בכל מקרה בצבע אחד, שניים, שלושה או ארבעה מצבעי הספקטרום הסולארי? כמובן שצד יכול לקבל רק צבע בודד, ואף צד לא יכול להישאר לא צבוע. אבל יש נקודה אחת שאני חייב להבהיר. אין לראות בארבעת הצדדים כנפרדים מבחינה אינדיבידואלית. כלומר, אם תצבעו את הפירמידה שלכם כפי שמוצג באיור `2` (כאשר הצד התחתון ירוק והצד השני שאינו נראה הוא צהוב), ואז תצבעו אחרת בסדר המוצג באיור `3`, אלה באמת אותו הדבר ונספרים כדרך אחת. כי אם תטו את מס' `2` ימינה, הוא ייפול כך שייצג את מס' `3`. הימנעות מחזרות מסוג זה היא החידה האמיתית של העניין. אם לא ניתן למקם פירמידה צבעונית כך שתדמה בדיוק בצבעיה ובסדר היחסי שלהם לפירמידה אחרת, אז הן שונות. זכרו שדרך אחת תהיה לצבוע את כל ארבעת הצדדים באדום, אחרת לצבוע שני צדדים בירוק, ואת הצדדים הנותרים בצהוב וכחול; וכן הלאה.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 281
-
השרשרת של חוקר העתיקות
לחוקר עתיקות הייתה כמות של חוליות עתיקות מוזרות, אותן לקח לנפח, וביקש ממנו לחבר אותן יחד ליצירת שרשרת ישרה אחת, בתנאי היחיד ששתי החוליות העגולות לא יהיו יחד. האיור הבא מציג את מראה השרשרת ואת צורתה של כל חוליה. כעת, נניח שהבעלים יפריד שוב את החוליות, ואז ייקח אותן לנפח אחר ויחזור בדיוק על ההוראות הקודמות שלו, מה הסיכויים שהחוליות לא יורכבו בדיוק כפי שהורכבו על ידי הנפח הראשון? זכרו שכל חוליה עוקבת יכולה להיות מחוברת לאחרת באחת משתי דרכים, בדיוק כפי שאתם יכולים לשים טבעת על האצבע שלכם בשתי דרכים, או לחבר את האצבעות המורות והאגודלים שלכם בשתי דרכים.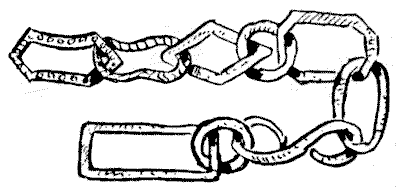 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 282
-
חֲמֵשׁ עֶשְׂרֵה אֲבָנֵי דּוֹמִינוֹ
במקרה זה, איננו משתמשים בערכה השלמה של עשרים ושמונה אבני דומינו המצויות בקופסה רגילה. אנו מוותרים על כל אבני הדומינו שיש עליהן חמש או שש ומגבילים את עצמנו לחמש-עשרה הנותרות, כאשר ארבע-כפול-ארבע היא הגבוהה ביותר.
בכמה דרכים שונות ניתן לסדר את חמש-עשרה אבני הדומינו בקו ישר בהתאם לכלל הפשוט של המשחק, שלפיו יש להניח תמיד מספר מול מספר דומה – כלומר, ארבע מול ארבע, ריק מול ריק, וכן הלאה? משמאל לימין ומימין לשמאל של אותו סידור ייחשבו כשתי דרכים שונות.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 283
-
מטרת הצלב
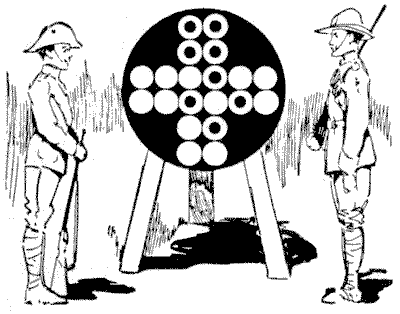 באיור יש לנו מטרה מעט מוזרה שעוצבה על ידי צלף אקסצנטרי. הרעיון שלו היה שכדי לצבור ניקוד, עליך לפגוע בארבעה עיגולים בארבע יריות כך שאותן ארבע יריות ייצרו ריבוע. ניתן לראות מהתוצאות שנרשמו על המטרה ששני ניסיונות הצליחו. האדם הראשון פגע בארבעת העיגולים בראש הצלב, ובכך יצר את הריבוע שלו. האדם השני התכוון לפגוע בארבעת העיגולים בזרוע התחתונה, אך היריה השנייה שלו, בצד שמאל, הייתה גבוהה מדי. זה אילץ אותו להשלים את הארבעה שלו בצורה שונה ממה שהוא התכוון. כך ניתן לראות שלמרות שזה לא משנה באיזה עיגול אתה פוגע ביריה הראשונה, היריה השנייה עשויה לחייב אותך לנוהל מוגדר אם אתה רוצה להשיג את הריבוע שלך. כעת, החידה היא לומר בכמה דרכים שונות אפשר ליצור ריבוע על המטרה עם ארבע יריות.
מקורות:נושאים:גאומטריה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
באיור יש לנו מטרה מעט מוזרה שעוצבה על ידי צלף אקסצנטרי. הרעיון שלו היה שכדי לצבור ניקוד, עליך לפגוע בארבעה עיגולים בארבע יריות כך שאותן ארבע יריות ייצרו ריבוע. ניתן לראות מהתוצאות שנרשמו על המטרה ששני ניסיונות הצליחו. האדם הראשון פגע בארבעת העיגולים בראש הצלב, ובכך יצר את הריבוע שלו. האדם השני התכוון לפגוע בארבעת העיגולים בזרוע התחתונה, אך היריה השנייה שלו, בצד שמאל, הייתה גבוהה מדי. זה אילץ אותו להשלים את הארבעה שלו בצורה שונה ממה שהוא התכוון. כך ניתן לראות שלמרות שזה לא משנה באיזה עיגול אתה פוגע ביריה הראשונה, היריה השנייה עשויה לחייב אותך לנוהל מוגדר אם אתה רוצה להשיג את הריבוע שלך. כעת, החידה היא לומר בכמה דרכים שונות אפשר ליצור ריבוע על המטרה עם ארבע יריות.
מקורות:נושאים:גאומטריה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 284
-
ארבעה בולי דואר
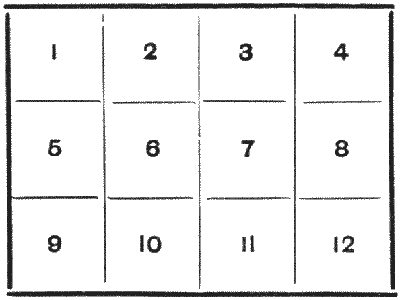 "זה קל כמו לספור", הוא ביטוי שאדם שומע לעתים. אבל ספירה פשוטה עשויה להיות מבלבלת לעתים. קחו את הדוגמה הפשוטה הבאה. נניח שזה עתה קניתם שנים-עשר בולי דואר, בצורה הזו - שלושה על ארבעה - וחבר מבקש מכם להואיל בטובכם לתת לו ארבעה בולים, כולם מחוברים יחד - בלי שאף בול יהיה תלוי רק בפינה. בכמה דרכים שונות אפשר לתלוש את ארבעת הבולים האלה? אתם רואים, אתם יכולים לתת לו `1, 2, 3, 4`, או `2, 3, 6, 7`, או `1, 2, 3, 6`, או `1, 2, 3, 7`, או `2, 3, 4, 8`, וכן הלאה. האם תוכלו לספור את מספר הדרכים השונות בהן ניתן למסור את ארבעת הבולים האלה? אין הרבה יותר מחמישים דרכים, אז זה לא ספירה גדולה. האם תוכלו לקבל את המספר המדויק?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
"זה קל כמו לספור", הוא ביטוי שאדם שומע לעתים. אבל ספירה פשוטה עשויה להיות מבלבלת לעתים. קחו את הדוגמה הפשוטה הבאה. נניח שזה עתה קניתם שנים-עשר בולי דואר, בצורה הזו - שלושה על ארבעה - וחבר מבקש מכם להואיל בטובכם לתת לו ארבעה בולים, כולם מחוברים יחד - בלי שאף בול יהיה תלוי רק בפינה. בכמה דרכים שונות אפשר לתלוש את ארבעת הבולים האלה? אתם רואים, אתם יכולים לתת לו `1, 2, 3, 4`, או `2, 3, 6, 7`, או `1, 2, 3, 6`, או `1, 2, 3, 7`, או `2, 3, 4, 8`, וכן הלאה. האם תוכלו לספור את מספר הדרכים השונות בהן ניתן למסור את ארבעת הבולים האלה? אין הרבה יותר מחמישים דרכים, אז זה לא ספירה גדולה. האם תוכלו לקבל את המספר המדויק?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 285
-
צביעת הקובייה
בכמה דרכים שונות ניתן לסמן את המספרים על קובייה בודדת, כאשר התנאי היחיד הוא שהמספרים `1` ו-`6`, המספרים `2` ו-`5`, והמספרים `3` ו-`4` חייבים להיות על צדדים נגדיים? זו שאלה פשוטה למדי, ובכל זאת היא תבלבל אנשים רבים.מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 286