קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
פאזל אקרוסטיכון
בהכנה או בפתרון של אקרוסטיכונים כפולים, האם עלה בדעתכם לשקול את המגוון והמגבלה של צמד האותיות הראשוניות והסופיות הזמינות למילים מצטלבות? ייתכן שתצטרכו למצוא מילה שמתחילה ב-A ומסתיימת ב-B, או A ו-C, או A ו-D, וכן הלאה. שילובים מסוימים הם בלתי אפשריים בעליל—כגון, למשל, אלה עם Q בסוף. אבל נניח שאפשר למצוא מילה אנגלית טובה לכל מקרה. אז כמה צמדי אותיות אפשריים זמינים?
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 287
-
חלוקות לוח שחמט
לאחרונה שאלתי את עצמי את השאלה: בכמה דרכים שונות ניתן לחלק לוח שחמט לשני חלקים באותו גודל וצורה על ידי חתכים לאורך הקווים המחלקים את הריבועים? עד מהרה התברר שהבעיה מרתקת ומלאת קשיים. אני מציג אותה בצורה פשוטה, תוך שימוש בלוח בעל ממדים קטנים יותר. ברור שלוח של ארבעה ריבועים יכול להיות מחולק רק בדרך אחת - על ידי חיתוך ישר במרכז - מכיוון שלא נספור היפוכים ושיקופים כשונים. במקרה של לוח של שישה עשר ריבועים - ארבעה על ארבעה - יש בדיוק שש דרכים שונות. נתתי את כולן בתרשים, והקורא לא ימצא אחרות. כעת, קחו את הלוח הגדול יותר של שלושים ושישה ריבועים, ונסו לגלות בכמה דרכים ניתן לחתוך אותו לשני חלקים באותו גודל וצורה.
מקורות:
ברור שלוח של ארבעה ריבועים יכול להיות מחולק רק בדרך אחת - על ידי חיתוך ישר במרכז - מכיוון שלא נספור היפוכים ושיקופים כשונים. במקרה של לוח של שישה עשר ריבועים - ארבעה על ארבעה - יש בדיוק שש דרכים שונות. נתתי את כולן בתרשים, והקורא לא ימצא אחרות. כעת, קחו את הלוח הגדול יותר של שלושים ושישה ריבועים, ונסו לגלות בכמה דרכים ניתן לחתוך אותו לשני חלקים באותו גודל וצורה.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 288
-
אריות וכתרים
הגברת הצעירה באיור מתמודדת עם קושי קטן בגזירה, שבו הקורא ישמח לסייע לה. היא רוצה, מסיבה כלשהי שהיא לא מסרה לי, לחתוך את חתיכת הבד המרובעת והיקרה הזו לארבעה חלקים, כולם בדיוק באותו גודל ובאותה צורה, אבל חשוב שכל חתיכה תכיל אריה וכתר. מכיוון שהיא מתעקשת שהחתכים ייעשו רק לאורך הקווים המחלקים את הריבועים, היא נבוכה למדי לגלות איך לעשות זאת. האם תוכלו להראות לה את הדרך? יש רק שיטה אפשרית אחת לחתוך את הבד.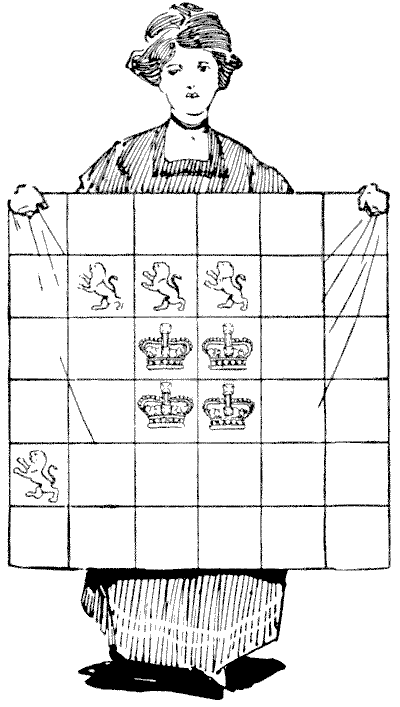 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 289
-
לוחות עם מספר אי-זוגי של משבצות
אנו נדון כאן בשאלה של אותם לוחות המכילים מספר אי-זוגי של משבצות. נניח שהמשבצת המרכזית נחתכת תחילה, כך שיישאר מספר זוגי של משבצות לחלוקה. כעת, ברור שלוח ריבוע שלוש על שלוש ניתן לחלוקה רק בדרך אחת, כפי שמוצג באיור `1`. ניתן לראות שהחלקים A ו-B הם באותו גודל וצורה, וכי כל דרך חיתוך אחרת תייצר רק חלקים בעלי צורה זהה, אז זכרו שווריאציות אלה אינן נספרות כדרכים שונות. החידה שאני מציע היא לחתוך את הלוח חמש על חמש (איור `2`) לשני חלקים באותו גודל וצורה בכמה שיותר דרכים שונות. הדגמתי באיור דרך אחת לעשות זאת. כמה דרכים שונות יש בסך הכל? חתיכה שכאשר הופכים אותה דומה לחתיכה אחרת אינה נחשבת כבעלת צורה שונה.
 מקורות:נושאים:גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
מקורות:נושאים:גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 290
-
הבעיה של הגראנד לאמה
לפני זמן רב היה גראנד לאמה שהייתה לו לוח שחמט עשוי זהב טהור, חרוט בצורה מפוארת, וכמובן, בעל ערך רב. מדי שנה נערך טורניר בלהסה בין הכמרים, ובכל פעם שמישהו ניצח את הגראנד לאמה זה נחשב לכבוד גדול, ושמו נכתב על גב הלוח, ותכשיט יקר הוצב במשבצת המסוימת שבה ניתן השחמט. לאחר שהפונטיף הריבוני הזה הובס בארבעה מקרים הוא מת - אולי מצער.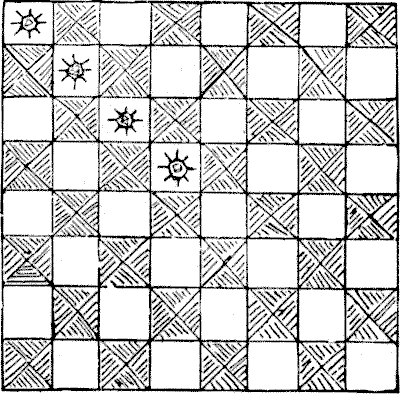 כעת הגראנד לאמה החדש היה שחקן שחמט נחות, והעדיף צורות אחרות של שעשוע תמים, כמו עריפת ראשים של אנשים. אז הוא פסל את השחמט כמשחק משפיל, שלא שיפר לא את המוח ולא את המוסר, וביטל את הטורניר באופן מיידי. ואז הוא שלח לארבעת הכמרים שהייתה להם החוצפה לשחק טוב יותר מגראנד לאמה, ופנה אליהם כדלקמן: "אנשים עלובים וכופרים, המכנים את עצמכם כמרים! האם אינכם יודעים שלטעון ליכולת לעשות משהו טוב יותר מקודמי הוא עבירה שעונשה מוות? קחו את לוח השחמט הזה ולפני שהשחר יעלה על חדר העינויים, חתכו אותו לארבעה חלקים שווים בעלי אותו צורה, שכל אחד מהם מכיל שישה עשר ריבועים מושלמים, עם אחד מהאבנים היקרות בכל חלק! אם תיכשלו בכך, אז יומצאו ספורט אחרים להנאתכם המיוחדת. לכו!" ארבעת הכמרים הצליחו במשימתם שנראתה חסרת סיכוי. האם תוכלו להראות כיצד ניתן לחלק את הלוח לארבעה חלקים שווים, שכל אחד מהם בעל אותו צורה בדיוק, על ידי חיתוכים לאורך הקווים המחלקים את הריבועים, כאשר כל חלק מכיל אחת מהאבנים היקרות?
מקורות:נושאים:קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים
כעת הגראנד לאמה החדש היה שחקן שחמט נחות, והעדיף צורות אחרות של שעשוע תמים, כמו עריפת ראשים של אנשים. אז הוא פסל את השחמט כמשחק משפיל, שלא שיפר לא את המוח ולא את המוסר, וביטל את הטורניר באופן מיידי. ואז הוא שלח לארבעת הכמרים שהייתה להם החוצפה לשחק טוב יותר מגראנד לאמה, ופנה אליהם כדלקמן: "אנשים עלובים וכופרים, המכנים את עצמכם כמרים! האם אינכם יודעים שלטעון ליכולת לעשות משהו טוב יותר מקודמי הוא עבירה שעונשה מוות? קחו את לוח השחמט הזה ולפני שהשחר יעלה על חדר העינויים, חתכו אותו לארבעה חלקים שווים בעלי אותו צורה, שכל אחד מהם מכיל שישה עשר ריבועים מושלמים, עם אחד מהאבנים היקרות בכל חלק! אם תיכשלו בכך, אז יומצאו ספורט אחרים להנאתכם המיוחדת. לכו!" ארבעת הכמרים הצליחו במשימתם שנראתה חסרת סיכוי. האם תוכלו להראות כיצד ניתן לחלק את הלוח לארבעה חלקים שווים, שכל אחד מהם בעל אותו צורה בדיוק, על ידי חיתוכים לאורך הקווים המחלקים את הריבועים, כאשר כל חלק מכיל אחת מהאבנים היקרות?
מקורות:נושאים:קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 291
-
החלון של האב המנזר
לפני שנים רבות, האב המנזר מסנט אדמונדסברי, כתוצאה מ"מסירות חזקה מדי לראשו," חלה ולא היה מסוגל לעזוב את מיטתו. כששכב ער, מטלטל את ראשו באי שקט מצד לצד, הנזירים הקשובים הבחינו שמשהו מטריד את מחשבותיו; אך איש לא העז לשאול מה זה יכול להיות, כי האב המנזר היה בעל אופי קשוח, ומעולם לא סבל סקרנות. לפתע קרא לאב ג'ון, והנזיר המכובד ההוא מיהר למיטתו.
"אב ג'ון," אמר האב המנזר, "האם אתה יודע שנולדתי לעולם הנורא הזה בערב חג המולד?
"הנזיר הנהן בהסכמה.
"והאם לא אמרתי לך לעתים קרובות, שנולדתי בערב חג המולד, שאין לי אהבה לדברים שהם אי-זוגיים? תסתכל שם!"
האב המנזר הצביע על חלון המעונות הגדול, שממנו אני נותן סקיצה. הנזיר הביט, והיה נבוך.
"האם אינך רואה ששישים וארבעת האורות מסתכמים למספר זוגי אנכית ואופקית, אך כל הקווים האלכסוניים, למעט ארבעה עשר, הם מספר שהוא אי-זוגי? מדוע זה?"
"אכן, אדוני האב המנזר, זה טבע הדברים, ואי אפשר לשנות זאת."
"לא, אבל זה יש ישתנה. אני מצווה עליך שחלק מהאורות ייחסמו היום, כך שלכל קו יהיה מספר זוגי של אורות. ראה שזה נעשה ללא דיחוי, שמא המרתפים יינעלו לחודש וצרות קשות אחרות יפקדו אותך."
אב ג'ון היה חסר אונים, אך לאחר התייעצות עם מישהו שהיה בקיא בתעלומות מוזרות, נמצאה דרך לספק את גחמתו של האב המנזר. אילו אורות נחסמו, כך שאלה שנותרו הסתכמו למספר זוגי בכל קו אופקית, אנכית ואלכסונית, תוך גרימת ההפרעה המינימלית האפשרית לאור?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 292
-
לוח השחמט הסיני
לאיזה מספר גדול של חלקים שונים ניתן לחתוך את לוח השחמט (על ידי חיתוכים לאורך הקווים בלבד), כך שלא יהיו שני חלקים זהים לחלוטין? זכרו שסידור השחור והלבן מהווה הבדל. כך, ריבוע שחור בודד יהיה שונה מריבוע לבן בודד, שורה של שלושה המכילה שני ריבועים לבנים תהיה שונה משורה של שלושה המכילה שני ריבועים שחורים, וכן הלאה. אם לא ניתן להניח שני חלקים על השולחן כך שיהיו זהים לחלוטין, הם נחשבים לשונים. ומכיוון שגב הלוח חלק, לא ניתן להפוך את החלקים.מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 293
-
משפט לוח השחמט

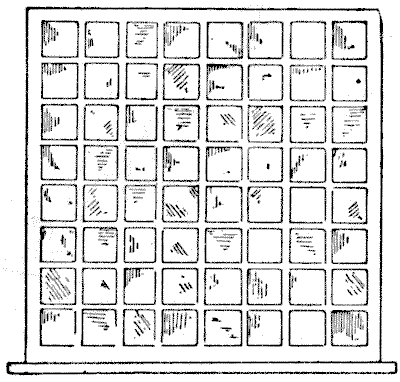
פעם שמתי לעצמי כמשימה משעשעת לנתח לוח שחמט רגיל לאותיות האלף-בית, כך שהן ייצרו משפט שלם. ניתן לראות מהאיור שהחלקים המורכבים יוצרים את המשפט "CUT THY LIFE," עם עצירות בין המילים. המשפט האידיאלי, כמובן, היה בעל עצירה אחת בלבד, אבל לא הצלחתי להשיג זאת.
המשפט הוא קריאה לעבריין להתנתק מחיי הרשע שהוא חי. האם תוכלו לחבר את החלקים האלה כדי ליצור לוח שחמט מושלם?
מקורות:נושאים:קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 294
-
שמונת הצריחים
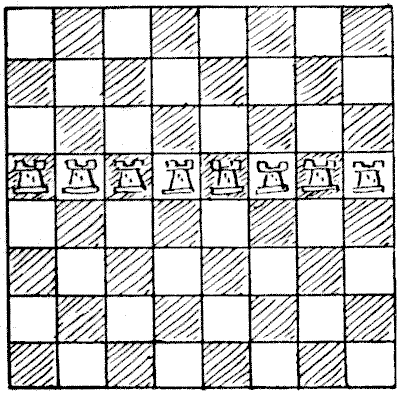 ניתן לראות בדיאגרמה הראשונה שכל משבצת על הלוח מאוכלסת או מותקפת על ידי צריח, וכל צריח "שמור" (אם היו צריחים שחורים ולבנים לסירוגין היינו אומרים "מותקף") על ידי צריח אחר. הצבת שמונת הצריחים על כל שורה או טור תהיה בעלת השפעה זהה. בדיאגרמה `2` כל משבצת שוב מאוכלסת או מותקפת, אך במקרה זה כל צריח אינו שמור. כעת, בכמה דרכים שונות ניתן להציב את שמונת הצריחים על הלוח כך שכל משבצת תהיה מאוכלסת או מותקפת ואף צריח לא יהיה שמור על ידי אחר? אינני רוצה להיכנס לשאלת ההיפוכים והשיקופים בהזדמנות זו, כך שהצבת הצריחים על האלכסון השני תיחשב שונה, וכך גם לגבי חזרות אחרות המתקבלות על ידי סיבוב הלוח.
ניתן לראות בדיאגרמה הראשונה שכל משבצת על הלוח מאוכלסת או מותקפת על ידי צריח, וכל צריח "שמור" (אם היו צריחים שחורים ולבנים לסירוגין היינו אומרים "מותקף") על ידי צריח אחר. הצבת שמונת הצריחים על כל שורה או טור תהיה בעלת השפעה זהה. בדיאגרמה `2` כל משבצת שוב מאוכלסת או מותקפת, אך במקרה זה כל צריח אינו שמור. כעת, בכמה דרכים שונות ניתן להציב את שמונת הצריחים על הלוח כך שכל משבצת תהיה מאוכלסת או מותקפת ואף צריח לא יהיה שמור על ידי אחר? אינני רוצה להיכנס לשאלת ההיפוכים והשיקופים בהזדמנות זו, כך שהצבת הצריחים על האלכסון השני תיחשב שונה, וכך גם לגבי חזרות אחרות המתקבלות על ידי סיבוב הלוח. 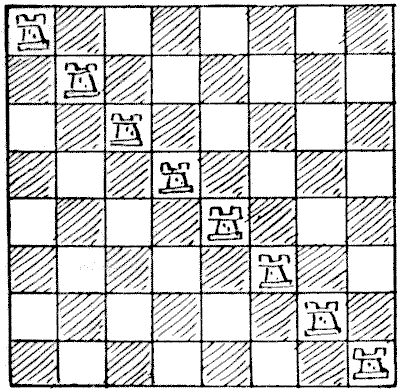 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 295
-
ארבעת האריות
החידה היא למצוא בכמה דרכים שונות ניתן להציב את ארבעת האריות כך שלעולם לא יהיה יותר מאריה אחד בכל שורה או עמודה. היפוכים ושיקופים בלבד לא ייחשבו כשונים. לכן, לגבי הדוגמה הנתונה, אם נציב את האריות באלכסון השני, זה ייחשב לאותו סידור. כי אם תחזיקו את הסידור השני מול מראה או תסובבו אותו ברבע סיבוב, תקבלו רק את הסידור הראשון. זוהי חידה קטנה ופשוטה, אך היא דורשת מידה מסוימת של שיקול דעת זהיר. מקורות:נושאים:קומבינטוריקה
מקורות:נושאים:קומבינטוריקה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 296