קומבינטוריקה, גאומטריה קומבינטורית

גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.

• חתכו סירה לשניים

  צורות גיאומטריות נקראות חופפות אם הן מתלכדות כאשר שמים אותן זו על זו. חתכו את הצורה לשני חלקים חופפים

  

  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ה-ו שאלה 6

• שאלה

  חלקו את הצורה שבציור ל-7 חלקים חופפים.
  

  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • אולימפיאדת בנו ארבל, 2019, כיתה ח שאלה 3

• שאלה

  חלק את הצורה שבציור לשלושה חלקים שווים בשטחם ובצורתם.
  

  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 4

• עבודת טלאים ממשי

  חברות המשפחה ממשפחת וילקינסון הכינו שמיכת טלאים פשוטה, כמתנה קטנה לחג המולד, המורכבת כולה מחתיכות מרובעות באותו גודל, כפי שמוצג באיור. היו חסרות רק ארבע פינות כדי להשלים אותה. מישהו הצביע בפניהן שאם יפרקו את צלב יווני באמצע ואז יחתכו את התפרים לאורך החיבורים הכהים, ארבעת החלקים כולם באותו גודל וצורה יתאימו יחד וייצרו ריבוע. הקורא יודע, מהפתרון באיור `39`, שזה נעשה די בקלות. אבל ג'ורג' וילקינסון הציע להן לפתע את החידה הזו. הוא אמר, "במקום לבחור את הצלב כולו, וליצור את הריבוע מארבעה חלקים שווים, האם תוכלו לחתוך ריבוע שלם וארבעה חלקים שווים שייצרו צלב יווני מושלם?" הפאזל הוא, כמובן, עכשיו די קל.
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 142

• שְׁנֵי צְלָבִים מֵאֶחָד

  חתוך צלב יווני לחמישה חלקים שייצרו שני צלבים כאלה, שניהם באותו גודל. הפתרון של החידה הזו יפה מאוד.
  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 143

• הצלב והמשולש

  חתוך צלב יווני לשישה חלקים שייצרו משולש שווה צלעות. זוהי בעיה קשה נוספת, ואציין כאן שפתרון מעשי בלתי אפשרי ללא ידע מוקדם בשיטה שלי להמרת משולש שווה צלעות לריבוע (ראה מס' `26`, "חידות קנטרברי").
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 144

• הצלב המקופל

  גזרו מצלב יווני מנייר; לאחר מכן קפלו אותו כך שבעזרת חיתוך ישר בודד במספריים, ארבעת החלקים שנוצרו ייצרו ריבוע.

  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 145

• חידת חיתוך קלה

   

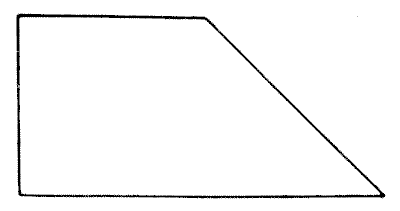
  ראשית, גזרו פיסת נייר או קרטון בצורה המוצגת באיור. ניתן לראות מיד שהפרופורציות הן פשוט אלו של ריבוע המחובר למחצית ריבוע דומה אחר, המחולק באלכסון. החידה היא לחתוך אותו לארבעה חלקים, כולם באותו גודל וצורה בדיוק.

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 146

• חידת ריבוע קלה

   

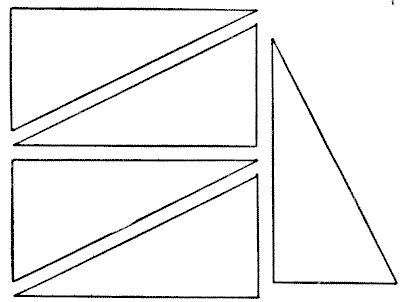
  אם תיקח פיסת קרטון מלבנית, שאורכה כפול מרוחבה, ותחתוך אותה לשניים באלכסון, תקבל שניים מהחלקים המוצגים באיור. החידה היא ליצור ריבוע מחמישה חלקים כאלה בגודל שווה. ניתן לחתוך אחד מהחלקים לשניים, אך יש להשתמש בשאר החלקים בשלמותם.

  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 147

• חידת הלחמנייה

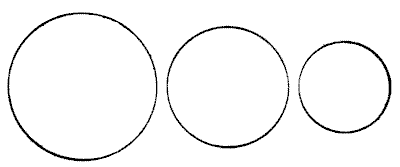  שלושת העיגולים מייצגים שלוש לחמניות, ונדרש פשוט להראות כיצד ניתן לחלק אותן באופן שווה בין ארבעה בנים. יש להתייחס ללחמניות כבעלות עובי שווה לכל אורכן ועובי שווה זו לזו. כמובן, יש לחתוך אותן למספר החלקים המועט ביותר האפשרי. כדי לפשט זאת, אציין את העובדה המפתיעה למדי שדי בחמישה חלקים בלבד, ומכך ניתן יהיה לראות שנער אחד מקבל את חלקו בשני חלקים ושלושת האחרים מקבלים את חלקם בחלק אחד. אני מודע לכך שהצהרה זו "מסגירה" את החידה, אך היא לא אמורה לפגוע בעניינם של אלה שאוהבים לגלות את "הסיבה לכך".
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 148