קומבינטוריקה, גאומטריה קומבינטורית

גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.

• חלוקות לוח שחמט

  לאחרונה שאלתי את עצמי את השאלה: בכמה דרכים שונות ניתן לחלק לוח שחמט לשני חלקים באותו גודל וצורה על ידי חתכים לאורך הקווים המחלקים את הריבועים? עד מהרה התברר שהבעיה מרתקת ומלאת קשיים. אני מציג אותה בצורה פשוטה, תוך שימוש בלוח בעל ממדים קטנים יותר. ברור שלוח של ארבעה ריבועים יכול להיות מחולק רק בדרך אחת - על ידי חיתוך ישר במרכז - מכיוון שלא נספור היפוכים ושיקופים כשונים. במקרה של לוח של שישה עשר ריבועים - ארבעה על ארבעה - יש בדיוק שש דרכים שונות. נתתי את כולן בתרשים, והקורא לא ימצא אחרות. כעת, קחו את הלוח הגדול יותר של שלושים ושישה ריבועים, ונסו לגלות בכמה דרכים ניתן לחתוך אותו לשני חלקים באותו גודל וצורה.
  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 288

• אריות וכתרים

  הגברת הצעירה באיור מתמודדת עם קושי קטן בגזירה, שבו הקורא ישמח לסייע לה. היא רוצה, מסיבה כלשהי שהיא לא מסרה לי, לחתוך את חתיכת הבד המרובעת והיקרה הזו לארבעה חלקים, כולם בדיוק באותו גודל ובאותה צורה, אבל חשוב שכל חתיכה תכיל אריה וכתר. מכיוון שהיא מתעקשת שהחתכים ייעשו רק לאורך הקווים המחלקים את הריבועים, היא נבוכה למדי לגלות איך לעשות זאת. האם תוכלו להראות לה את הדרך? יש רק שיטה אפשרית אחת לחתוך את הבד.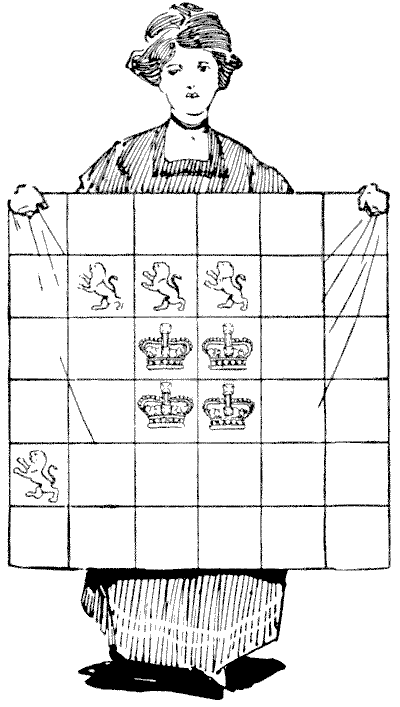
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 289

• לוחות עם מספר אי-זוגי של משבצות

  אנו נדון כאן בשאלה של אותם לוחות המכילים מספר אי-זוגי של משבצות. נניח שהמשבצת המרכזית נחתכת תחילה, כך שיישאר מספר זוגי של משבצות לחלוקה. כעת, ברור שלוח ריבוע שלוש על שלוש ניתן לחלוקה רק בדרך אחת, כפי שמוצג באיור `1`. ניתן לראות שהחלקים A ו-B הם באותו גודל וצורה, וכי כל דרך חיתוך אחרת תייצר רק חלקים בעלי צורה זהה, אז זכרו שווריאציות אלה אינן נספרות כדרכים שונות. החידה שאני מציע היא לחתוך את הלוח חמש על חמש (איור `2`) לשני חלקים באותו גודל וצורה בכמה שיותר דרכים שונות. הדגמתי באיור דרך אחת לעשות זאת. כמה דרכים שונות יש בסך הכל? חתיכה שכאשר הופכים אותה דומה לחתיכה אחרת אינה נחשבת כבעלת צורה שונה.
  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 290

• הבעיה של הגראנד לאמה

  לפני זמן רב היה גראנד לאמה שהייתה לו לוח שחמט עשוי זהב טהור, חרוט בצורה מפוארת, וכמובן, בעל ערך רב. מדי שנה נערך טורניר בלהסה בין הכמרים, ובכל פעם שמישהו ניצח את הגראנד לאמה זה נחשב לכבוד גדול, ושמו נכתב על גב הלוח, ותכשיט יקר הוצב במשבצת המסוימת שבה ניתן השחמט. לאחר שהפונטיף הריבוני הזה הובס בארבעה מקרים הוא מת - אולי מצער.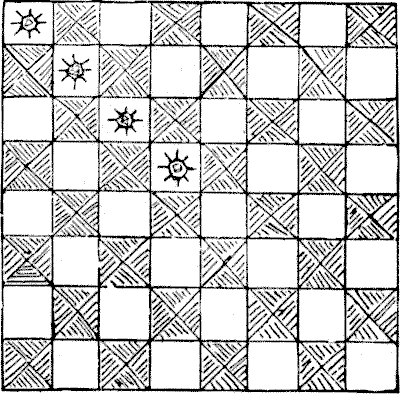 כעת הגראנד לאמה החדש היה שחקן שחמט נחות, והעדיף צורות אחרות של שעשוע תמים, כמו עריפת ראשים של אנשים. אז הוא פסל את השחמט כמשחק משפיל, שלא שיפר לא את המוח ולא את המוסר, וביטל את הטורניר באופן מיידי. ואז הוא שלח לארבעת הכמרים שהייתה להם החוצפה לשחק טוב יותר מגראנד לאמה, ופנה אליהם כדלקמן: "אנשים עלובים וכופרים, המכנים את עצמכם כמרים! האם אינכם יודעים שלטעון ליכולת לעשות משהו טוב יותר מקודמי הוא עבירה שעונשה מוות? קחו את לוח השחמט הזה ולפני שהשחר יעלה על חדר העינויים, חתכו אותו לארבעה חלקים שווים בעלי אותו צורה, שכל אחד מהם מכיל שישה עשר ריבועים מושלמים, עם אחד מהאבנים היקרות בכל חלק! אם תיכשלו בכך, אז יומצאו ספורט אחרים להנאתכם המיוחדת. לכו!" ארבעת הכמרים הצליחו במשימתם שנראתה חסרת סיכוי. האם תוכלו להראות כיצד ניתן לחלק את הלוח לארבעה חלקים שווים, שכל אחד מהם בעל אותו צורה בדיוק, על ידי חיתוכים לאורך הקווים המחלקים את הריבועים, כאשר כל חלק מכיל אחת מהאבנים היקרות?
  נושאים:

  קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 291

• משפט לוח השחמט

   

  פעם שמתי לעצמי כמשימה משעשעת לנתח לוח שחמט רגיל לאותיות האלף-בית, כך שהן ייצרו משפט שלם. ניתן לראות מהאיור שהחלקים המורכבים יוצרים את המשפט "CUT THY LIFE," עם עצירות בין המילים. המשפט האידיאלי, כמובן, היה בעל עצירה אחת בלבד, אבל לא הצלחתי להשיג זאת.

  המשפט הוא קריאה לעבריין להתנתק מחיי הרשע שהוא חי. האם תוכלו לחבר את החלקים האלה כדי ליצור לוח שחמט מושלם?

  נושאים:

  קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 294

• כשל לוח שחמט

   

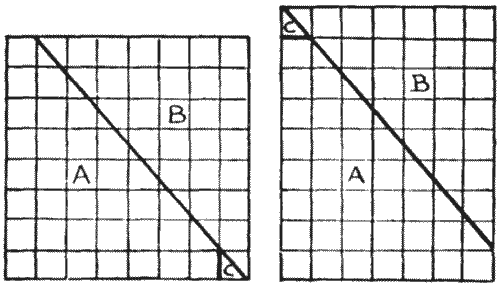
  "הנה דיאגרמה של לוח שחמט," הוא אמר. "אתם רואים שיש שישים וארבעה ריבועים—שמונה על שמונה. עכשיו אני מצייר קו ישר מהפינה השמאלית העליונה, היכן שהריבוע הראשון והשני נפגשים, אל הפינה הימנית התחתונה. אני גוזר לאורך הקו הזה עם המספריים, מחליק למעלה את החלק שסימנתי B, ואז גוזר את הפינה הקטנה C על ידי חיתוך לאורך הקו הישר הראשון. החלק הקטן הזה יתאים בדיוק למקומו למעלה, ועכשיו יש לנו מלבן עם שבעה ריבועים מצד אחד ותשעה ריבועים מצד שני. לכן, יש עכשיו רק שישים ושלושה ריבועים, מכיוון ששבע כפול תשע יוצר שישים ושלוש. לאן לעזאזל נעלם הריבוע האבוד הזה? ניסיתי שוב ושוב לתפוס את הקטן המנוול, אבל הוא תמיד מתחמק ממני. בשביל החיים שלי אני לא מצליח לגלות איפה הוא מסתתר."

  "זה נראה כמו הכשל הישן האחר של לוח השחמט, ואולי ההסבר זהה," אמר רג'ינלד—"שהחלקים לא מתאימים בדיוק."

  "אבל הם כן מתאימים," אמר הדוד ג'ון. "נסה את זה, ותראה."

  מאוחר יותר באותו ערב נראו רג'ינלד וג'ורג' בפינה כשהראשים שלהם ביחד, מנסים לתפוס את הריבוע הקטן החמקמק הזה, וזה רק הוגן לציין שלפני שהם פרשו ללילה הם הצליחו לתפוס את הטרף שלהם, אם כי חלק מחברי החברה לא הצליחו לראות אותו כשנתפס. האם הקורא יכול לפתור את התעלומה הקטנה?

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 413

• שאלה

  על נייר משבצות אינסופי מסומנות 6 משבצות, כמו בציור. על כמה משבצות נמצאות אבנים. במהלך אחד מותר לקחת אבן אם אין לו אבן שכנה מלמעלה ומימינה אז מותר לזרוק את האבן ולשים 2 אבנים במקומות מעל האבן ומימינה. האם נוכל לזרוק ע"י הפעולה הזו את כל האבנים ממקומות המסומנים אם במצב ההתחלתי האבנים היו: 
  א. (8 נקודות) בכל המשבצות המסומנות. 
  ב. (8 נקודות) רק במשבצת המסומנת הכי תחתונה והכי שמאלית. 

  O 
  O O 
  O O O

  מ. קונצוויץ' 

  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • תחרות הערים, תשמ"א, אביב, גרסה עיקרית, כיתות י"א-י"ב שאלה 5

• שאלה

  מהו המספר המקסימלי של מלכי שח שניתן להציב על לוח `8xx8`, כך שהם לא יאיימו אחד על שני?

  נושאים:

  קומבינטוריקה -> עקרון שובך היונים הוכחה ודוגמה -> בניית דוגמה קומבינטוריקה -> בדיקת מקרים -> תהליכים בעיות מינימום ומקסימום קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות

• הבונה והחפרפרת

  ישנה חלקת אדמה שצורתה ריבוע `4 times 4` המחולקת למשבצות של `1 times 1`.הבונה רוצה לבנות עליה בית שתופס 4 משבצות, שממבט על יראה כך:

  

  החפרפרת רוצה להפריע לו. למטרה זו היא יכולה לחפור בורות, שכל אחד מהם תופס משבצת אחת. אי אפשר לבנות על המשבצות שהפכו לבור. מה הוא המספר הקטן ביותר של בורות שצריכה לחפור החפרפרת, כדי שהבונה לא יוכל לבנות את הבית?

   

  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • האולימפיאדה לצעירים, תשע"ט, גמר, כיתות ג-ד שאלה 4
  • האולימפיאדה לצעירים, תשע"ט, גמר, כיתות ה-ו שאלה 2

• מגן דוד כתום

  השטח של המשולש הכחול שווה ל-1. חשבו את השטח של מגן הדוד הכתום:

  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, שלב א, כיתות ה-ו שאלה 3