קומבינטוריקה, גאומטריה קומבינטורית

גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.

• המתנה לחג המולד של גברת סמיילי

  הבעת ההנאה של גברת סמיילי הייתה כנה כאשר שש נכדותיה שלחו לה, כמתנה לחג המולד, שמיכת טלאים יפה מאוד, שהן הכינו במו ידיהן. היא נבנתה מחתיכות מרובעות של חומר משי, כולן באותו גודל, ומכיוון שהן הכינו שמיכה גדולה עם ארבעה עשר ריבועים קטנים אלה בכל צד, ברור שנתפרו לתוכה בדיוק `196` חתיכות. עכשיו, שש הנכדות תרמו כל אחת חלק מהעבודה בצורה של ריבוע מושלם (כל ששת החלקים בגודל שונה), אך כדי לחבר אותם ליצירת השמיכה המרובעת היה צורך לפרום את עבודתה של ילדה אחת לשלושה חלקים נפרדים. האם תוכלו להראות כיצד ניתן היה לבצע את החיבורים? כמובן, שאף חלק לא ניתן להפוך.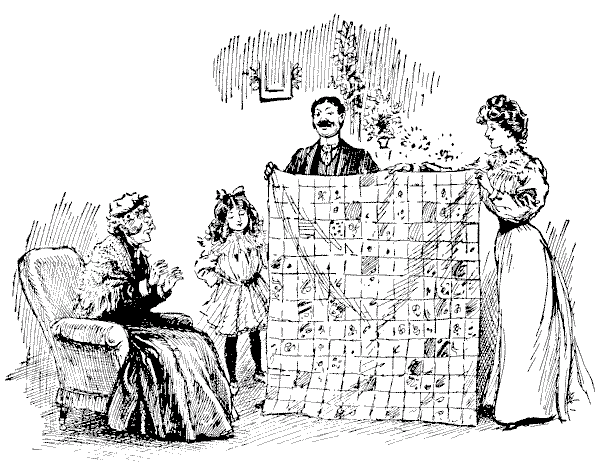
  נושאים:

  גאומטריה תורת המספרים אריתמטיקה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 172

• השמיכה של גברת פרקינס

  ניתן לראות שבמקרה זה שמיכת הטלאים המרובעת בנויה מ-`169` חלקים. החידה היא למצוא את המספר הקטן ביותר האפשרי של חלקים מרובעים שמהם יכולה להיות מורכבת השמיכה ולהראות כיצד ניתן לחבר אותם יחד. או, כדי להציג זאת הפוך, חלקו את השמיכה למספר הקטן ביותר האפשרי של חלקים מרובעים רק על ידי חיתוך התפרים.
  נושאים:

  גאומטריה -> גאומטריה במישור בעיות מינימום ומקסימום קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 173

• ריבועי הברוקד

   

  קרה שנכחתי בביתה של גברת, כאשר הרמתי משולחן שני ריבועים יפהפיים של ברוקד. הם היו דוגמאות יפהפיות של אומנות מזרחית — שניהם באותו עיצוב, דוגמה משובצת עדינה

  ."הם לא מעודנים?" אמרה חברתי. "הם הובאו לי על ידי בן דוד שחזר זה עתה מהודו. עכשיו, אני רוצה שתעניק לי קצת עזרה. אתה רואה, החלטתי לחבר אותם יחד כדי ליצור כיסוי כרית מרובע גדול אחד. איך עלי לעשות זאת כדי לשחית את החומר כמה שפחות? כמובן שאני מציעה לבצע את החתכים שלי רק לאורך הקווים שמחלקים את המשבצות הקטנות."

   

  חתכתי את שני הריבועים באופן הרצוי לארבעה חלקים שיכולים להתאים יחד וליצור ריבוע גדול יותר, תוך הקפדה על כך שהדוגמה תתאים כראוי, וכאשר סיימתי שמתי לב שלשניים מהחלקים יש בדיוק אותו שטח; כלומר, כל אחד משני החלקים הכיל את אותו מספר משבצות. האם אתה יכול להראות כיצד בוצעו החתכים בהתאם לתנאים אלה?

  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 174

• עוד חידת טלאים

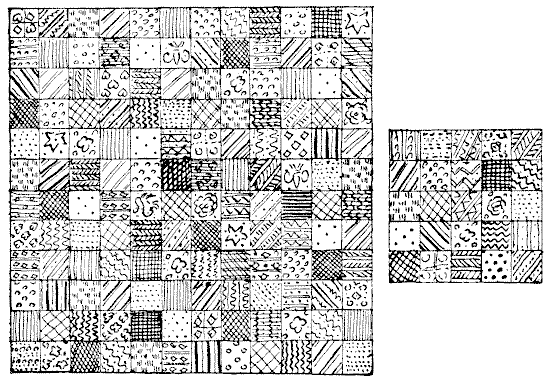  גברת קיבלה משתי חברותיה טלאי משי יפהפה, כפי שניתן לראות באיור. ניתן לראות ששני החלקים מורכבים מריבועים בגודל זהה - אחד `12x12` והשני `5x5`. היא מציעה לחבר אותם יחד וליצור שמיכת טלאים מרובעת אחת, `13x13`, אך כמובן, היא לא תחתוך אף אחד מהחומרים - רק תפרום את התפרים היכן שצריך ותחבר שוב. מה שמבלבל אותה הוא זה. חברה מבטיחה לה שלא צריך יותר מארבעה חלקים בסך הכל כדי לחבר לשמיכה החדשה. האם תוכלו להראות לה כיצד ניתן לפתור את חידת התפירה הקטנה הזו במספר כה מצומצם של חלקים?
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 175

• חיתוך לינולאום

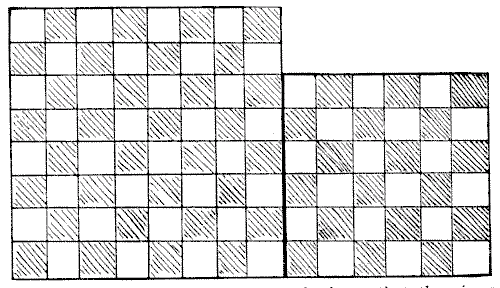  הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 176

• חידת לינולאום נוספת

   

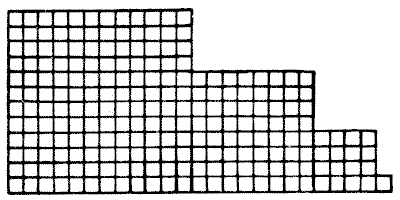
  האם תוכלו לחתוך את פיסת הלינולאום הזו לארבע חתיכות שיתאימו זו לזו וייצרו ריבוע מושלם? כמובן שהחיתוכים יכולים להתבצע רק לאורך הקווים.

  נושאים:

  גאומטריה -> גאומטריה במישור קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 177

• ארבעת הבנים

  קוראים יזהו את הדיאגרמה כחבר ותיק מימי נעוריהם. לאיש הייתה אחוזה בצורת ריבוע. הוא הוריש לאלמנתו את הרבע המוצל של האחוזה. את היתר היה צריך לחלק באופן שווה בין ארבעת בניו, כך שכל אחד יקבל קרקע באותו שטח בדיוק ובאותה צורה בדיוק. מוצג לנו איך זה נעשה. אבל המשך הסיפור אינו ידוע כל כך. במרכז האחוזה הייתה באר, המסומנת על ידי הנקודה הכהה, ובנימין, צ'ארלס ודוד התלוננו שהחלוקה אינה "הוגנת", מכיוון שלאAlfred הייתה גישה לבאר הזו, בעוד שהם לא יכלו להגיע אליה מבלי להסיג את גבולו של מישהו אחר. החידה היא להראות כיצד יש לחלק את האחוזה כך שלכל בן תהיה קרקע באותו צורה ובאותו שטח, ולכל אחד תהיה גישה לבאר מבלי לרדת מהשטח שלו.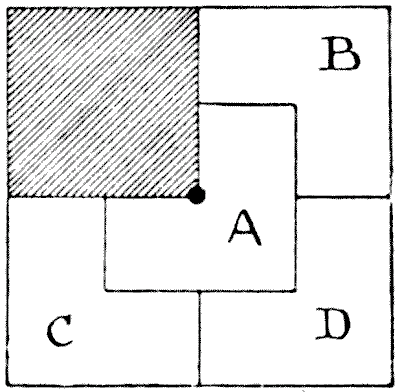
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 180

• חומות הגן

   

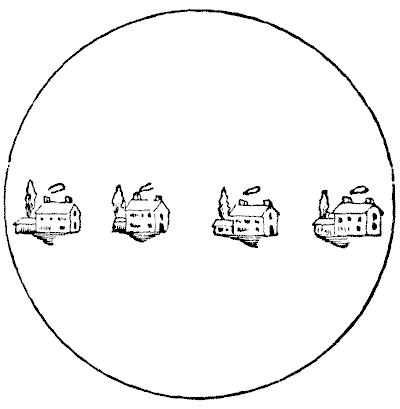
  יזם נדל"ן ספקולטיבי מחזיק בשדה עגול, עליו הקים ארבעה קוטג'ים, כפי שמוצג באיור. השדה מוקף בחומה מלבנים, והבעלים התחייב להקים עוד שלושה קירות לבנים, כך שהשכנים לא יוכלו להציץ אחד לשני, אך ארבעת הדיירים מתעקשים שלא תהיה אפליה, ושלכל אחד יהיה בדיוק אותו אורך שטח קיר לעצי הפרי שלו. החידה היא להראות כיצד ניתן לבנות את שלושת הקירות כך שלכל דייר יהיה אותו שטח אדמה, ובדיוק אותו אורך של קיר.

  כמובן, כל גן חייב להיות סגור לחלוטין על ידי קירותיו, וחייב להיות אפשרי להוכיח שלכל גן יש בדיוק אותו אורך של קיר. אם החידה נפתרת כראוי, אין צורך במספרים.

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 194

• חידת גפרורים חדשה

  באיור מוצגים שמונה-עשר גפרורים המסודרים כך שהם תוחמים שני שטחים, כאשר אחד גדול פי שניים מהשני. האם תוכלו לסדר אותם מחדש (`1`) כך שיתחמו שני שטחים מרובעים, כאשר אחד גדול בדיוק פי שלושה מהשני, ו- (`2`) כך שיתחמו שני שטחים מחומשים, כאשר אחד גדול בדיוק פי שלושה מהשני? יש להשתמש בכל שמונה-עשר הגפרורים בצורה הוגנת בכל מקרה; שני השטחים חייבים להיות מופרדים לחלוטין, ולא צריכים להיות קצוות רופפים או גפרורים כפולים.
  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים -> חידות גפרורים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 204

• מטע בבורמה

  לפני זמן קצר קיבלתי מכתב מעניין מהכומר הבריטי במייקטילה, בורמה העליונה, בו כתב לי הכומר שנהנה באונייה בדרכו לשם לנסות לפתור את החידה הקטנה הזו.

   

  אם יש לו מטע של ארבעים ותשעה עצים, נטועים בצורת ריבוע כפי שמוצג באיור המצורף, הוא רוצה לדעת איך הוא יכול לכרות עשרים ושבעה מהעצים כך שעשרים ושניים העצים שיישארו יעמדו בשורות רבות ככל האפשר עם ארבעה עצים בכל שורה.

  כמובן שלא יכולים להיות יותר מארבעה עצים בשורה.

  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 212