קומבינטוריקה, גאומטריה קומבינטורית
גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.
חתכו צורה גאומטריה על נייר משבצות-
שתי סולמיות
מהו המספר המרבי של צורות "דומינו" (מלבנים `1 times 2` או `2 times 1`) שניתן למקם בתוך הצורה הכתומה,
כך שהם לא יעלו אחד על השני ולא יחרגו מחוץ לגבולות הצורה?
מקורות:נושאים:קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> בדיקת מקרים -> תהליכים בעיות מינימום ומקסימום קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות -
היקף גדול
מציירים על נייר משבצות מצולע עם שטח 12, שכל צלעותיו עוברות על קווי המשבצות. מהו ההיקף הגדול ביותר שיכול להיות למצולע זה?
מקורות: -
ציור של קשר
נתון לוח משבצות בגודל 5x5 שמחולק למשבצות 1x1. שתי משבצות נקראות קשורות אם הן נמצאות באותה שורה או באותה עמודה, והמרחק בין מרכזי המשבצות הוא 2 או 3.
לדוגמה, בציור מסומנות בצבע אפור כל המשבצות הקשורות למשבצת האדומה. סמי מקבל לוח לבן, ורוצה לסמן עליו כמה שיותר משבצות שאף שתיים מהן אינן קשורות זו לזו. מהי הכמות המרבית של משבצות שהוא יכול לסמן?
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים בעיות מינימום ומקסימום קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- אולימפיאדת גיליס, תשע"ט שאלה 2
-
בצעדי פרש
פרש נע על גריד אינסופי. הוא מתחיל בנקודה (0,0) ועליו להגיע אל
הנקודה (5,27). בהנחה שהוא נע במספר הצעדים הקטן ביותר הנדרש,
כמה אפשרויות שונות יש לו להגיע לנקודה זו?מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות -
צפוף פה!
על לוח המשחק ממוקמים 55 גלגלי שיניים בצורת 'פירמידה':
10 גלגלים בשורה התחתונה, 9 גלגלים בזו שמעליה, וכן הלאה.
במצב זה, הגלגלים לא יכולים להסתובב בחופשיות (שכנעו את עצמכם מדוע!)
מסירים גלגלי שיניים כדי לאפשר תנועה חופשית.
כמה גלגלים לכל היותר יישארו על הלוח כך שכולם יוכלו להסתובב?
מקורות: -
שאלה
נתון לוח בגודל של 6 על 6 מרצפות ריבועיות. מרצפים אותו ב-36 מרצפות, שעל כל אחת מהן מצויירים שני רבעי מעגל המחברים את האמצעים של צלעות צמודות, כמו בציור. מהו המספר הגדול ביותר של רבעי מעגל שיכולים להתחבר לקו רציף אחד? צייר דוגמא המכילה קו כזה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות -
חידת מטעים
לאיש היתה חלקת אדמה מרובעת עם ארבעים ותשעה עצים, אך, כפי שניתן לראות מההשמטות באיור, ארבעה עצים נפלו וסולקו. כעת הוא רוצה לכרות את כל היתר מלבד עשרה עצים, שאותם יש להשאיר כך שהם ייצרו חמש שורות ישרות עם ארבעה עצים בכל שורה. אילו הם עשרת העצים שעליו להשאיר?
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 208
-
אימון טורפדו
אם צי של שישה עשר ספינות מלחמה עוגן ומוקף על ידי האויב, כמה ספינות עשויות לטבוע אם כל טורפדו, המשוגר בקו ישר, יעבור מתחת לשלוש ספינות ויטביע את הרביעית? בתרשים סידרנו את הצי במבנה ריבועי, שם ניתן לראות שאפשר להטביע עד שבע ספינות (אלו בשורה העליונה ובעמודה הראשונה) על ידי ירי הטורפדות המסומנים על ידי החצים. בעגינת הצי כרצוננו, עד כמה נוכל להגדיל את המספר הזה? זכרו שכל ספינה עוקבת טובעת לפני שיגור טורפדו נוסף, וכל טורפדו נע בכיוון אחר; אחרת, על ידי הצבת הספינות בקו ישר, אנו עשויים להטביע עד שלושה עשר! זהו מחקר קטן ומעניין בלוחמה ימית, ומעשי במיוחד - בתנאי שהאויב יאפשר לך לסדר את הצי שלו לנוחיותך ויבטיח לשכב בשקט ולא לעשות דבר!
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 235
-
מטרת הצלב
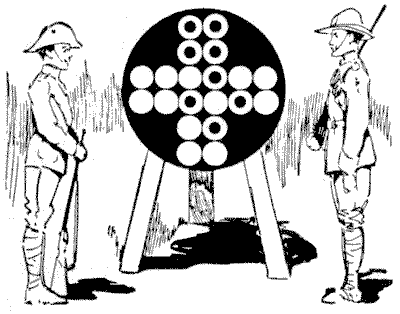באיור יש לנו מטרה מעט מוזרה שעוצבה על ידי צלף אקסצנטרי. הרעיון שלו היה שכדי לצבור ניקוד, עליך לפגוע בארבעה עיגולים בארבע יריות כך שאותן ארבע יריות ייצרו ריבוע. ניתן לראות מהתוצאות שנרשמו על המטרה ששני ניסיונות הצליחו. האדם הראשון פגע בארבעת העיגולים בראש הצלב, ובכך יצר את הריבוע שלו. האדם השני התכוון לפגוע בארבעת העיגולים בזרוע התחתונה, אך היריה השנייה שלו, בצד שמאל, הייתה גבוהה מדי. זה אילץ אותו להשלים את הארבעה שלו בצורה שונה ממה שהוא התכוון. כך ניתן לראות שלמרות שזה לא משנה באיזה עיגול אתה פוגע ביריה הראשונה, היריה השנייה עשויה לחייב אותך לנוהל מוגדר אם אתה רוצה להשיג את הריבוע שלך. כעת, החידה היא לומר בכמה דרכים שונות אפשר ליצור ריבוע על המטרה עם ארבע יריות.
מקורות:נושאים:גאומטריה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 284
-
סהרוני הירח של ביזנטיון
כאשר פיליפוס ממקדוניה, אביו של אלכסנדר הגדול, מצא עצמו ניצב בפני קשיים גדולים במצור על ביזנטיון, הוא הורה לאנשיו לחתור תחת החומות. אולם, משאלותיו סוכלו, שכן לא חלף זמן רב לאחר תחילת הפעולות, עד שסהר ירח הופיע לפתע בשמים וחשף את תוכניותיו בפני יריביו. הביזנטים שמחו מטבע הדברים, וכדי להביע את הכרת התודה שלהם הקימו פסל לדיאנה, והסהר הפך מאז לסמל המדינה. במקדש שהכיל את הפסל הייתה רצפה מרובעת שהורכבה משישים וארבעה אריחים גדולים ויקרים. כולם היו פשוטים, למעט חמישה, שנשאו את סמל הסהר. חמשת אלה הוצבו מסיבות נסתרות כך שכל אריח יהיה תחת השגחה (כלומר, בקו ישר, אנכית, אופקית או אלכסונית) של לפחות אחד מהסהרונים. הסידור שאומץ על ידי האדריכל הביזנטי היה כדלקמן:—
כעת, כיסוי אחד מחמשת הסהרונים הללו היה עבירה חמורה, שהעונש עליה היה מוות מכאיב וממושך מאוד. אבל לרגל חגיגה מסוימת היה צורך להניח על המרצפת הזו שטיח מרובע בגודל המרבי האפשרי, והראיתי באיור על ידי הצללה כהה את הממדים הגדולים ביותר שיהיו זמינים.
החידה היא להראות כיצד האדריכל, אילו חזה את שאלת השטיח הזו, יכול היה לסדר את חמשת אריחי הסהר שלו בהתאם לתנאים הנדרשים, ובכל זאת לאפשר הנחת שטיח מרובע גדול ככל האפשר מבלי שאף אחד מחמשת אריחי הסהר יכוסה, או כל חלק מהם.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 312