קומבינטוריקה, גאומטריה קומבינטורית
גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.
חתכו צורה גאומטריה על נייר משבצות-
הצלב הדרומי

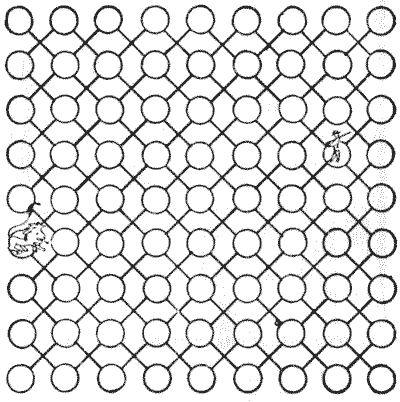
באיור לעיל יש לנו חמישה כוכבי לכת ושמונים ואחד כוכבים קבועים, כאשר חמישה מהאחרונים מוסתרים על ידי כוכבי הלכת. ניתן לראות שכל כוכב, למעט עשרת הכוכבים שיש להם נקודה שחורה במרכזם, נמצא בקו ישר, אנכית, אופקית או באלכסון, עם לפחות אחד מכוכבי הלכת. החידה היא לסדר מחדש את כוכבי הלכת כך שכל הכוכבים יהיו בקו אחד עם אחד או יותר מהם.
בסידור מחדש של כוכבי הלכת, כל אחד מחמשתם עשוי לנוע פעם אחת בקו ישר, בכל אחד משלושת הכיוונים שהוזכרו. הם, כמובן, יסתירו חמישה כוכבים אחרים במקום אלה המכוסים כעת.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 314
-
חידה עם חיילים
הנח שני חיילים באמצע לוח השחמט, אחד ב-Q `4` והשני ב-K `5`. כעת, הנח את ארבעה-עשר החיילים הנותרים (שישה-עשר בסך הכל) כך שאף שלושה לא יהיו בקו ישר בכל כיוון אפשרי.
שים לב שאני בכוונה לא אומר מלכות, מכיוון שעל ידי המילים "בכל כיוון אפשרי" אני חורג מעבר להתקפות על אלכסונים. יש להתייחס לחיילים כנקודות בלבד במרחב - במרכזי הריבועים. ראה קווים מנוקדים במקרה של מס' `300`, "שמונה מלכות."
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 317
-
ציד אריות
חברי, קפטן פות'ם הול, צייד חיות גדולות ידוע, אומר שאין דבר מלהיב יותר ממפגש עם עדר—להקה—צוות—מִשְׁפָּחָה—נחיל (לקח לי רבע שעה שלמה להיזכר במילה הנכונה, אבל סוף סוף מצאתי אותה)—גאווה של אריות. מדוע מספר אריות נקרא "גאווה," מספר לווייתנים נקרא "בית ספר," ומספר שועלים נקרא "רמייה" הן תעלומות של פילולוגיה שאליהן לא אכנס.
ובכן, הקפטן אומר שאם אריה נמרץ חוצה את דרכך במדבר, זה נהיה תוסס, כי האריה בדרך כלל חיפש את האדם בדיוק כמו שהאדם חיפש את מלך היער. ובכל זאת כשהם נפגשים הם תמיד רבים ונלחמים. קצת התבוננות בסכסוך המצער והמתמשך הזה בין שתי משפחות מכובדות הובילה אותי להבין כמה חישובים לגבי הסבירות שהאדם והאריה יחצו זה את דרכו של זה בג'ונגל. בכל המקרים הללו צריך להתחיל בהנחות מסוימות פחות או יותר שרירותיות. לכן באיור לעיל חשבתי לנכון לייצג את השבילים במדבר בסדר מופתי כזה. למרות שהקפטן מבטיח לי שעקבות האריות בדרך כלל רצים בדרך הזו, יש לי ספקות.
החידה היא פשוט לגלות בכמה דרכים שונות ניתן להציב את האדם והאריה בשני מקומות שונים שאינם על אותו נתיב. על ידי "נתיבים" יש להבין שאני מתייחס רק לקווים המצוירים. לפיכך, למעט ארבע הנקודות הפינתיות, כל לוחם נמצא תמיד בשני נתיבים ולא יותר. ניתן לראות שיש הרבה מקום להתחמק זה מזה במדבר, וזה בדיוק מה שתמיד הבינו.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 318
-
מסע הצריח
אני קורא לחידה הזו "מסע הצריח", מכיוון שהמילה "tour" (הנגזרת מגלגל של חרט) מרמזת שאנו חוזרים לנקודה ממנה יצאנו, ואנו לא עושים זאת במקרה הזה. לא נהיה מרוצים מסיור חג מודרך אישית שהסתיים בכך שהשאיר אותנו, למשל, באמצע הסהרה. הצריח כאן עושה עשרים ואחד מהלכים, שבמהלכם הוא מבקר בכל משבצת בלוח פעם אחת בלבד, ועוצר במשבצת המסומנת `10` בסוף המהלך העשירי שלו, ומסתיים במשבצת המסומנת `21`. שני מהלכים רצופים אינם יכולים להתבצע באותו כיוון - כלומר, עליך לבצע פנייה לאחר כל מהלך.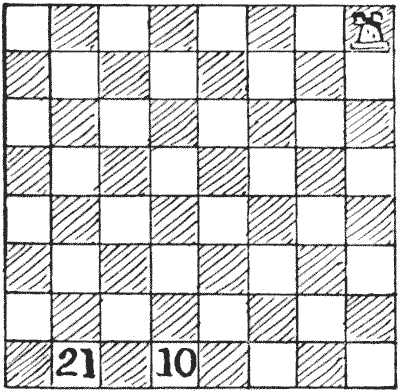 מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 321
-
מרוץ היאכטות
ובכן, יא יבשושים, הניפו את המפרשים הקדמיים הקטנים שלכם, שלפו את הספינקרים, שחררו את יריעות הבלון והכינו את מפרשי הראש שלכם!
המרוץ שלנו מורכב מלהתחיל מהנקודה שבה היאכטה נמצאת באיור ולגעת בכל אחד משישים וארבעת המצופים בארבעה-עשר מסלולים ישרים, ולחזור בזיגזג הסופי למצוף ממנו התחלנו. המסלול השביעי חייב להסתיים במצוף שעליו מתנוסס דגל.
חידה זו תדרוש מיומנות ימית רבה בשל הזוויות החדות שבהן יהיה צורך לעיתים לעשות זיגזג. חוד של עיפרון ועין ימית טובה הם כל הציוד שאנו זקוקים לו.
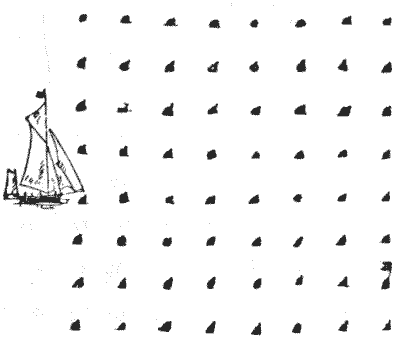
זה קשה, בגלל התנאי לגבי מצוף הדגל, ובגלל שזהו מסלול חוזר. אבל שוב מותרים לנו הקווים האלכסוניים האלה.
מקורות:נושאים:גאומטריה -> גאומטריה במישור -> חשבון זוויות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 330
-
סנט ג'ורג' והדרקון
 הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת.
מקורות:
הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 334
-
שדות התירס של החוואי לורנס
אחד האזורים היפים ביותר בקרבת לונדון לטיול קיץ הוא אותו חלק של בקינגהאמשייר המכונה עמק הצ'ס—לפחות, כך היה לפני כמה שנים, לפני שנתגלה על ידי הקבלן הספקולטיבי. בתחילת המאה הנוכחית חי, לא רחוק מלטיימרס, חקלאי מכובד אך תמהוני בשם לורנס. אחד הרעיונות המוזרים שלו היה שכל אדם שגר ליד גדות נהר הצ'ס צריך להיות בדרך כלשהי בקיא במשחק האצילי באותו שם, וכדי להטביע עובדה זו על אנשיו ושכניו הוא אימץ לעתים טרמינולוגיה מוזרה. לדוגמה, כאשר אחת הכבשות שלו הציגה לו טלה, הוא היה אומר שהיא "הכתירה רגלי"; כאשר הוא הקים אסם חדש מול הכביש המהיר, הוא כינה זאת "הצרחה בצד המלך"; וכאשר הוא שלח אדם עם אקדח כדי להרחיק את הציפורים של שכנו משדותיו, הוא דיבר על זה כ"תקיפת הצריחים של יריבו". כולם בשכונה נהגו להתבדר מהבדיחות הקטנות של החוואי לורנס, ונער אחד (הליצן של הכפר) שספג משיכות אוזניים מהג'נטלמן הזקן על שגנב את ה"ערמונים" שלו הרחיק לכת עד כדי כך שכינה אותו "מגן שחמט זקן ומטופש!"
באחת השנים היה לו שדה מרובע גדול המחולק לארבעים ותשעה מגרשים מרובעים, כפי שמוצג באיור. הריבועים הלבנים נזרעו בחיטה והריבועים השחורים בשעורה. כשמגיע זמן הקציר הוא נתן הוראה שאנשיו יחתכו תחילה את התירס בחלקה המסומנת `1`, וכי כל חיתוך עוקב יהיה בדיוק מהלך פרש מהאחרון, החיתוך השלושה עשר יהיה בחלקה המסומנת `13`, העשרים וחמישי בחלקה המסומנת `25`, השלושים ושבעה בזו המסומנת `37`, והאחרון, או ארבעים ותשעה, בחלקה המסומנת `49`. זה היה יותר מדי עבור הודג' המסכן, ובכל יום החוואי לורנס היה צריך לרדת לשדה ולהראות על איזה חלק צריך להפעיל. אבל הבעיה אולי לא תציג קושי לקוראים שלי.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 335
-
ארבעת הקנגורו
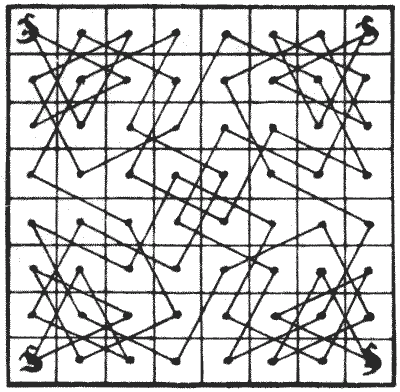 בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.
בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.החידה היא פשוטה. בוקר אחד כל קנגורו יצא לקפיצת הבוקר שלו, ובשש עשרה קפיצות פרש רצופות ביקר בחמישה עשר שדות שונים וחזר לפינה שלו. אף שדה לא ביקר על ידי יותר מאחד הקנגורו. הדיאגרמה מראה כיצד הם הסדירו את העניינים. מה שמבקשים מכם לעשות הוא להראות כיצד הם יכלו לבצע את המעשה מבלי שאף קנגורו יחצה את הקו האופקי באמצע הריבוע שמחלק את הלוח לשני חלקים שווים.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 337
-
מסע הפרש הקסום
הנה בעיה שעדיין לא נפתרה, וגם לא הוכחה אי-אפשרותה. שחקו עם הפרש פעם אחת בכל משבצת בלוח השחמט במסע שלם, ספרו את המשבצות לפי סדר הביקור, כך שכאשר תושלם, הריבוע יהיה "קסום," ויסתכם ל-`260` בכל טור, בכל שורה ובכל אחד משני האלכסונים הארוכים. אתן את התשובה הטובה ביותר שהצלחתי להשיג, שבה יש טעות קלה באלכסונים בלבד. האם ניתן למצוא פתרון מושלם? אני משוכנע שאי אפשר, אבל זו רק "דעה נלהבת."
מקורות:נושאים:לוגיקה קומבינטוריקה -> טבלאות מספריות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 412