קומבינטוריקה, בדיקת מקרים, תהליכים
קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.
-
שלוש הכבשים
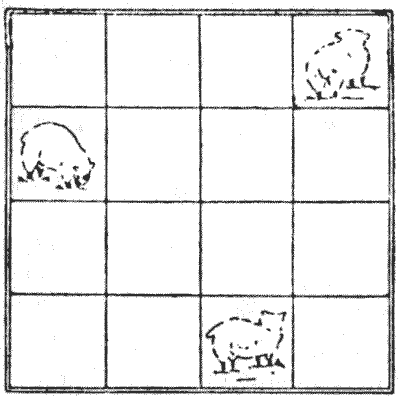 לחקלאי היו שלוש כבשים וסידור של שש עשרה מכלאות, המחולקות על ידי גדרות באופן המצוין באיור. בכמה דרכים שונות הוא יכול למקם את הכבשים האלה, כל אחת במכלאה נפרדת, כך שכל מכלאה תהיה מאוכלסת או בשורה (אופקית, אנכית או אלכסונית) עם כבשה אחת לפחות? נתתי סידור אחד שמקיים את התנאים. כמה אחרים אתה יכול למצוא? אין לספור היפוכים ושיקופים כדברים שונים. הקורא רשאי להתייחס לכבשים כמלכות. הבעיה היא אז למקם את שלוש המלכות כך שכל משבצת תהיה מאוכלסת או מותקפת על ידי מלכה אחת לפחות - במספר המרבי של דרכים שונות.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
לחקלאי היו שלוש כבשים וסידור של שש עשרה מכלאות, המחולקות על ידי גדרות באופן המצוין באיור. בכמה דרכים שונות הוא יכול למקם את הכבשים האלה, כל אחת במכלאה נפרדת, כך שכל מכלאה תהיה מאוכלסת או בשורה (אופקית, אנכית או אלכסונית) עם כבשה אחת לפחות? נתתי סידור אחד שמקיים את התנאים. כמה אחרים אתה יכול למצוא? אין לספור היפוכים ושיקופים כדברים שונים. הקורא רשאי להתייחס לכבשים כמלכות. הבעיה היא אז למקם את שלוש המלכות כך שכל משבצת תהיה מאוכלסת או מותקפת על ידי מלכה אחת לפחות - במספר המרבי של דרכים שונות.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 310
-
חידת חמשת הכלבים
בשנת `1863`, סי. אף. דה יאניש דן לראשונה ב"חידת חמש המלכות" - להציב חמש מלכות על לוח השחמט כך שכל משבצת תותקף או תאוכלס - אשר הוצעה על ידי חברו, "מר דה ר.". יאניש הראה שאם אף מלכה לא יכולה לתקוף מלכה אחרת, ישנן תשעים ואחת דרכים שונות להציב את חמש המלכות, כאשר היפוכים ושיקופים אינם נחשבים כשונים. אם המלכות יכולות לתקוף זו את זו, תיעדתי מאות דרכים, אך לא ניתן למנות אותן במדויק.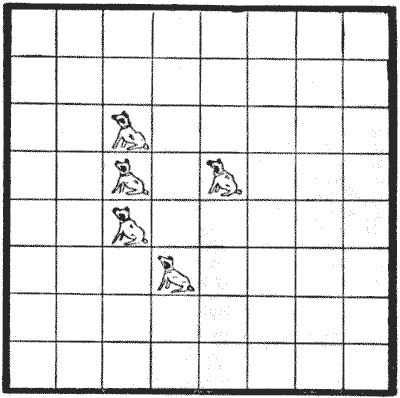 האיור אמור לייצג סידור של שישים וארבעה מְלוּנוֹת. ניתן לראות שחמש מְלוּנוֹת מכילות כל אחת כלב, ובבדיקה נוספת ניתן לראות שכל אחת משישים וארבע המְלוּנוֹת נמצאת בקו ישר עם לפחות כלב אחד - או אופקית, אנכית או באלכסון. קח כל מְלוּנָה שתרצה, ותגלה שתוכל למתוח קו ישר לכלב באחת משלוש הדרכים שהוזכרו. החידה היא להחליף את חמשת הכלבים ולגלות בכמה דרכים שונות ניתן להציב אותם בחמש מְלוּנוֹת בשורה ישרה, כך שכל מְלוּנָה תמיד תהיה בקו אחד עם לפחות כלב אחד. היפוכים ושיקופים נחשבים כאן כשונים.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
האיור אמור לייצג סידור של שישים וארבעה מְלוּנוֹת. ניתן לראות שחמש מְלוּנוֹת מכילות כל אחת כלב, ובבדיקה נוספת ניתן לראות שכל אחת משישים וארבע המְלוּנוֹת נמצאת בקו ישר עם לפחות כלב אחד - או אופקית, אנכית או באלכסון. קח כל מְלוּנָה שתרצה, ותגלה שתוכל למתוח קו ישר לכלב באחת משלוש הדרכים שהוזכרו. החידה היא להחליף את חמשת הכלבים ולגלות בכמה דרכים שונות ניתן להציב אותם בחמש מְלוּנוֹת בשורה ישרה, כך שכל מְלוּנָה תמיד תהיה בקו אחד עם לפחות כלב אחד. היפוכים ושיקופים נחשבים כאן כשונים.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 311
-
סהרוני הירח של ביזנטיון
כאשר פיליפוס ממקדוניה, אביו של אלכסנדר הגדול, מצא עצמו ניצב בפני קשיים גדולים במצור על ביזנטיון, הוא הורה לאנשיו לחתור תחת החומות. אולם, משאלותיו סוכלו, שכן לא חלף זמן רב לאחר תחילת הפעולות, עד שסהר ירח הופיע לפתע בשמים וחשף את תוכניותיו בפני יריביו. הביזנטים שמחו מטבע הדברים, וכדי להביע את הכרת התודה שלהם הקימו פסל לדיאנה, והסהר הפך מאז לסמל המדינה. במקדש שהכיל את הפסל הייתה רצפה מרובעת שהורכבה משישים וארבעה אריחים גדולים ויקרים. כולם היו פשוטים, למעט חמישה, שנשאו את סמל הסהר. חמשת אלה הוצבו מסיבות נסתרות כך שכל אריח יהיה תחת השגחה (כלומר, בקו ישר, אנכית, אופקית או אלכסונית) של לפחות אחד מהסהרונים. הסידור שאומץ על ידי האדריכל הביזנטי היה כדלקמן:—

כעת, כיסוי אחד מחמשת הסהרונים הללו היה עבירה חמורה, שהעונש עליה היה מוות מכאיב וממושך מאוד. אבל לרגל חגיגה מסוימת היה צורך להניח על המרצפת הזו שטיח מרובע בגודל המרבי האפשרי, והראיתי באיור על ידי הצללה כהה את הממדים הגדולים ביותר שיהיו זמינים.
החידה היא להראות כיצד האדריכל, אילו חזה את שאלת השטיח הזו, יכול היה לסדר את חמשת אריחי הסהר שלו בהתאם לתנאים הנדרשים, ובכל זאת לאפשר הנחת שטיח מרובע גדול ככל האפשר מבלי שאף אחד מחמשת אריחי הסהר יכוסה, או כל חלק מהם.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 312
-
חידת מלכות ורץ
יובחן שכל משבצת בלוח היא תפוסה או מותקפת. החידה היא להחליף רץ בצריח באותה המשבצת, ואז להניח את ארבע המלכות על משבצות אחרות כך שכל משבצת שוב תהיה תפוסה או מותקפת.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 313
-
חידת יתדות הכובעים
הנה חידה בת חמש מלכות שהצגתי בצורה דמיונית בשנת `1897`. מכיוון שהמלכות יוצגו שם ככובעים על שישים וארבעה יתדות, אדבוק בכותרת, "חידת יתדות הכובעים". ניתן לראות שכל משבצת מאוכלסת או מותקפת. החידה היא להעביר מלכה אחת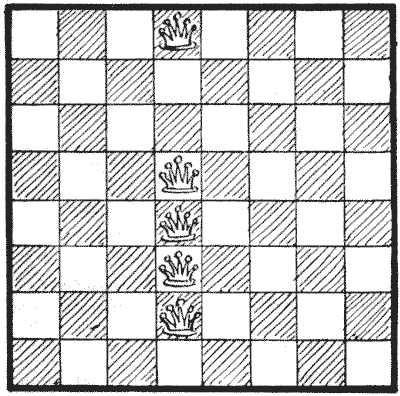 למשבצת אחרת כך שעדיין כל משבצת תהיה מאוכלסת או מותקפת, לאחר מכן להעביר מלכה שנייה בתנאים דומים, לאחר מכן מלכה שלישית, ולבסוף מלכה רביעית. לאחר המסע הרביעי כל משבצת חייבת להיות מותקפת או מאוכלסת, אך אף מלכה לא תתקוף מלכה אחרת. כמובן, שהמסעים לא חייבים להיות "מסעי מלכה"; ניתן להעביר מלכה לכל חלק בלוח.
מקורות:
למשבצת אחרת כך שעדיין כל משבצת תהיה מאוכלסת או מותקפת, לאחר מכן להעביר מלכה שנייה בתנאים דומים, לאחר מכן מלכה שלישית, ולבסוף מלכה רביעית. לאחר המסע הרביעי כל משבצת חייבת להיות מותקפת או מאוכלסת, אך אף מלכה לא תתקוף מלכה אחרת. כמובן, שהמסעים לא חייבים להיות "מסעי מלכה"; ניתן להעביר מלכה לכל חלק בלוח.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 315
-
שומרי האבירים
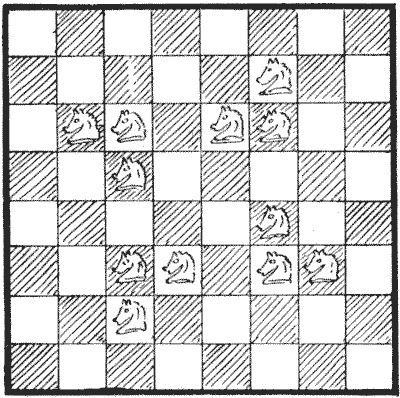
האביר הוא הקומיקאי הנמוך חסר האחריות של לוח השחמט. "הוא נוכל מאוד לא בטוח, מתגנב ומדכא," אומר סופר אמריקאי. "הוא יכול לזוז רק שני ריבועים, אך מפצה על כמות התנועה שלו באיכותה, שכן הוא יכול לקפוץ ריבוע אחד הצידה ואחד קדימה בו זמנית, כמו חתול; יכול לעמוד על רגל אחת באמצע הלוח ולקפוץ לכל אחד משמונת הריבועים שהוא בוחר; יכול לעלות על צד אחד של גדר ולהשמיץ שלושה או ארבעה אנשים בצד השני; יש לו דרך מעוררת התנגדות להכניס את עצמו למקומות בטוחים שבהם הוא יכול להפחיד את המלך ולאלץ אותו לזוז, ואז לטרוף מלכה. לרוע טהור אין לאביר שווה, וכאשר אתה רודף אחריו מחור אחד הוא קופץ לאחר." נעשו ניסיונות שוב ושוב להשיג הגדרה קצרה, פשוטה ומדויקת של תנועת האביר—ללא הצלחה. זה באמת מורכב מלהזיז ריבוע אחד כמו צריח, ואז ריבוע אחר כמו רץ—שני הפעולות נעשות בקפיצה אחת, כך שלא משנה אם הריבוע הראשון שעוברים עליו תפוס על ידי כלי אחר או לא. זו, למעשה, התנועה הקופצת היחידה בשחמט. אבל קשה ככל שיהיה להגדיר, ילד יכול ללמוד את זה על ידי הסתכלות תוך מספר דקות.
הראיתי בתרשים כיצד ניתן להציב שנים עשר אבירים (המספר הקטן ביותר האפשרי שיבצע את המשימה) על לוח השחמט כך שכל ריבוע יהיה או תפוס או מותקף על ידי אביר. בחן כל ריבוע בתורו, ותגלו שזה כך. כעת, החידה במקרה זה היא לגלות מהו המספר הקטן ביותר האפשרי של אבירים הנדרש כדי שכל ריבוע יהיה או תפוס או מותקף, וכל אביר מוגן על ידי אביר אחר. ואיך הייתם מסדרים אותם? יתברר שמתוך שנים עשר המוצגים בתרשים רק ארבעה מוגנים כך על ידי היותם במרחק מהלך של אביר מאביר אחר.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 319
-
מסע הצריח
אני קורא לחידה הזו "מסע הצריח", מכיוון שהמילה "tour" (הנגזרת מגלגל של חרט) מרמזת שאנו חוזרים לנקודה ממנה יצאנו, ואנו לא עושים זאת במקרה הזה. לא נהיה מרוצים מסיור חג מודרך אישית שהסתיים בכך שהשאיר אותנו, למשל, באמצע הסהרה. הצריח כאן עושה עשרים ואחד מהלכים, שבמהלכם הוא מבקר בכל משבצת בלוח פעם אחת בלבד, ועוצר במשבצת המסומנת `10` בסוף המהלך העשירי שלו, ומסתיים במשבצת המסומנת `21`. שני מהלכים רצופים אינם יכולים להתבצע באותו כיוון - כלומר, עליך לבצע פנייה לאחר כל מהלך.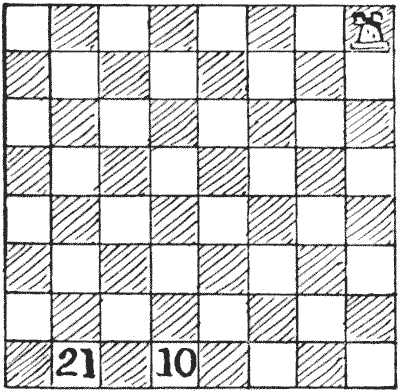 מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 321
-
חידת הגרייהאונד
בחידה זו, עשרים המכלאות אינן מתקשרות זו עם זו באמצעות דלתות, אלא מחולקות על ידי קיר נמוך. הדייר הבודד הוא הגרייהאונד שגר במכלאה בפינה השמאלית העליונה. כאשר ניתנת לו החופש, עליו להשיג אותו על ידי ביקור בכל מכלאה פעם אחת בלבד בסדרת מהלכי פרש, תוך סיום בפינה הימנית התחתונה, הפתוחה לעולם. הקווים בדיאגרמה לעיל מראים פתרון אחד. החידה היא לגלות בכמה דרכים שונות יכול הגרייהאונד לצאת כך ממכלאת הפינה שלו.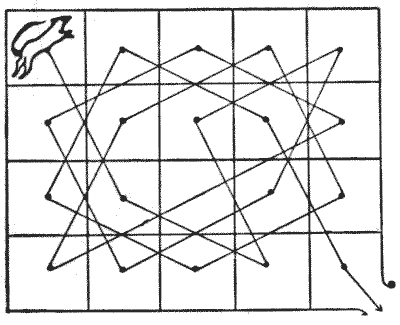 מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 336
-
ארבעת הקנגורו
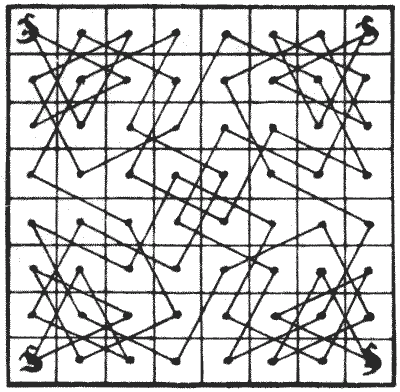 בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.
בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.החידה היא פשוטה. בוקר אחד כל קנגורו יצא לקפיצת הבוקר שלו, ובשש עשרה קפיצות פרש רצופות ביקר בחמישה עשר שדות שונים וחזר לפינה שלו. אף שדה לא ביקר על ידי יותר מאחד הקנגורו. הדיאגרמה מראה כיצד הם הסדירו את העניינים. מה שמבקשים מכם לעשות הוא להראות כיצד הם יכלו לבצע את המעשה מבלי שאף קנגורו יחצה את הקו האופקי באמצע הריבוע שמחלק את הלוח לשני חלקים שווים.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 337
-
תרגיל לאסירים
להלן תוכנית האגף הצפוני של בית סוהר מסוים, המציגה את ששת-עשר התאים שכולם מתקשרים באמצעות פתחי דלתות פתוחים. חמישה-עשר אסירים מוספרו וסודרו בתאים כפי שמוצג. הורשה להם להחליף את תאיהם ככל שרצו, אך אם שני אסירים היו אי פעם באותו תא יחד, הובטח להם עונש חמור.
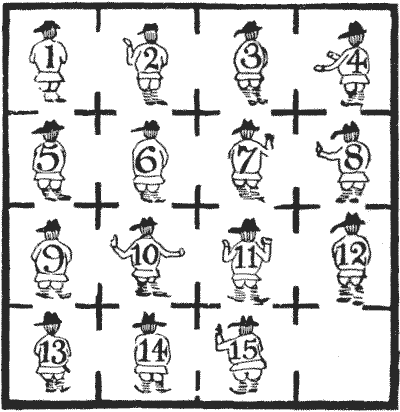
כעת, על מנת להפחית את השמנת היתר הגוברת שלהם, ולשלב פעילות גופנית עם בילוי מנטלי, החליטו האסירים, בהצעתו של אחד ממספרם שהתעניין במסעי פרשים, לנסות ליצור לעצמם מסלול פרשים מושלם מבלי להפר את תקנות הכלא, ולהשאיר את תא הפינה הימנית התחתונה ריק, כפי שהיה במקור. הבדיחה בעניין היא שהסידור אליו הגיעו היה כדלקמן:—
8 3 12 1 11 14 9 6 4 7 2 13 15 10 5 >הסוהרים לא הצליחו לזהות את העובדה החשובה שהגברים לא יכלו להגיע למצב הזה בלי ששניים מהם היו באיזשהו זמן באותו תא ביחד. נסו זאת עם אסימונים על דיאגרמה משורטטת, ותגלו שזה המצב. אחרת, הפתרון נכון מספיק, כאשר כל חבר נמצא, כנדרש, בתנועת פרש מהמספר הקודם, ותא הפינה המקורי ריק.
החידה היא להתחיל כשהגברים ממוקמים כפי באיור ולהראות כיצד ניתן היה לעשות זאת במספר המהלכים המועט ביותר, תוך מתן מנוחה מלאה למספר האסירים הרב ביותר.
מכיוון שמעולם אין יותר מתא ריק אחד עבור אדם להיכנס אליו, יש צורך רק לרשום את מספרי האנשים בסדר שבו הם נעים. ברור שמעט מאוד אנשים יכולים להישאר בתאים שלהם מבלי להפריע להם, אך אשאיר את הפותר לגלות כמה בדיוק, מכיוון שזה חלק מהותי מאוד מהחידה.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 343