קומבינטוריקה, בדיקת מקרים, תהליכים

קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.

  • ארבעה בולי דואר

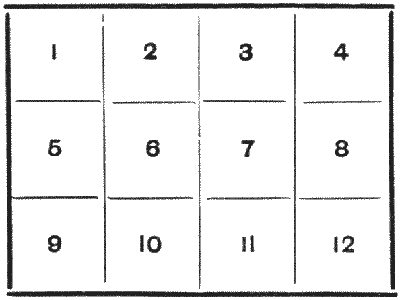    "זה קל כמו לספור", הוא ביטוי שאדם שומע לעתים. אבל ספירה פשוטה עשויה להיות מבלבלת לעתים. קחו את הדוגמה הפשוטה הבאה. נניח שזה עתה קניתם שנים-עשר בולי דואר, בצורה הזו - שלושה על ארבעה - וחבר מבקש מכם להואיל בטובכם לתת לו ארבעה בולים, כולם מחוברים יחד - בלי שאף בול יהיה תלוי רק בפינה. בכמה דרכים שונות אפשר לתלוש את ארבעת הבולים האלה? אתם רואים, אתם יכולים לתת לו `1, 2, 3, 4`, או `2, 3, 6, 7`, או `1, 2, 3, 6`, או `1, 2, 3, 7`, או `2, 3, 4, 8`, וכן הלאה. האם תוכלו לספור את מספר הדרכים השונות בהן ניתן למסור את ארבעת הבולים האלה? אין הרבה יותר מחמישים דרכים, אז זה לא ספירה גדולה. האם תוכלו לקבל את המספר המדויק? מקורות:

  • חלוקות לוח שחמט

    לאחרונה שאלתי את עצמי את השאלה: בכמה דרכים שונות ניתן לחלק לוח שחמט לשני חלקים באותו גודל וצורה על ידי חתכים לאורך הקווים המחלקים את הריבועים? עד מהרה התברר שהבעיה מרתקת ומלאת קשיים. אני מציג אותה בצורה פשוטה, תוך שימוש בלוח בעל ממדים קטנים יותר. ברור שלוח של ארבעה ריבועים יכול להיות מחולק רק בדרך אחת - על ידי חיתוך ישר במרכז - מכיוון שלא נספור היפוכים ושיקופים כשונים. במקרה של לוח של שישה עשר ריבועים - ארבעה על ארבעה - יש בדיוק שש דרכים שונות. נתתי את כולן בתרשים, והקורא לא ימצא אחרות. כעת, קחו את הלוח הגדול יותר של שלושים ושישה ריבועים, ונסו לגלות בכמה דרכים ניתן לחתוך אותו לשני חלקים באותו גודל וצורה. מקורות:

  • החלון של האב המנזר

    לפני שנים רבות, האב המנזר מסנט אדמונדסברי, כתוצאה מ"מסירות חזקה מדי לראשו," חלה ולא היה מסוגל לעזוב את מיטתו. כששכב ער, מטלטל את ראשו באי שקט מצד לצד, הנזירים הקשובים הבחינו שמשהו מטריד את מחשבותיו; אך איש לא העז לשאול מה זה יכול להיות, כי האב המנזר היה בעל אופי קשוח, ומעולם לא סבל סקרנות. לפתע קרא לאב ג'ון, והנזיר המכובד ההוא מיהר למיטתו.

    "אב ג'ון," אמר האב המנזר, "האם אתה יודע שנולדתי לעולם הנורא הזה בערב חג המולד?

    "הנזיר הנהן בהסכמה.

    "והאם לא אמרתי לך לעתים קרובות, שנולדתי בערב חג המולד, שאין לי אהבה לדברים שהם אי-זוגיים? תסתכל שם!"

     

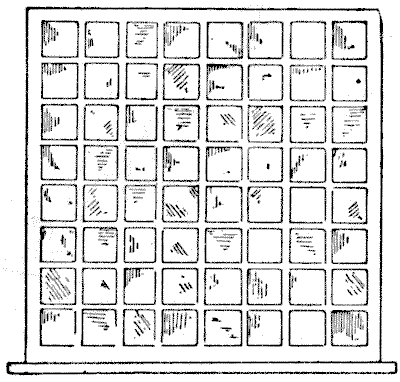
    האב המנזר הצביע על חלון המעונות הגדול, שממנו אני נותן סקיצה. הנזיר הביט, והיה נבוך.

    "האם אינך רואה ששישים וארבעת האורות מסתכמים למספר זוגי אנכית ואופקית, אך כל הקווים האלכסוניים, למעט ארבעה עשר, הם מספר שהוא אי-זוגי? מדוע זה?"

    "אכן, אדוני האב המנזר, זה טבע הדברים, ואי אפשר לשנות זאת."

    "לא, אבל זה יש ישתנה. אני מצווה עליך שחלק מהאורות ייחסמו היום, כך שלכל קו יהיה מספר זוגי של אורות. ראה שזה נעשה ללא דיחוי, שמא המרתפים יינעלו לחודש וצרות קשות אחרות יפקדו אותך."

    אב ג'ון היה חסר אונים, אך לאחר התייעצות עם מישהו שהיה בקיא בתעלומות מוזרות, נמצאה דרך לספק את גחמתו של האב המנזר. אילו אורות נחסמו, כך שאלה שנותרו הסתכמו למספר זוגי בכל קו אופקית, אנכית ואלכסונית, תוך גרימת ההפרעה המינימלית האפשרית לאור?

    מקורות:

  • לוח השחמט הסיני

    לאיזה מספר גדול של חלקים שונים ניתן לחתוך את לוח השחמט (על ידי חיתוכים לאורך הקווים בלבד), כך שלא יהיו שני חלקים זהים לחלוטין? זכרו שסידור השחור והלבן מהווה הבדל. כך, ריבוע שחור בודד יהיה שונה מריבוע לבן בודד, שורה של שלושה המכילה שני ריבועים לבנים תהיה שונה משורה של שלושה המכילה שני ריבועים שחורים, וכן הלאה. אם לא ניתן להניח שני חלקים על השולחן כך שיהיו זהים לחלוטין, הם נחשבים לשונים. ומכיוון שגב הלוח חלק, לא ניתן להפוך את החלקים. מקורות:

  • שמונת הכוכבים

    החידה במקרה הזה היא למקם שמונה כוכבים בדיאגרמה כך שאף כוכב לא יהיה באותו קו עם כוכב אחר אופקית, אנכית או אלכסונית. כוכב אחד כבר ממוקם, ואסור להזיז אותו, כך שנשארו רק שבעה לקורא למקם. אבל אסור למקם כוכב על אף אחד מהריבועים המוצללים. יש רק דרך אחת לפתור את החידה הקטנה הזו. מקורות:

  • מתחת לצעיף

    אם הקורא יבחן את הדיאגרמה לעיל, הוא יראה שמיקמתי שמונה אותיות V, שמונה אותיות E, שמונה אותיות I ושמונה אותיות L בדיאגרמה כך שאף אות אינה נמצאת בקו אחד עם אות דומה לה אופקית, אנכית או אלכסונית. לכן, אף V אינו בקו אחד עם V אחר, אף E עם E אחרת, וכן הלאה. ישנן דרכים רבות ושונות לסדר את האותיות בתנאי זה. החידה היא למצוא סידור שמניב את המספר הגדול ביותר האפשרי של מילים בנות ארבע אותיות, בקריאה מלמעלה למטה ומלמטה למעלה, אחורה וקדימה, או באלכסון. כל החזרות נחשבות למילים שונות, וחמשת הוריאציות שניתן להשתמש בהן הן: VEIL, VILE, LEVI, LIVE ו-EVIL.

    זה יובהר לחלוטין כשאומר שהסידור לעיל מקבל ניקוד של שמונה, מכיוון שהשורה העליונה והתחתונה נותנות שתיהן VEIL; הטורים השני והשביעי נותנים שתיהן VEIL; ושני האלכסונים, החל מה-L בשורה החמישית וה-E בשורה השמינית, נותנים שתיהן LIVE ו-EVIL. לכן ישנן שמונה קריאות שונות של המילים בסך הכל.

    חידת מילים קשה זו ניתנת כדוגמה לשימוש בניתוח לוח שחמט בפתרון דברים כאלה. רק אדם שמכיר את בעיית "שמונה המלכות" יכול לקוות לפתור אותה.

    מקורות:

  • הריבוע של באשה

    אחת מחידות הקלפים העתיקות ביותר היא של קלוד קספר באשה דה מז'יריאק, שפורסמה לראשונה, אני מאמין, במהדורת `1624` של עבודתו. סדרו מחדש את שישה-עשר קלפי הפנים (כולל האסים) בריבוע כך שבשום שורה של ארבעה קלפים, אופקית, אנכית או אלכסונית, לא יימצאו שני קלפים מאותה צורה או מאותו ערך. זה כשלעצמו די קל, אך נקודה בחידה היא למצוא בכמה דרכים שונות ניתן לעשות זאת. המתמטיקאי הצרפתי הדגול א. לאבוסן, במהדורה המודרנית שלו לבאשה, נותן את התשובה בצורה שגויה. ובכל זאת החידה ממש די קלה. כל סידור מייצר עוד שבעה על ידי סיבוב הריבוע והשתקפותו במראה. באשה מחשיב אותם כשונים זה מזה.

    שימו לב ל"שורה של ארבעה קלפים", כך שהאלכסונים היחידים שעלינו להתייחס אליהם כאן הם שני הארוכים.

    מקורות:

  • קוביות האותיות - שלושים ושש

    האיור מייצג קופסה המכילה שלושים ושש קוביות אותיות. החידה היא לסדר מחדש את הקוביות כך שאף A לא יהיה בקו אנכי, אופקי או אלכסוני עם A אחר, אף B עם B אחר, אף C עם C אחר, וכן הלאה. תגלו שאי אפשר להכניס את כל האותיות לקופסה בתנאים אלה, אך העניין הוא למקם כמה שיותר. כמובן שאסור להשתמש באותיות אחרות מלבד אלה המוצגות. מקורות:

  • לוח השחמט הצפוף

    החידה היא לסדר מחדש את חמישים ואחד הכלים על לוח השחמט כך שאף מלכה לא תתקוף מלכה אחרת, אף צריח לא יתקוף צריח אחר, אף רץ לא יתקוף רץ אחר, ואף פרש לא יתקוף פרש אחר. אין להתחשב בהתערבותם של כלים מסוג אחר מאלה הנדונים - כלומר, שתי מלכות ייחשבו כתוקפות זו את זו, למרות שייתכן שיהיו, למשל, צריח, רץ ופרש ביניהן. וכך גם לגבי הצריחים והרצים. אין זה קשה להיפטר מכל סוג של כלי בנפרד; הקושי נובע כאשר צריך למצוא מקום לכל הסידורים על הלוח בו זמנית. מקורות:

  • אומנות ליקוק הבולים העדינה

    חוק הביטוח הוא מקור פורה ביותר לפאזלים משעשעים, במיוחד משעשעים אם אתה במקרה נמנה עם הפטורים. ההקדמה של אדם לאומנות ליקוק הבולים העדינה מעלה את החידה הקטנה הבאה: אם יש לך כרטיס המחולק לשישה עשר מקומות (`4` × `4`), ומסופקים לך שפע של בולים בערכים של `1`d., `2`d., `3`d., `4`d., ו-`5`d., מהו הערך הגדול ביותר שתוכל להדביק על הכרטיס אם שר האוצר אוסר עליך להניח בול בקו ישר (כלומר, אופקית, אנכית או אלכסונית) עם בול אחר בעל ערך דומה? כמובן, ניתן להדביק רק בול אחד במקום אחד. הקורא כנראה יגלה, כשהוא יראה את הפתרון, שבדומה לבולים עצמם, הוא הוכה. סביר להניח שיחסרו לו שני פני מהמקסימום. חבר שאל את הדואר כיצד ניתן לעשות זאת; אך הם שלחו אותו לפקיד המכס והבלו, ששלח אותו לנציבי הביטוח, ששלחו אותו לאגודה מאושרת, אשר שלחה אותו בחילול קודש - אך לא משנה. מקורות: