קומבינטוריקה, בדיקת מקרים, תהליכים
קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.
-
חידת המאה
האם תוכלו לכתוב `100` בצורה של מספר מעורב, תוך שימוש בכל תשע הספרות פעם אחת בלבד? המתמטיקאי הצרפתי המכובד, אדוארד לוקאס, מצא שבע דרכים שונות לעשות זאת, והביע את ספקותיו לגבי קיומן של דרכים אחרות. למעשה יש בדיוק אחת-עשרה דרכים ולא יותר. הנה אחת מהן, `91 5742/638`. בתשע מהדרכים האחרות יש באופן דומה שתי ספרות בחלק השלם של המספר, אך לביטוי האחד-עשר יש רק ספרה אחת שם. האם הקורא יכול למצוא את הצורה האחרונה הזו?
מקורות:נושאים:תורת המספרים -> חשבון השאריות -> סימני חלוקה לוגיקה -> הגיון אריתמטיקה -> שברים קומבינטוריקה -> בדיקת מקרים -> תהליכים -
המאה הדיגיטלית
`1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9 = 100`.
נדרש להציב סימנים אריתמטיים בין תשע הספרות כך שהתוצאה תהיה שווה ל- `100`. כמובן, אסור לשנות את הסדר המספרי הקיים של הספרות. האם תוכלו לתת פתרון נכון המשתמש ב- (`1`) מספר הסימנים המועט ביותר האפשרי, וב- (`2`) מספר המינימלי של קווים או נקודות נפרדים של העט? כלומר, יש צורך להשתמש בכמה שפחות סימנים אפשריים, וסימנים אלה צריכים להיות בצורה הפשוטה ביותר. סימני החיבור והכפל (+ ו- ×) ייחשבו כשני קווים, סימן החיסור (-) כקו אחד, סימן החילוק (÷) כשלושה, וכן הלאה.
מקורות: -
חמשת השודדים
חמשת השודדים הספרדים, אלפונסו, בניטו, קרלוס, דייגו ואסטבן, ספרו את שללם לאחר פשיטה, כאשר התגלה שהם שדדו יחד בדיוק `200` דובלונים. אחד מהחבורה ציין שאם לאלפונסו יהיה פי שנים עשר, לבניטו פי שלושה, לקרלוס אותו סכום, לדייגו חצי מהסכום ולאסטבן שליש מהסכום, עדיין יהיו להם יחד בדיוק `200` דובלונים. כמה דובלונים היו לכל אחד?
ישנן תשובות נכונות רבות באותה מידה לשאלה זו. הנה אחת מהן:
A 6 × 12 = 72 B 12 × 3 = 36 C 17 × 1 = 17 D 120 × ½ = 60 E 45 × 1/3 = 15 200 200 החידה היא לגלות בדיוק כמה תשובות שונות יש, בהנחה שלכל אחד היה משהו ושאסור שיהיה כסף חלקי — רק דובלונים בכל מקרה.
בעיה זו, שניסוחה שונה במקצת, הוצגה על ידי טרטליה (נפטר ב-`1559`), והוא החמיא לעצמו שהוא מצא פתרון אחד; אבל מתמטיקאי צרפתי ידוע (M.A. Labosne), בעבודה מהעת האחרונה, אומר שקוראיו יופתעו כאשר הוא מבטיח להם שיש `6,639` תשובות נכונות שונות לשאלה. האם זה כך? כמה תשובות יש?
מקורות:נושאים:תורת המספרים אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים אלגברה -> משוואות -> משוואות דיופנטיות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 133
-
מטע בבורמה
לפני זמן קצר קיבלתי מכתב מעניין מהכומר הבריטי במייקטילה, בורמה העליונה, בו כתב לי הכומר שנהנה באונייה בדרכו לשם לנסות לפתור את החידה הקטנה הזו.

אם יש לו מטע של ארבעים ותשעה עצים, נטועים בצורת ריבוע כפי שמוצג באיור המצורף, הוא רוצה לדעת איך הוא יכול לכרות עשרים ושבעה מהעצים כך שעשרים ושניים העצים שיישארו יעמדו בשורות רבות ככל האפשר עם ארבעה עצים בכל שורה.
כמובן שלא יכולים להיות יותר מארבעה עצים בשורה.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 212
-
חידת מוסך המכוניות
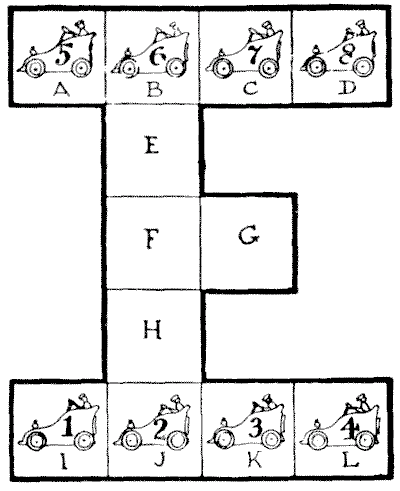
הקשיים של בעל מוסך מוסבים למעין בילוי שיש בו קסם מיוחד. כל מה שצריך זה להכין תוכנית או דיאגרמה פשוטה על דף נייר או קרטון ולמספר שמונה אסימונים, מ-`1` עד `8`. אז משפחה שלמה יכולה להיכנס לתחרות משעשעת כדי למצוא את הפתרון הטוב ביותר לקושי.
האיור מייצג את תוכנית מוסך המכוניות, עם מקום לשתים עשרה מכוניות. אבל השטח מצומצם בצורה לא נוחה, ולכן הבעלים נתקל לעתים קרובות במבוכה רבה. נניח, למשל, ששמונה המכוניות הממוספרות מ-`1` עד `8` נמצאות במקומות המוצגים, איך ניתן להזיז אותן בצורה המהירה ביותר כך ש-`1, 2, 3` ו-`4` יחליפו מקומות עם `5, 6, 7` ו-`8` — כלומר, כשהמספרים עדיין רצים משמאל לימין, כפי שהם כרגע, אבל השורה העליונה הוחלפה בשורה התחתונה? מהו המספר הקטן ביותר של מהלכים אפשריים?
מכונית אחת זזה בכל פעם, וכל מרחק נחשב למהלך אחד. כדי למנוע אי הבנות, מקומות העצירה מסומנים בריבועים, ויכולה להיות רק מכונית אחת בריבוע בכל פעם.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 224
-
חידת ההחלפה
הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—
A B C D E F G H I J K L המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?
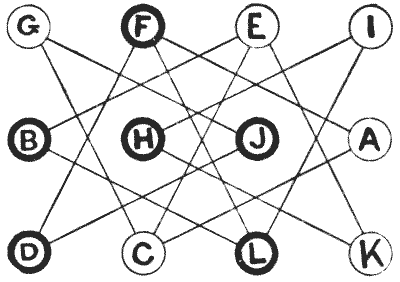
אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.
מקורות:נושאים:קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 234
-
הטיול הגדול
אחת החידות היומיומיות של החיים היא תכנון מסלולים. אם אתם יוצאים לחופשה על אופניים, או לטיול מוטורי, תמיד עולה השאלה כיצד לנצל את הזמן והמשאבים שלכם בצורה הטובה ביותר. החלטתם להגיע למקום מסוים, לכלול ביקורים בעיר כזו וכזו, לנסות לראות משהו מעניין במיוחד במקום אחר, ואולי לנסות לבקר חבר ותיק בנקודה שלא תוציא אתכם בהרבה מהדרך. אז אתם צריכים לתכנן את המסלול שלכם כדי להימנע מכבישים גרועים, אזורים לא מעניינים, ואם אפשר, מהצורך לחזור באותה דרך שבה נסעתם. עם מפה לפניכם, ניגשים לפתרון החידה המעניינת. אציג לכם שאלה קטנה המבוססת על קווים אלה.
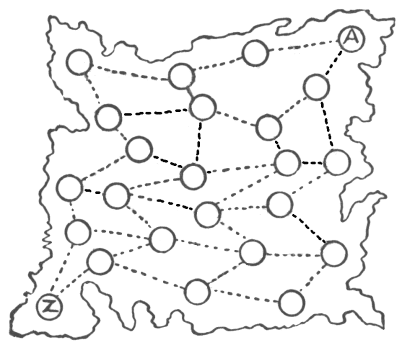
אני מציג מפה גסה של מדינה—אין צורך לומר איזו מדינה—העיגולים מייצגים ערים והקווים המקווקווים את מסילות הברזל המחברות ביניהן. עכשיו, בעיר המסומנת A חי אדם שנולד שם, ובמשך כל חייו מעולם לא עזב את מקום הולדתו. מנעוריו הוא היה חרוץ מאוד, דבק בעקביות במקצועו, ולא היה לו רצון לשוטט בחוץ. עם זאת, בהגיעו לגיל חמישים הוא החליט לראות קצת מהמדינה שלו, ובמיוחד לבקר חבר ותיק מאוד שגר בעיר המסומנת Z. מה שהוא הציע היה כזה: שהוא יתחיל מביתו, ייכנס לכל עיר פעם אחת בלבד, ויסיים את מסעו ב-Z. מכיוון שהוא החליט לבצע את הטיול הגדול הזה ברכבת בלבד, הוא התקשה קצת לתכנן את המסלול שלו, אבל בסופו של דבר הוא הצליח לעשות זאת. איך הוא הצליח? אל תשכחו שצריך לבקר בכל עיר פעם אחת, ולא יותר מפעם אחת.
 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 250
-
החידה המאולצת
בכמה דרכים שונות ניתן לקרוא את המילה DEIFIED (מאוּלָה) בסידור הזה, באותם התנאים כמו בחידה האחרונה, בתוספת שאתה יכול להשתמש בכל אות פעמיים באותו קריאה?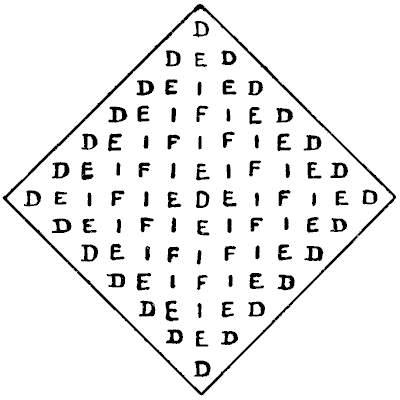 מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 257
-
החידה של חנה
איש היה מאוהב בגברת צעירה ששמה הפרטי היה חנה. כשביקש ממנה להיות אשתו היא כתבה את אותיות שמה באופן הזה:— והבטיחה שתהיה שלו אם יוכל לומר לה נכונה בכמה דרכים שונות אפשר לאיית את שמה, תמיד לעבור מאות אחת לאחרת שהיא סמוכה. צעדים אלכסוניים מותרים כאן. בין אם עשתה זאת רק כדי להקניט אותו או לבחון את חוכמתו לא נרשם, אבל משביע רצון לדעת שהוא הצליח. האם היית מצליח באותה מידה? קח את העיפרון שלך ונסה. אתה יכול להתחיל מכל אחת מהאותיות ה' וללכת אחורה או קדימה ובכל כיוון, כל עוד כל האותיות באיות סמוכות זו לזו. כמה דרכים יש, שאף שתיים מהן אינן זהות לחלוטין?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
והבטיחה שתהיה שלו אם יוכל לומר לה נכונה בכמה דרכים שונות אפשר לאיית את שמה, תמיד לעבור מאות אחת לאחרת שהיא סמוכה. צעדים אלכסוניים מותרים כאן. בין אם עשתה זאת רק כדי להקניט אותו או לבחון את חוכמתו לא נרשם, אבל משביע רצון לדעת שהוא הצליח. האם היית מצליח באותה מידה? קח את העיפרון שלך ונסה. אתה יכול להתחיל מכל אחת מהאותיות ה' וללכת אחורה או קדימה ובכל כיוון, כל עוד כל האותיות באיות סמוכות זו לזו. כמה דרכים יש, שאף שתיים מהן אינן זהות לחלוטין?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 259
-
חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים
אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 262