קומבינטוריקה, בדיקת מקרים, תהליכים

קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.

  • שאלה

    מספר N יקרא מוצלח אם הוא מקיים את שני התנאים הבאים:
    * N הוא מספר חיובי שלם שמתחלק ב-101,
    * ברישום של N מופיעות בדיוק שתי ספרות לא אפסיות.
    למשל המספר 2020 הוא מוצלח, ואילו המספר 12120 אינו מוצלח כי יש בו 4 ספרות לא אפסיות.
    מצאו את כמות המספרים המוצלחים שקטנים מ- `10^40`. מקורות:

  • חידה בהיפוכים

    רוב האנשים יודעים שאם לוקחים סכום כסף כלשהו בלירות, שילינגים ופני, שבו מספר הלירות (פחות מ-£`12`) עולה על מספר הפני, הופכים אותו (קוראים ללירות פני ולפני לירות), מוצאים את ההפרש, ואז הופכים ומוסיפים את ההפרש הזה, התוצאה היא תמיד £`12, 18`s. `11`d. אבל אם נשמיט את התנאי, "פחות מ-£`12`", וניתן לאפס לייצג שילינגים או פני—(`1`) מהו הסכום הנמוך ביותר שעליו הכלל לא יחול? (`2`) מהו הסכום הגבוה ביותר שעליו הוא יחול? כמובן, כאשר הופכים סכום כזה כמו £`14, 15`s. `3`d., ניתן לכתוב אותו £`3, 16`s. `2`d., שהוא זהה ל-£`3, 15`s. `14`d. מקורות:

  • ספרות וריבועים

    ניתן לראות בתרשים שסידרנו את תשע הספרות בריבוע כך שהמספר בשורה השנייה גדול פי שניים מהמספר בשורה הראשונה, והמספר בשורה התחתונה גדול פי שלושה מהמספר בשורה העליונה. ישנן שלוש דרכים נוספות לסדר את הספרות כך שיתקבל אותו פתרון. האם תוכלו למצוא אותן? מקורות:

  • חידת הלוקרים

     

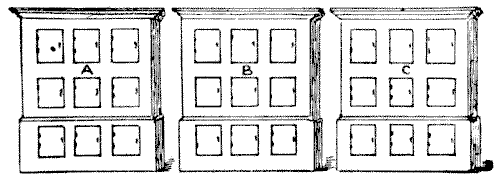
    לאיש היו במשרדו שלושה ארונות, שבכל אחד מהם תשעה לוקרים, כפי שמוצג בדיאגרמה. הוא הורה לפקיד שלו להציב ספרה שונה על כל לוקר בארון A, ולעשות את אותו הדבר בארון B ובארון C. מכיוון שמותר לנו כאן לקרוא לאפס ספרה, ולא נאסר עליו להשתמש באפס כמספר, ברור שהייתה לו האפשרות להשמיט כל אחת מעשר הספרות מכל ארון.

    כעת, המעסיק לא אמר שהלוקרים ימוספרו בסדר מספרי כלשהו, והוא הופתע לגלות, לאחר שהעבודה הסתיימה, שהספרות כנראה עורבבו באופן אקראי. כשקרא לפקיד שלו להסבר, הנער האקסצנטרי הצהיר שהעלתה בדעתו המחשבה לסדר את הספרות כך שבכל מקרה הן יצרו תרגיל חיבור פשוט, כאשר שתי השורות העליונות של הספרות יוצרות את הסכום בשורה התחתונה. אבל הנקודה המפתיעה ביותר הייתה זו: שהוא סידר אותן כך שהחיבור ב-A נתן את הסכום הקטן ביותר האפשרי, שהחיבור ב-C נתן את הסכום הגדול ביותר האפשרי, וכי כל תשע הספרות בסך הכל בשלושת הסכומים היו שונות. החידה היא להראות כיצד ניתן לעשות זאת. אין לאפשר עשרונים והאפס אינו יכול להופיע במקום המאות.

    מקורות:

  • שלוש הקבוצות

    בכתב העת "Nouvelles Annales de Mathématiques" הופיעה החידה הבאה כשינוי לאחת מ"חידות קנטרברי" שלי. סדר את תשע הספרות בשלוש קבוצות של שתיים, שלוש וארבע ספרות, כך ששני המספרים הראשונים כאשר מכפילים אותם זה בזה יוצרים את השלישי. לדוגמה, `12` × `483` = `5,796`. אני מציע כעת לכלול גם את המקרים שבהם יש ספרה אחת, ארבע וארבע ספרות, כגון `4` × `1,738` = `6,952`. האם תוכל למצוא את כל הפתרונות האפשריים בשני המקרים? מקורות:

  • תשעת האסימונים

    יש לי תשעה אסימונים, שעל כל אחד מהם רשומה אחת מתשע הספרות, `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. סידרתי אותם על השולחן בשתי קבוצות, כפי שניתן לראות באיור, כך שייצרו שני תרגילי כפל, וגיליתי ששני התרגילים נתנו את אותה מכפלה. תגלו ש-`158` כפול `23` זה `3,634`, וגם `79` כפול `46` זה `3,634`. עכשיו, החידה שאני מציע היא לסדר מחדש את האסימונים כך שנקבל את המכפלה הגדולה ביותר האפשרית. מה הדרך הטובה ביותר למקם אותם? זכרו ששתי הקבוצות חייבות להכפיל לאותה כמות, וחייבים להיות שלושה אסימונים כפול שניים במקרה אחד, ושניים כפול שני אסימונים במקרה השני, בדיוק כמו עכשיו. מקורות:

  • עשרת המונים

    במקרה זה אנו משתמשים באפס בנוסף ל-`1, 2, 3, 4, 5, 6, 7, 8, 9`. החידה היא, כבמקרה הקודם, לסדר את עשרת המונים כך שמכפלות שני הכפל יהיו זהות, ואפשר שיהיו ספרה אחת או יותר במכפיל, כרצונך. האמור לעיל הוא הישג קל מאוד; אך נדרש גם למצוא את שני הסידורים הנותנים זוגות של המכפלות הגבוהות והנמוכות ביותר האפשריות. כמובן שיש להשתמש בכל מונה, ולא ניתן למקם את הספרה אפס משמאל לשורת ספרות כאשר אין לה השפעה. שברים פשוטים או עשרוניים אינם מותרים. מקורות:

  • כפל ספרותי

    הנה בעיה משעשעת נוספת עם תשע הספרות, כאשר הספרה אפס אינה נכללת. באמצעות כל ספרה פעם אחת בלבד, אנו יכולים ליצור שני תרגילי כפל בעלי מכפלה זהה, וניתן לעשות זאת בדרכים רבות. לדוגמה, 7x658 ו-14x329 מכילים את כל הספרות פעם אחת, והמכפלה בכל מקרה זהה - `4,606`. כעת, ניתן לראות שסכום הספרות במכפלה הוא `16`, שאינו הסכום הגבוה או הנמוך ביותר שניתן להשיג. האם תוכלו למצוא את הפתרון לבעיה שנותן את הסכום הנמוך ביותר האפשרי של ספרות במכפלה המשותפת? וגם את זה שנותן את הסכום הגבוה ביותר האפשרי? מקורות:

  • החידה של פיירו

    פיירו באיור עומד בתנוחה המייצגת את סימן הכפל. הוא מצביע על העובדה המוזרה ש-`15` כפול `93` מניב בדיוק את אותן הספרות (`1,395`), אך מסודרות באופן שונה. החידה היא לקחת ארבע ספרות כלשהן שתרצו (כולן שונות) ולסדר אותן באופן דומה, כך שהמספר שנוצר מצד אחד של פיירו כאשר הוא מוכפל במספר בצד השני יפיק את אותן הספרות. ישנן דרכים מעטות מאוד לעשות זאת, ואני אתן את כל המקרים האפשריים. האם תוכלו למצוא את כולם? מותר לכם לשים שתי ספרות בכל צד של פיירו כמו בדוגמה המוצגת, או למקם ספרה בודדת בצד אחד ושלוש ספרות בצד השני. אם היינו משתמשים רק בשלוש ספרות במקום בארבע, הדרכים האפשריות היחידות הן אלה: `3` כפול `51` שווה ל-`153`, ו-`6` כפול `21` שווה ל-`126`. מקורות:

  • חידת תגי המספרים

    במקום בו מועסקים מספר רב של פועלים בבניין, נהוג לספק לכל אדם דיסקית קטנה הנושאת את מספרו. דיסקיות אלו נתלות על לוח על ידי הפועלים כשהם מגיעים, ומשמשות כמעקב אחר דייקנות. פעם שמתי לב שמנהל עבודה הסיר מספר תגים אלה מהלוח שלו והניח אותם על טבעת מפוצלת שנשא בכיסו. זה מיד נתן לי את הרעיון לחידה טובה. למעשה, אני אספר לקוראים שלי שכך בדיוק עולים רעיונות לחידות. אתה לא יכול באמת ליצור רעיון: זה קורה - ואתה צריך להיות בכוננות כדי לתפוס אותו כשזה קורה.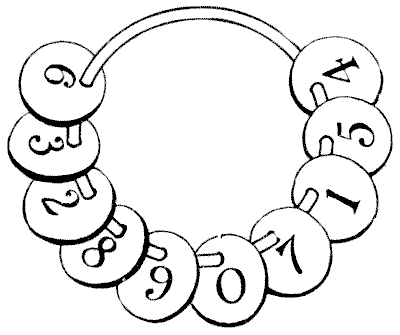 ניתן לראות מהאיור שיש עשרה תגים אלה על טבעת, ממוספרים מ-`1` עד `9` ו-`0`. החידה היא לחלק אותם לשלוש קבוצות מבלי להסיר אף אחד מהם מהטבעת, כך שהקבוצה הראשונה כפול השנייה תיתן את הקבוצה השלישית. לדוגמה, אנו יכולים לחלק אותם לשלוש קבוצות, `2`—`8` `9` `7`—`1` `5` `4` `6` `3`, על ידי הבאת ה-`6` וה-`3` סביב ל-`4`, אבל לצערי שתי הראשונות כשהן מוכפלות יחד לא יוצרות את השלישית. האם אתה יכול להפריד אותם נכון? כמובן שמותר לך שיהיו לך כמה תגים שתרצה בכל קבוצה. החידה דורשת קצת תושייה, אלא אם כן יש לך מזל לפגוע בתשובה במקרה. מקורות: