קומבינטוריקה, בדיקת מקרים, תהליכים
קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.
-
דומינו בסדרה
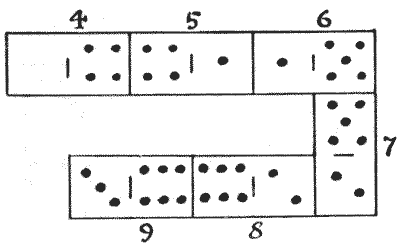 ניתן לראות ששיחקתי שישה אבני דומינו, באיור, בהתאם לכללים הרגילים של המשחק, `4` נגד `4, 1` נגד `1`, וכן הלאה, ועדיין סכום הנקודות על אבני הדומינו העוקבות, `4, 5, 6, 7, 8, 9`, נמצא בסדרה חשבונית; כלומר, למספרים שנלקחו לפי הסדר יש הפרש קבוע של `1`. בכמה דרכים שונות נוכל לשחק שישה אבני דומינו, מקופסה רגילה של עשרים ושמונה, כך שהמספרים עליהם יהיו בסדרה חשבונית? אנחנו תמיד חייבים לשחק משמאל לימין, ומספרים בסדרה חשבונית יורדת (כגון `9, 8, 7, 6, 5, 4`) אינם קבילים.
מקורות:
ניתן לראות ששיחקתי שישה אבני דומינו, באיור, בהתאם לכללים הרגילים של המשחק, `4` נגד `4, 1` נגד `1`, וכן הלאה, ועדיין סכום הנקודות על אבני הדומינו העוקבות, `4, 5, 6, 7, 8, 9`, נמצא בסדרה חשבונית; כלומר, למספרים שנלקחו לפי הסדר יש הפרש קבוע של `1`. בכמה דרכים שונות נוכל לשחק שישה אבני דומינו, מקופסה רגילה של עשרים ושמונה, כך שהמספרים עליהם יהיו בסדרה חשבונית? אנחנו תמיד חייבים לשחק משמאל לימין, ומספרים בסדרה חשבונית יורדת (כגון `9, 8, 7, 6, 5, 4`) אינם קבילים.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 378
-
חמש אבני דומינו
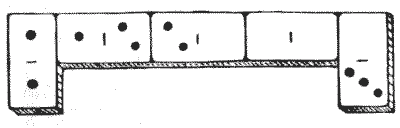
הנה חידה קטנה חדשה שאינה קשה, אך כנראה תמצא חן בעיני הקוראים שלי. ניתן לראות שחמש אבני הדומינו מסודרות ברצף נכון (כלומר, עם `1` כנגד `1, 2` כנגד `2`, וכן הלאה), כך שהמספר הכולל של הנקודות בשתי אבני הדומינו הקיצוניות הוא חמש, וסכום הנקודות בשלוש אבני הדומינו באמצע הוא גם חמש. ישנן רק שלוש סידורים אחרים שנותנים חמש עבור הסכומים. הם: —
(1—0) (0—0) (0—2) (2—1) (1—3) (4—0) (0—0) (0—2) (2—1) (1—0) (2—0) (0—0) (0—1) (1—3) (3—0) עכשיו, כמה סידורים דומים יש לחמש אבני דומינו שייתנו שש במקום חמש בשני הסכומים?
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 379
-
פאזל מסגרת הקלפים
באיור יש לנו מסגרת הבנויה מעשרה קלפי משחק, אס עד עשר יהלום. הילדים שהכינו אותה רצו שהנקודות ניקוד בכל ארבעת הצדדים יסתכמו באופן שווה, אבל הם נכשלו בניסיונם וויתרו עליה כבלתי אפשרית. ניתן לראות שהנקודות בשורה העליונה, בשורה התחתונה ובצד שמאל מסתכמות כולן ב-`14`, אבל הצד הימני מסתכם ב-`23`. עכשיו, מה שהם ניסו לעשות הוא די אפשרי. האם אתה יכול לסדר מחדש את עשרת הקלפים באותה תצורה כך שכל ארבעת הצדדים יסתכמו באופן שווה? כמובן שהם לא צריכים להסתכם ב-`14`, אלא בכל מספר שתבחר.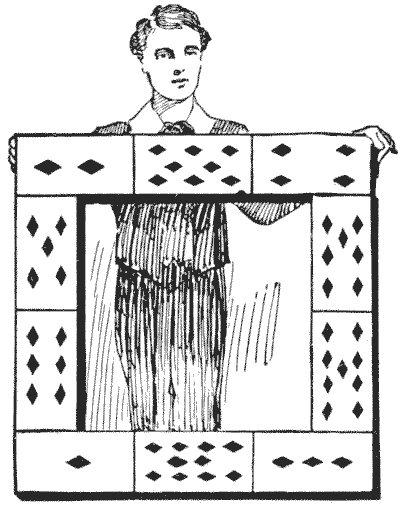 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 381
-
צלב הקלפים
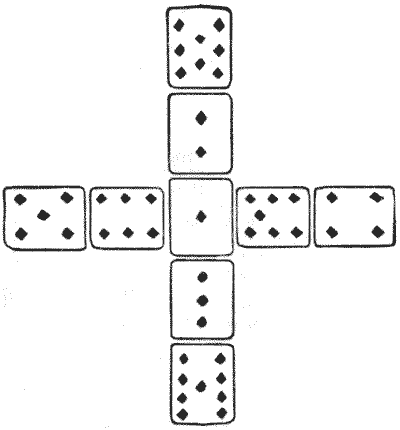 במקרה זה אנו משתמשים רק בתשעה קלפים - האס עד תשע יהלומים. החידה היא לסדר אותם בצורת צלב, בדיוק כפי שמוצג באיור, כך שהנקודות בפס האנכי ובפס האופקי יסתכמו באופן שווה. בדוגמה הנתונה, ניתן לראות ששני הכיוונים מסתכמים ל-`23`. מה שאני רוצה לדעת הוא, כמה דרכים שונות יש לסדר מחדש את הקלפים כדי להגיע לתוצאה זו? ניתן לראות כי, מבלי להשפיע על הפתרון, אנו יכולים להחליף את ה-`5` עם ה-`6`, את ה-`5` עם ה-`7`, את ה-`8` עם ה-`3`, וכן הלאה. כמו כן, אנו יכולים לגרום לפסים האופקי והאנכי להחליף מקומות. אבל מניפולציות ברורות כאלה אינן נחשבות לפתרונות שונים. כולן וריאציות בלבד של פתרון יסודי אחד. עכשיו, כמה פתרונות שונים באופן מהותי כאלה יש? הנקודות לא צריכות, כמובן, תמיד להסתכם ל-`23`.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
במקרה זה אנו משתמשים רק בתשעה קלפים - האס עד תשע יהלומים. החידה היא לסדר אותם בצורת צלב, בדיוק כפי שמוצג באיור, כך שהנקודות בפס האנכי ובפס האופקי יסתכמו באופן שווה. בדוגמה הנתונה, ניתן לראות ששני הכיוונים מסתכמים ל-`23`. מה שאני רוצה לדעת הוא, כמה דרכים שונות יש לסדר מחדש את הקלפים כדי להגיע לתוצאה זו? ניתן לראות כי, מבלי להשפיע על הפתרון, אנו יכולים להחליף את ה-`5` עם ה-`6`, את ה-`5` עם ה-`7`, את ה-`8` עם ה-`3`, וכן הלאה. כמו כן, אנו יכולים לגרום לפסים האופקי והאנכי להחליף מקומות. אבל מניפולציות ברורות כאלה אינן נחשבות לפתרונות שונים. כולן וריאציות בלבד של פתרון יסודי אחד. עכשיו, כמה פתרונות שונים באופן מהותי כאלה יש? הנקודות לא צריכות, כמובן, תמיד להסתכם ל-`23`.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 382
-
חידת קלף ה-"T"
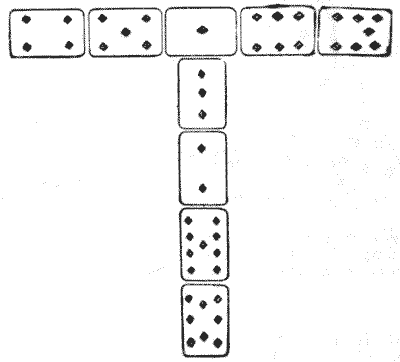 חידה משעשעת עם קלפים היא לקחת את תשעת הקלפים מסדרה אחת, מאס ועד תשע כולל, ולסדר אותם בצורת האות "T," כפי שמוצג באיור, כך שהנקודות בשורה האופקית יספרו אותו דבר כמו אלו בעמודה. בדוגמה הנתונה הם מסתכמים לעשרים ושלוש בשני הכיוונים. עכשיו, זה די קל להשיג סידור נכון יחיד. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת. למרות שהמספר גבוה, הפתרון לא באמת קשה אם נתקוף את החידה בצורה הנכונה. את הדרך ההפוכה המתקבלת על ידי שיקוף האיור במראה לא נספור כשונה, אך כל שאר השינויים במיקומים היחסיים של הקלפים ייספרו כאן. כמה דרכים שונות יש?
מקורות:
חידה משעשעת עם קלפים היא לקחת את תשעת הקלפים מסדרה אחת, מאס ועד תשע כולל, ולסדר אותם בצורת האות "T," כפי שמוצג באיור, כך שהנקודות בשורה האופקית יספרו אותו דבר כמו אלו בעמודה. בדוגמה הנתונה הם מסתכמים לעשרים ושלוש בשני הכיוונים. עכשיו, זה די קל להשיג סידור נכון יחיד. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת. למרות שהמספר גבוה, הפתרון לא באמת קשה אם נתקוף את החידה בצורה הנכונה. את הדרך ההפוכה המתקבלת על ידי שיקוף האיור במראה לא נספור כשונה, אך כל שאר השינויים במיקומים היחסיים של הקלפים ייספרו כאן. כמה דרכים שונות יש?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 383
-
משולשי קלפים
כאן עליך לבחור את תשעת הקלפים, אס עד תשע יהלומים, ולסדר אותם בצורת משולש, בדיוק כפי שמוצג באיור, כך שהנקודות יסתכמו לאותו דבר בכל שלושת הצדדים. בדוגמה הנתונה ניתן לראות שהם מסתכמים ל-`20` בכל צד, אך למספר המסוים אין חשיבות כל עוד הוא זהה בכל שלושת הצדדים. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת.
אם פשוט תסובב את הקלפים כך שאחד משני הצדדים האחרים יהיה הכי קרוב אליך, זה לא ייחשב שונה, כי הסדר יהיה זהה. כמו כן, אם תחליף את המקומות של `4, 9, 5` עם `7, 3, 8`, ובאותו הזמן תחליף את `1` ו-`6`, זה לא יהיה שונה. אבל אם רק תחליף את `1` ו-`6`, זה יהיה שונה, כי הסדר סביב המשולש אינו זהה. הסבר זה ימנע כל ספק לגבי התנאים.
מקורות: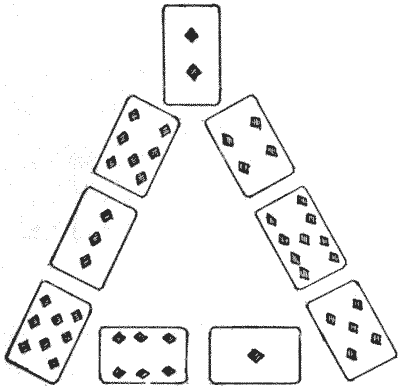
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 384
-
"STRAND" סבלנות
הרעיון לכך עלה לי כששקלתי את משחק הסבלנות שנתתי בתוך Strand Magazine לחודש דצמבר, `1910`, אשר הודפס מחדש בספרו השני של ארנסט ברגהולט Second Book of Patience Games, תחת השם החדש "המלך אלברט".
צרו שתי ערימות קלפים באופן הבא: `9` יהלום, `8` עלה, `7` יהלום, `6` עלה, `5` יהלום, `4` עלה, `3` יהלום, `2` עלה, `1` יהלום, ו-`9` תלתן, `8` תלתן, `7` תלתן, `6` תלתן, `5` תלתן, `4` תלתן, `3` תלתן, `2` תלתן, `1` תלתן, כאשר ה-`9` של יהלומים בתחתית ערימה אחת וה-`9` של תלתן בתחתית הערימה האחרת. המטרה היא להחליף את העלים עם התלתנים, כך שהיהלומים והתלתנים עדיין יהיו בסדר מספרי בערימה אחת והתלתנים והעלים בערימה השנייה. ישנם ארבעה מקומות פנויים בנוסף לשני המקומות שתפוסים על ידי הערימות, וניתן להניח כל קלף על מקום פנוי, אבל ניתן להניח קלף רק על קלף אחר בעל ערך גבוה יותר הבא אחריו — אס על שתיים, שתיים על שלוש וכן הלאה. נדרשת סבלנות כדי לגלות את הדרך הקצרה ביותר לעשות זאת. כאשר ישנם ארבעה מקומות פנויים, ניתן לערום ארבעה קלפים בשבעה מהלכים, עם שלושה מקומות בלבד ניתן לערום אותם בתשעה מהלכים, ועם שני מקומות אי אפשר לערום יותר משני קלפים. כאשר יש לך תפיסה של עובדות אלה ודומות להן, תוכל להסיר מספר קלפים בשלמותם ולרשום `7, 9`, או כל מספר המהלכים הנדרש. הקיצור ההדרגתי של המשחק הוא מרתק, והניסיונות הראשונים הם ארוכים באופן מפתיע.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 385
-
שחקני הכדורגל
"זהו משחק נפלא!" נשמע חובב נלהב קורא. "בסיום העונה שעברה, מבין שחקני הכדורגל שאני מכיר, לארבעה נשברה זרוע שמאל, לחמישה נשברה זרוע ימין, לשניים זרוע ימין הייתה בריאה, ולשלושה זרוע שמאל הייתה בריאה." האם תוכלו לגלות מההצהרה הזו מהו המספר הקטן ביותר של שחקנים שהדובר יכול היה להכיר?
כלל לא נובע מכך שהיו ארבעה עשר אנשים, מכיוון שלדוגמה, שניים מהאנשים ששברו את זרוע שמאל יכולים להיות גם שניים מאלה שהייתה להם זרוע ימין בריאה.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 389
-
משחק החלוקים
הנה משחק חידה קטן ומעניין שנהגתי לשחק עם מכר על החוף בסלוקומב-און-סי. שני שחקנים מניחים מספר אי זוגי של חלוקים, נניח חמישה עשר, ביניהם. לאחר מכן כל אחד בתורו לוקח אחד, שניים או שלושה חלוקים (כפי שהוא בוחר), והמנצח הוא זה שמקבל מספר אי זוגי. לכן, אם אתה מקבל שבע והיריב שלך שמונה, אתה מנצח. אם אתה מקבל שש והוא מקבל תשע, הוא מנצח. האם השחקן הראשון או השני אמור לנצח, וכיצד? לאחר שפתרתם את השאלה עם חמישה עשר חלוקים, נסו שוב עם, למשל, שלושה עשר. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 392
-
משחק הקוביות המונטנגרי
מסופר כי לתושבי מונטנגרו יש משחק קוביות קטן שהוא גם גאוני וגם ראוי לחקירה. שני השחקנים בוחרים תחילה שני זוגות שונים של מספרים אי-זוגיים (תמיד גבוהים מ-`3`), ואז מטילים לסירוגין שלוש קוביות. מי שמטיל ראשון את הקוביות כך שסכומן הוא אחד מהמספרים שבחר מנצח. אם שניהם מצליחים בשתי הטלות עוקבות, זה תיקו והם מנסים שוב. לדוגמה, שחקן אחד יכול לבחור `7` ו-`15` והשני `5` ו-`13`. לאחר מכן, אם השחקן הראשון מטיל כך ששלוש הקוביות מסתכמות ל-`7` או `15`, הוא מנצח, אלא אם כן השחקן השני מקבל `5` או `13` בהטלה שלו.
החידה היא לגלות אילו שני זוגות מספרים יש לבחור כדי לתת לשני השחקנים סיכוי שווה בדיוק.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 397