קומבינטוריקה, בדיקת מקרים, תהליכים

קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.

  • הצינוק הספרדי

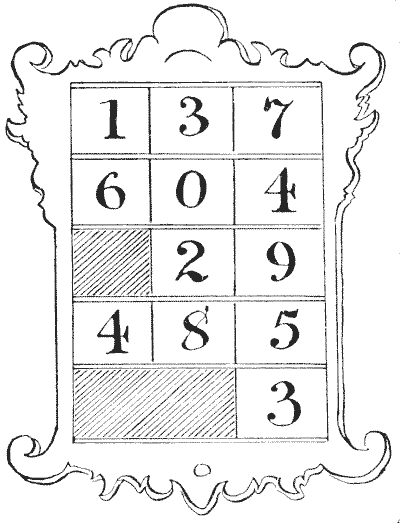
    לא רחוק מחמישים מייל מקדיז ניצב בימי הביניים מבצר, שכל עקבותיו נעלמו במשך מאות שנים. בין שאר המאפיינים המעניינים, המבצר הזה הכיל צינוק לא נעים במיוחד, המחולק לשישה עשר תאים, כולם מתקשרים זה עם זה, כפי שמוצג באיור.

    עתה, המושל היה עליז, וחובב חידות גדול. יום אחד הוא הלך לצינוק ואמר לאסירים, "בחיי!" (או המקבילה שלו בספרדית) "כולכם תשוחררו אם תוכלו לפתור את החידה הזו. עליכם לסדר את עצמכם בשישה עשר התאים כך שהמספרים על גבכם יהוו ריבוע קסם שבו כל טור, כל שורה וכל אחד משני האלכסונים יסתכמו לאותו מספר. רק זכרו זאת: שאף אחד מכם לא יהיה ביחד באותו תא."

    אחד האסירים, לאחר שעבד על הבעיה במשך יומיים או שלושה, עם חתיכת גיר, לקח על עצמו להשיג את חירותו וחירות חבריו האסירים אם הם ילכו בעקבות הוראותיו ויעברו דרך הפתח מתא לתא בסדר שבו יקרא את המספרים שלהם. 

     

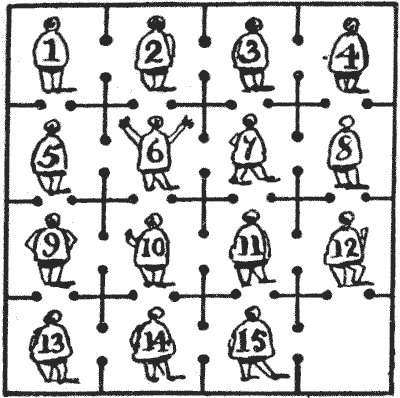
    הוא הצליח בניסיונו, ומה שמרשים יותר, כך נראה מהתיאור של שיטתו שנרשם בכתב היד העתיק שלפניי, שהוא עשה זאת במספר המהלכים המועט ביותר האפשרי. הקורא מתבקש להראות מה היו המהלכים האלה.

    מקורות:

  • הצינוקים הסיביריים

     

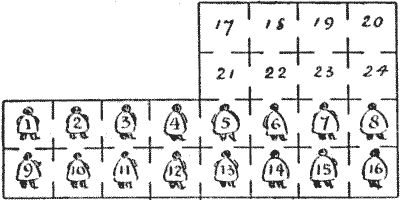
    למעלה מוצגת תוכנית מהימנה של בית כלא רוסי מסוים בסיביר. כל התאים ממוספרים, והאסירים ממוספרים במספרים זהים לתאים בהם הם נמצאים. תזונת הכלא כל כך משמינה שאסירים פוליטיים אלה חוששים תמידית שאם יגיע חנינה, הם לא יוכלו לדחוס את עצמם דרך הפתחים הצרים ולצאת. וכמובן שזה יהיה לא סביר לבקש מכל ממשלה להפיל את חומות הכלא רק כדי לשחרר את האסירים, יהיו אשר יהיו חפים מפשע. לכן אנשים אלה עושים את כל הפעילות הגופנית הבריאה שהם יכולים כדי לעכב את ההשמנה הגוברת שלהם, ואחד הבילויים שלהם ישמש אותנו כדי לספק את החידה הבאה.

    הראו, במספר המהלכים המועט ביותר האפשרי, כיצד ששת-עשר האסירים יכולים לסדר את עצמם בריבוע קסם, כך שהמספרים על גבם יסתכמו לאותו סכום בכל אחד מארבעת הטורים, ארבע השורות ושני האלכסונים, מבלי ששני אסירים היו אי פעם באותו תא יחד. מוטב שאומר, לידיעת אלה שעדיין לא הכירו את המקומות האלה, שאחת המוזרויות של בתי הכלא היא שלא מורשים לצאת מגבולות החומות שלהם. כל אסיר רשאי ללכת כל מרחק אפשרי במהלך בודד.

    מקורות:

  • טבעות הברזל המייגעות

     

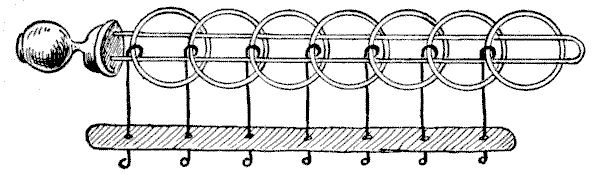
    האיור מייצג אחד מהחידות המכאניות העתיקות ביותר. מקורו אינו ידוע. קרדנו, המתמטיקאי, כתב עליו בשנת `1550`, וואליס בשנת `1693`; בעוד שאומרים שהוא עדיין נמצא בכפרים אנגליים נידחים (לפעמים מונח במקומות מוזרים, כמו מגדל פעמונים של כנסייה), עשוי מברזל, ונקרא באופן הולם "טבעות מייגעות", ומשמש את הנורווגים כיום כמנעול לקופסאות ותיקים. בחנויות הצעצועים הוא נקרא לפעמים "טבעות סיניות", אם כי נראה שאין סמכות לתיאור, ולרוב הוא מכונה בשם הלא מספק "הטבעות המבלבלות". הצרפתים קוראים לזה "Baguenaudier."

    ניתן לראות שהחידה מורכבת מ-לולאה פשוטה של חוט המקובעת בידית שאותה מחזיקים ביד שמאל, וממספר מסוים של טבעות המאובטחות על ידי חוטים העוברים דרך חורים ב-מוט ונשמרים שם על ידי קצותיהם הקהים. החוטים פועלים בחופשיות במוט, אך אינם יכולים להיפרד ממנו, וגם לא ניתן להסיר את החוטים מהטבעות. החידה הכללית היא לנתק את הלולאה לחלוטין מכל הטבעות, ואז להחזיר את כולן שוב.

    כעת, ניתן לראות במבט חטוף שניתן להסיר את הטבעת הראשונה (מימין) בכל עת על ידי החלקתה מעל הקצה והשלכתה דרך הלולאה; או שאפשר להחזיר אותה על ידי היפוך הפעולה. מלבד זאת, הטבעת היחידה שניתן להסיר אי פעם היא זו שבמקרה נמצאת השנייה הסמוכה על הלולאה בקצה הימני. כך, כשכל הטבעות עליה, ניתן להפיל את השנייה מיד; כשהטבעת הראשונה למטה, אינך יכול להפיל את השנייה, אך תוכל להסיר את השלישית; כששלוש הטבעות הראשונות למטה, אינך יכול להפיל את הרביעית, אך תוכל להסיר את החמישית; וכן הלאה. יתברר שאפשר להפיל את הטבעות הראשונה והשנייה יחד או להחזיר אותן יחד; אך כדי למנוע בלבול, לא נאפשר את המהלך הכפול החריג הזה, ונגיד שניתן להחזיר או להסיר רק טבעת אחת בכל פעם.

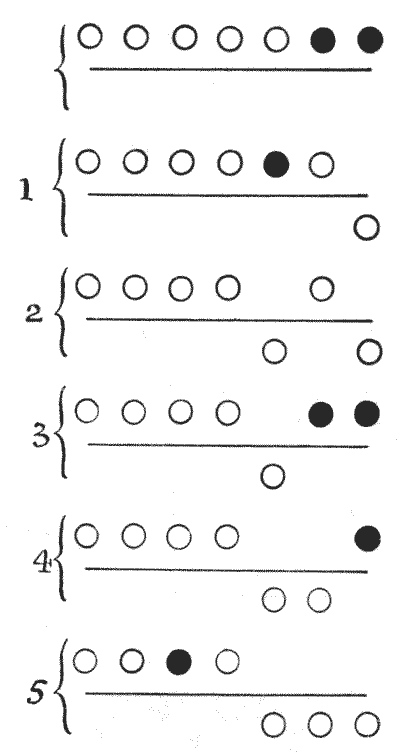
    אנו יכולים להסיר טבעת אחת ב-`1` מהלך; שתי טבעות ב-`2` מהלכים; שלוש טבעות ב-`5` מהלכים; ארבע טבעות ב-`10` מהלכים; חמש טבעות ב-`21` מהלכים; ואם נמשיך להכפיל (ולהוסיף אחד כאשר מספר הטבעות הוא אי-זוגי) נוכל לברר בקלות את מספר המהלכים להסרת כל מספר טבעות לחלוטין. כדי להוריד את כל שבע הטבעות נדרשים `85` מהלכים. בואו נסתכל על חמשת המהלכים שנעשו בהסרת שלוש הטבעות הראשונות, העיגולים מעל הקו מייצגים טבעות על הלולאה ואלה שמתחת מייצגים טבעות מחוץ ללולאה.

    הפילו את הטבעת הראשונה; הפילו את השלישית; הרימו את הראשונה; הפילו את השנייה; והפילו את הראשונה—`5` מהלכים, כפי שמוצג בבירור בתרשימים. העיגולים הכהים מראים בכל שלב, ממצב ההתחלה ועד הסיום, אילו טבעות אפשר להפיל. לאחר מהלך `2` יורגש שלא ניתן להפיל אף טבעת עד שאחת תוחזר, מכיוון שהטבעות הראשונה והשנייה מימין שנמצאות כעת על הלולאה אינן יחד. לאחר המהלך החמישי, אם ברצוננו להסיר את כל שבע הטבעות, עלינו כעת להפיל את החמישית. אבל לפני שנוכל להסיר אז את הרביעית, יש צורך להחזיר את שלוש הראשונות ולהסיר את שתי הראשונות. אז יהיו לנו `7, 6, 4, 3` על הלולאה, ולכן נוכל להפיל את הרביעית. כשנחזיר `2` ו-`1` ונסיר `3, 2, 1`, נוכל להפיל את הטבעת השביעית. הפעולה הבאה אז תהיה להשיג `6, 5, 4, 3, 2, 1` על הלולאה ולהסיר `4, 3, 2, 1`, ואז `6` תרד; ואז להשיג `5, 4, 3, 2, 1` על הלולאה, ולהסיר `3, 2, 1`, ואז `5` תרד; ואז להשיג `4, 3, 2, 1` על הלולאה ולהסיר `2, 1`, ואז `4` תרד; ואז להשיג `3, 2, 1` על הלולאה ולהסיר `1`, ואז `3` תרד; ואז להשיג `2, 1` על הלולאה, ואז `2` תרד; ו-`1` תיפול דרך במהלך ה-85, ותשאיר את הלולאה חופשית לחלוטין. על הקורא להיות מסוגל כעת להבין את החידה, בין אם יש לו אותה ביד בצורה מעשית ובין אם לא.

     

    הבעיה המסוימת שאני מציע היא פשוט זו. נניח שיש בסך הכל ארבע עשרה טבעות על טבעות הברזל המייגעות, ואנו ממשיכים להסיר את כולן בצורה הנכונה כדי לא לבזבז אף מהלך. מה יהיה מצב הטבעות לאחר שבוצע המהלך ה-`9`,999?

    מקורות:

  • הבעיה של לוח מזמורי התפילה

    ויקאר צ'אמפלי סנט וויניפרד הנכבד נמצא במצוקה רבה. קושי כנסייתי קטן התעורר, ונראה שכל האינטליגנציה המשולבת של הקהילה אינה מסוגלת להתגבר עליו. מה הקושי הזה, אספר בהמשך, אך ייתכן שיוסיף לעניין בבעיה אם אתן תחילה תיאור קצר של המצב המוזר שנוצר. הכל קשור ללוחות מזמורי התפילה של הכנסייה, שהלוחות שלהם ניזוקו כל כך שהם חדלו למלא את המטרה שלשמה הם נועדו. אחד מבני הקהילה הנדיבים הבטיח לשלם עבור סט לוחות חדש בתעריף עלות מסוים; אך מוזר ככל שזה יישמע, לא ניתן להגיע להסכמה לגבי מה צריכה להיות העלות הזו. יצרן הלוחות המוצע נקב במחיר שהתורם מכריז עליו כאבסורדי. הכומר הטוב חושב ששניהם טועים, אז הוא מבקש ממנהל בית הספר לפתור את התרגיל הקטן. אבל האינדיבידואל הזה מצהיר שהוא לא יכול למצוא שום כלל הנוגע לנושא הזה באף אחד מספרי החשבון שלו. לאחר שהוגשה בקשה לרופא המקומי, כאדם בעל אינטלקט ממוצע ומעלה בצ'אמפלי, הוא הבטיח לכומר שהפרקטיקה שלו כה כבדה שאין לו זמן אפילו להסתכל על כך, אם כי עוזרו לוחש שהרופא יושב ער בצורה יוצאת דופן במשך כמה לילות האחרונים. לאלמנה וילסון יש בן חכם, ששמועה אומרת שזכה פעם בפרס על פתרון חידות. הוא טוען מכיוון שהוא לא יכול למצוא שום פתרון לבעיה, זה חייב להיות קשור לריבוע המעגל, הכפלת הקוביה או חלוקת זווית לשלושה; בכל אופן, הוא מעולם לא ראה בעבר חידה על העיקרון, והוא מוותר.

     

    זה היה מצב העניינים כאשר עוזר הכומר (ש, אני חייב לומר, הודה בכנות מההתחלה שמחקר מעמיק בתאולוגיה הוציא מראשו את כל הידע במתמטיקה שהיה לו אי פעם) שלח לי בחביבות את החידה.

    לכנסייה יש שלושה לוחות מזמורים, כל אחד כדי לציין את המספרים של חמישה מזמורים שונים שיש לשיר בתפילה. כל הלוחות נמצאים בשימוש באותה תפילה. ספר המזמורים מכיל `700` מזמורים. נדרש סט מספרים חדש, ואחד מבני הקהילה מציע להגיש סט צבוע על לוחות מתכת, אך מתנה שיירכשו רק המספר הקטן ביותר של לוחות הכרחיים. עלות כל לוח היא `6`d., ועבור צביעת כל לוח החיובים הם: עבור לוח אחד, `1`s.; עבור שני לוחות דומים, `11`¾d. כל אחד; עבור שלושה לוחות דומים, `11`½d. כל אחד, וכן הלאה, כאשר התשלום הוא פרוטה אחת פחות ללוח עבור כל לוח צבוע באופן דומה. עכשיו, מה צריכה להיות העלות הנמוכה ביותר?

    הקוראים ישימו לב שעליהם להשתמש בכל שיטה לגיטימית ומעשית של חיסכון. האיור יבהיר את אופיים של שלושת לוחות המזמורים והלוחות. חמשת המזמורים מצוינים כאן באמצעות שנים עשר לוחות. לוחות אלה מחליקים בנפרד מאחור, ובאיור יש מקום, כמובן, לשלושה לוחות נוספים.

    מקורות:

  • הגנן והטבחית

    כתב לי כתב שכינה את עצמו "סיימון הפשוט", והציע שאציג חידת תחבולה מיוחדת בגיליון של השבועון ליום השוטים הבינלאומי, `1900`. אז נתתי את החידה הבאה, והיא גרמה לשעשוע רב; מתוך קהל מתחרים גדול מאוד, רבים מהם מומחים למדי, אף אדם לא פתר אותה, למרות שהיא רצה כמעט חודש.

     

    "האיור הוא סקיצה דמיונית של הכתב שלי, 'סיימון הפשוט,' מנסה לפתור את החידה האריתמטית הקטנה והתמימה הבאה. מרוץ בין גבר לאישה שהייתי עד לו באחד מיום השוטים הבינלאומי נחקק בזיכרוני. זה קרה באחוזה כפרית, שם הגנן והטבחית החליטו לרוץ לתחרות לנקודה במרחק של `100` רגל ישר וחזרה. גיליתי שהגנן רץ `3` רגל בכל צעד והטבחית רק `2` רגל, אבל אז היא עשתה שלושה צעדים לשני הצעדים שלו. עכשיו, מה הייתה תוצאת המירוץ?"

    שבועיים לאחר הפרסום הוספתי את ההערה הבאה: "הועלתה ההצעה שאולי יש תחבולה ב'חזרה', אבל אין כזו. המירוץ הוא לנקודה במרחק `100` רגל וחזרה הביתה—כלומר, מרחק של `200` רגל. כתב אחד שואל האם לוקח להם בדיוק אותו זמן להסתובב, ואני משיב שכן. נראה שאחר חושד שזה בעצם חידה, והתשובה היא ש'תוצאת המירוץ הייתה תיקו (נישואין)'. אבל לא הייתה לי כוונה כזו. החידה היא אריתמטית, כפי שהיא מתיימרת להיות."

    מקורות:

  • שאלה

    במישור מצוירים מספר ישרים ומעגלים. הוכיחו שניתן לצבוע את האזורים שאליהם חולק המישור בשני צבעים כך שאזורים שכנים (כאלה שיש להם קטע או קשת משותפים) יהיו צבועים בצבעים שונים.

  • חידת החגב

    הועלתה סברה שהחידה הזו הייתה חביבה מאוד על החניכים הצעירים של הסיטי של לונדון במאות השש-עשרה והשבע-עשרה. הקוראים בוודאי הבחינו בחגב הפליז המוזר בבורסה המלכותית. יצור ארוך שנים זה ניצל משריפות `1666` ו-`1838`. החגב, כדרכו, היה סמל של סר תומס גרשם, סוחר מכולת, שמת בשנת `1579`, ומסיבה זו הוא שימש כסמל על ידי מכולת באופן כללי. למרבה הצער עבור האגדה לגבי מקורה, החידה הופקה על ידי עצמי רק בשנת `1900`. על שנים עשר מתוך שלושה עשר הדיסקים השחורים מונחים אסימונים ממוספרים או חגבים. החידה היא להפוך את סדרם, כך שיקראו, `1, 2, 3, 4` וכו', בכיוון ההפוך, כאשר הדיסק הריק נשאר באותו מיקום כמו עכשיו. הזיזו אחד בכל פעם בכל סדר, או לדיסק הריק הסמוך או על ידי קפיצה מעל חגב אחד, כמו המהלכים בדמקה. ניתן לבצע את המהלכים או הקפיצות בכל כיוון שאפשרי בכל עת. מהם מספר המהלכים המועט ביותר שבו ניתן לעשות זאת?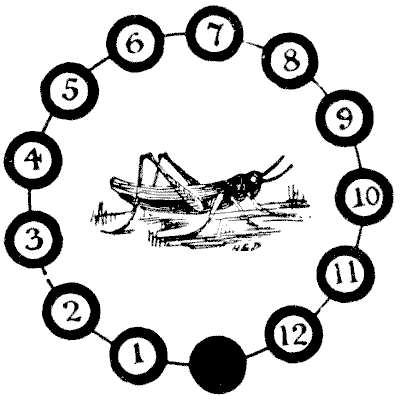 מקורות:

  • חידת מדידה חדשה

    הנה חידה חדשה במדידת נוזלים שתימצא מעניינת. לאיש יש שני כלים של עשרה ליטר מלאים ביין, וכלי מדידה של חמישה ליטר ושל ארבעה ליטר. הוא רוצה לשים בדיוק שלושה ליטרים בכל אחד משני כלי המדידה. איך הוא יעשה זאת? וכמה פעולות (מזיגות מכלי אחד לכלי שני) נדרשות? כמובן, בזבוז יין, הטיה וטריקים אחרים אסורים. מקורות: