קומבינטוריקה, בדיקת מקרים, תהליכים
קטגוריה זו מכסה בעיות הכוללות רצפים של פעולות או צעדים המתפתחים לאורך זמן או איטרציות. שאלות עשויות לשאול על תוצאת תהליך, האם הוא מסתיים, או תכונות של מצבו לאחר מספר מסוים של צעדים. קשור לעיתים קרובות לאלגוריתמים או אינווריאנטים.
-
אבירי המלך ארתור
המלך ארתור ישב ליד השולחן העגול בשלושה ערבים רצופים עם אביריו - בלובוס, קרדוק, דריאם, אריק, פלול וגלהאד - אך בשום מקרה לא היה לאף אדם כשכן מישהו שישב לידו בעבר. בערב הראשון הם ישבו בסדר אלפביתי סביב השולחן. אבל אחר כך המלך ארתור סידר את שתי הישיבות הבאות כך שבלובוס יהיה קרוב אליו ככל האפשר וגלהאד רחוק ממנו ככל האפשר. איך הוא הושיב את האבירים בצורה הטובה ביותר, תוך שהוא זוכר את הכלל שאף אביר לא יכול לקבל את אותו שכן פעמיים?מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 263
-
הכובעים הלא נכונים
"אחד הדברים המבלבלים ביותר שנתקלתי בהם לאחרונה," אמר מר ווילסון, "הוא זה. שמונה גברים סעדו בחוכמה פחותה מדי במסעדה לונדונית מסוימת. הם היו האחרונים לעזוב, אך אף גבר לא היה במצב לזהות את הכובע שלו. עכשיו, בהתחשב בכך שהם לקחו את הכובעים שלהם באופן אקראי, מה הסיכויים שכל גבר לקח כובע שלא היה שייך לו?"
"הדבר הראשון," אמר מר ווטרסון, "הוא לראות בכמה דרכים שונות ניתן לקחת את שמונת הכובעים."
"זה די קל," הסביר מר סטאבס. "כפלו יחד את המספרים, `1, 2, 3, 4, 5, 6, 7`, ו-`8`. תן לי לראות—חצי דקה—כן; יש `40,320` דרכים שונות."
"עכשיו כל מה שאתה צריך לעשות זה לראות בכמה מהמקרים האלה לאף אחד אין את הכובע שלו," אמר מר ווטרסון."
תודה, אני לא לוקח כלום," אמר מר פקהרסט. "אני לא מקנא באיש שמנסה לבצע את המשימה של כתיבת כל ארבעים אלף המקרים המוזרים האלה ואז לבחור את אלה שהוא רוצה."
כולם הסכימו שהחיים לא מספיק ארוכים בשביל סוג כזה של שעשוע; ומכיוון שאף אחד לא ראה דרך אחרת להגיע לתשובה, העניין נדחה לזמן בלתי מוגבל. האם אתה יכול לפתור את החידה?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 267
-
פאזל מלכודת העכברים
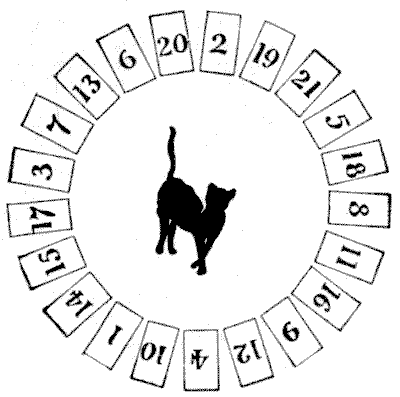 זוהי גרסה מודרנית, עם שינוי, של פאזל ישן בעל אותו השם. מספרו עשרים ואחד כרטיסים, `1, 2, 3` וכו', עד `21`, והניחו אותם במעגל בסדר המסוים המוצג באיור. כרטיסים אלה מייצגים עכברים. אתם מתחילים מכל כרטיס, קוראים לכרטיס הזה "אחד", וסופרים, "אחד, שתיים, שלוש" וכו', בכיוון השעון, וכאשר הספירה שלכם תואמת למספר על הכרטיס, ביצעתם "תפיסה", ואתם מסירים את הכרטיס. לאחר מכן התחילו בכרטיס הבא, קראו לו "אחד", ונסו שוב לבצע "תפיסה" נוספת. וכך הלאה. נניח שאתם מתחילים ב-`18`, וקוראים לכרטיס הזה "אחד", ה"תפיסה" הראשונה שלכם תהיה `19`. הסירו את `19` וה"תפיסה" הבאה שלכם היא `10`. הסירו את `10` וה"תפיסה" הבאה שלכם היא `1`. הסירו את `1`, ואם תספרו עד `21` (אסור לכם לחרוג), לא תוכלו לבצע "תפיסה" נוספת. כעת, האידיאל הוא "לתפוס" את כל עשרים ואחד העכברים, אך זה לא אפשרי כאן, ואם זה היה אפשרי, זה היה דורש רק עשרים ואחד ניסיונות שונים, לכל היותר, כדי להצליח. אבל הקורא רשאי להחליף בין שני כרטיסים לפני שהוא מתחיל. כך, אתם יכולים להחליף את ה-`6` עם ה-`2`, או את ה-`7` עם ה-`11`, או כל זוג אחר. ניתן לעשות זאת בכמה דרכים כדי לאפשר לכם "לתפוס" את כל עשרים ואחד העכברים, אם אז תתחילו במקום הנכון. לעולם אסור לכם לעבור על פני "תפיסה"; אתם תמיד חייבים להסיר את הכרטיס ולהתחיל מחדש.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
זוהי גרסה מודרנית, עם שינוי, של פאזל ישן בעל אותו השם. מספרו עשרים ואחד כרטיסים, `1, 2, 3` וכו', עד `21`, והניחו אותם במעגל בסדר המסוים המוצג באיור. כרטיסים אלה מייצגים עכברים. אתם מתחילים מכל כרטיס, קוראים לכרטיס הזה "אחד", וסופרים, "אחד, שתיים, שלוש" וכו', בכיוון השעון, וכאשר הספירה שלכם תואמת למספר על הכרטיס, ביצעתם "תפיסה", ואתם מסירים את הכרטיס. לאחר מכן התחילו בכרטיס הבא, קראו לו "אחד", ונסו שוב לבצע "תפיסה" נוספת. וכך הלאה. נניח שאתם מתחילים ב-`18`, וקוראים לכרטיס הזה "אחד", ה"תפיסה" הראשונה שלכם תהיה `19`. הסירו את `19` וה"תפיסה" הבאה שלכם היא `10`. הסירו את `10` וה"תפיסה" הבאה שלכם היא `1`. הסירו את `1`, ואם תספרו עד `21` (אסור לכם לחרוג), לא תוכלו לבצע "תפיסה" נוספת. כעת, האידיאל הוא "לתפוס" את כל עשרים ואחד העכברים, אך זה לא אפשרי כאן, ואם זה היה אפשרי, זה היה דורש רק עשרים ואחד ניסיונות שונים, לכל היותר, כדי להצליח. אבל הקורא רשאי להחליף בין שני כרטיסים לפני שהוא מתחיל. כך, אתם יכולים להחליף את ה-`6` עם ה-`2`, או את ה-`7` עם ה-`11`, או כל זוג אחר. ניתן לעשות זאת בכמה דרכים כדי לאפשר לכם "לתפוס" את כל עשרים ואחד העכברים, אם אז תתחילו במקום הנכון. לעולם אסור לכם לעבור על פני "תפיסה"; אתם תמיד חייבים להסיר את הכרטיס ולהתחיל מחדש.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 274
-
שמונה וילות
באחד מפרבריה החיצוניים של לונדון היה לאיש חלקה מרובעת שעליה החליט לבנות שמונה וילות, כפי שמוצג באיור, עם שטח משחקים משותף באמצע. לאחר שהבתים הושלמו, וכולם או חלקם הושכרו, הוא גילה שמספר הדיירים בשלושת הבתים המרכיבים צד של הריבוע היה בכל מקרה תשעה. הוא לא ציין כיצד הדיירים התפלגו, אבל הראיתי במספרים בצדי הבתים דרך אחת שבה זה יכול היה לקרות. החידה היא לגלות את המספר הכולל של הדרכים שבהן כל הבתים או חלקם יכולים להיות מאוכלסים, כך שיהיו תשעה אנשים בכל צד. כדי שלא יהיו אי הבנות, אסביר שלמרות ש-B הוא מה שאנו מכנים שיקוף של A, אלה ייחשבו כשני הסדרים שונים, בעוד ש-C, אם הוא מסתובב, ייתן ארבעה הסדרים; ואם מסתובבים מול מראה, ארבעה הסדרים אחרים. יש לספור את כל שמונתם. מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 276
-
צלבים של מוֹנִים
כל מה שאנחנו צריכים לפאזל הזה הם תשעה מוֹנִים, ממוספרים `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. ניתן לראות באיור A שהם מסודרים כך שיוצרים צלב יווני, ואילו במקרה של B הם יוצרים צלב לטיני. בשני המקרים הקורא יגלה שסכום המספרים באנך של הצלב זהה לסכום המספרים בזרוע האופקית. קל למדי להגיע לסידור כזה בניסוי וטעייה, אך הבעיה היא לגלות בדיוק בכמה דרכים שונות ניתן לעשות זאת בכל מקרה. זכרו שהיפוכים ושיקופים אינם נחשבים כשונים. כלומר, אם תסובבו את הדף הזה תקבלו ארבעה סידורים של הצלב היווני, ואם תסובבו אותו שוב מול מראה תקבלו ארבעה נוספים. אבל את שמונתם אלה מחשיבים כזהים. עכשיו, כמה דרכים שונות יש בכל מקרה?
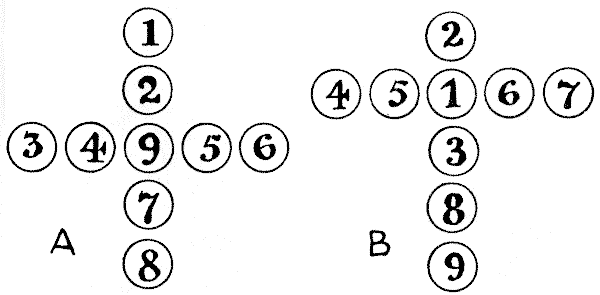 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 277
-
בניית הטטרהדרון
יש לי טטרהדרון, או פירמידה משולשת, העשויה משישה מקלות המודבקים זה לזה, כפי שמוצג באיור. האם תוכלו לספור נכונה את מספר הדרכים השונות שבהן ניתן היה להדביק את ששת המקלות הללו יחד כדי ליצור את הפירמידה?
כמה חברים עבדו על זה יחד בערב אחד, כאשר כל אדם מצטייד בשישה גפרורים כדי לעזור למחשבותיו; אבל התברר שאף שתי תוצאות לא היו זהות. אתם רואים, אם נסיר אחד מהמקלות ונסובב אותו לצד השני, זו תהיה פירמידה שונה. אם נחליף בין שניים מהמקלות התוצאה שוב תהיה שונה. אבל זכרו שניתן להעמיד כל פירמידה על כל אחד מארבעת צדדיה מבלי להיות פירמידה שונה. כמה דרכים יש בסך הכל?
מקורות: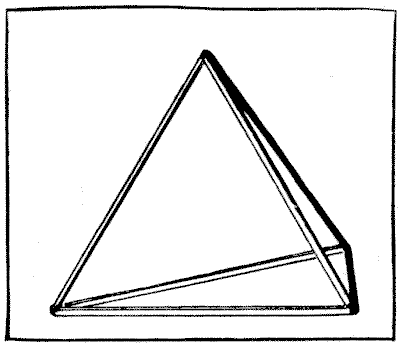
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 280
-
צביעת פירמידה
חידה זו עוסקת בצביעת ארבעת צדדיו של טטרהדרון, או פירמידה משולשת. אם תגזרו חתיכת קרטון בצורה משולשת כפי שמוצג באיור `1`, ואז תחצו אותה לאורך הקווים המקווקווים, היא תתקפל ותצור פירמידה משולשת מושלמת. ברצוני להזכיר לקוראיי שצבעי היסוד של הספקטרום הסולארי הם שבעה - סגול, אינדיגו, כחול, ירוק, צהוב, כתום ואדום. כשהייתי ילד לימדו אותי לזכור אותם באמצעות המילה המגושמת שנוצרה על ידי ראשי התיבות של הצבעים, "Vibgyor".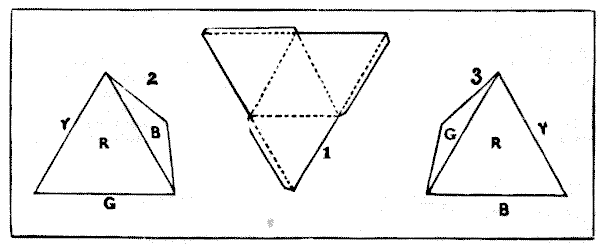 בכמה דרכים שונות ניתן לצבוע את הפירמידה המשולשת, תוך שימוש בכל מקרה בצבע אחד, שניים, שלושה או ארבעה מצבעי הספקטרום הסולארי? כמובן שצד יכול לקבל רק צבע בודד, ואף צד לא יכול להישאר לא צבוע. אבל יש נקודה אחת שאני חייב להבהיר. אין לראות בארבעת הצדדים כנפרדים מבחינה אינדיבידואלית. כלומר, אם תצבעו את הפירמידה שלכם כפי שמוצג באיור `2` (כאשר הצד התחתון ירוק והצד השני שאינו נראה הוא צהוב), ואז תצבעו אחרת בסדר המוצג באיור `3`, אלה באמת אותו הדבר ונספרים כדרך אחת. כי אם תטו את מס' `2` ימינה, הוא ייפול כך שייצג את מס' `3`. הימנעות מחזרות מסוג זה היא החידה האמיתית של העניין. אם לא ניתן למקם פירמידה צבעונית כך שתדמה בדיוק בצבעיה ובסדר היחסי שלהם לפירמידה אחרת, אז הן שונות. זכרו שדרך אחת תהיה לצבוע את כל ארבעת הצדדים באדום, אחרת לצבוע שני צדדים בירוק, ואת הצדדים הנותרים בצהוב וכחול; וכן הלאה.
מקורות:
בכמה דרכים שונות ניתן לצבוע את הפירמידה המשולשת, תוך שימוש בכל מקרה בצבע אחד, שניים, שלושה או ארבעה מצבעי הספקטרום הסולארי? כמובן שצד יכול לקבל רק צבע בודד, ואף צד לא יכול להישאר לא צבוע. אבל יש נקודה אחת שאני חייב להבהיר. אין לראות בארבעת הצדדים כנפרדים מבחינה אינדיבידואלית. כלומר, אם תצבעו את הפירמידה שלכם כפי שמוצג באיור `2` (כאשר הצד התחתון ירוק והצד השני שאינו נראה הוא צהוב), ואז תצבעו אחרת בסדר המוצג באיור `3`, אלה באמת אותו הדבר ונספרים כדרך אחת. כי אם תטו את מס' `2` ימינה, הוא ייפול כך שייצג את מס' `3`. הימנעות מחזרות מסוג זה היא החידה האמיתית של העניין. אם לא ניתן למקם פירמידה צבעונית כך שתדמה בדיוק בצבעיה ובסדר היחסי שלהם לפירמידה אחרת, אז הן שונות. זכרו שדרך אחת תהיה לצבוע את כל ארבעת הצדדים באדום, אחרת לצבוע שני צדדים בירוק, ואת הצדדים הנותרים בצהוב וכחול; וכן הלאה.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 281
-
השרשרת של חוקר העתיקות
לחוקר עתיקות הייתה כמות של חוליות עתיקות מוזרות, אותן לקח לנפח, וביקש ממנו לחבר אותן יחד ליצירת שרשרת ישרה אחת, בתנאי היחיד ששתי החוליות העגולות לא יהיו יחד. האיור הבא מציג את מראה השרשרת ואת צורתה של כל חוליה. כעת, נניח שהבעלים יפריד שוב את החוליות, ואז ייקח אותן לנפח אחר ויחזור בדיוק על ההוראות הקודמות שלו, מה הסיכויים שהחוליות לא יורכבו בדיוק כפי שהורכבו על ידי הנפח הראשון? זכרו שכל חוליה עוקבת יכולה להיות מחוברת לאחרת באחת משתי דרכים, בדיוק כפי שאתם יכולים לשים טבעת על האצבע שלכם בשתי דרכים, או לחבר את האצבעות המורות והאגודלים שלכם בשתי דרכים.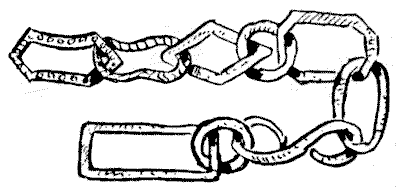 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 282
-
חֲמֵשׁ עֶשְׂרֵה אֲבָנֵי דּוֹמִינוֹ
במקרה זה, איננו משתמשים בערכה השלמה של עשרים ושמונה אבני דומינו המצויות בקופסה רגילה. אנו מוותרים על כל אבני הדומינו שיש עליהן חמש או שש ומגבילים את עצמנו לחמש-עשרה הנותרות, כאשר ארבע-כפול-ארבע היא הגבוהה ביותר.
בכמה דרכים שונות ניתן לסדר את חמש-עשרה אבני הדומינו בקו ישר בהתאם לכלל הפשוט של המשחק, שלפיו יש להניח תמיד מספר מול מספר דומה – כלומר, ארבע מול ארבע, ריק מול ריק, וכן הלאה? משמאל לימין ומימין לשמאל של אותו סידור ייחשבו כשתי דרכים שונות.
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 283
-
מטרת הצלב
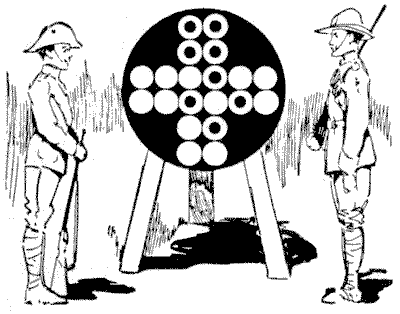 באיור יש לנו מטרה מעט מוזרה שעוצבה על ידי צלף אקסצנטרי. הרעיון שלו היה שכדי לצבור ניקוד, עליך לפגוע בארבעה עיגולים בארבע יריות כך שאותן ארבע יריות ייצרו ריבוע. ניתן לראות מהתוצאות שנרשמו על המטרה ששני ניסיונות הצליחו. האדם הראשון פגע בארבעת העיגולים בראש הצלב, ובכך יצר את הריבוע שלו. האדם השני התכוון לפגוע בארבעת העיגולים בזרוע התחתונה, אך היריה השנייה שלו, בצד שמאל, הייתה גבוהה מדי. זה אילץ אותו להשלים את הארבעה שלו בצורה שונה ממה שהוא התכוון. כך ניתן לראות שלמרות שזה לא משנה באיזה עיגול אתה פוגע ביריה הראשונה, היריה השנייה עשויה לחייב אותך לנוהל מוגדר אם אתה רוצה להשיג את הריבוע שלך. כעת, החידה היא לומר בכמה דרכים שונות אפשר ליצור ריבוע על המטרה עם ארבע יריות.
מקורות:נושאים:גאומטריה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
באיור יש לנו מטרה מעט מוזרה שעוצבה על ידי צלף אקסצנטרי. הרעיון שלו היה שכדי לצבור ניקוד, עליך לפגוע בארבעה עיגולים בארבע יריות כך שאותן ארבע יריות ייצרו ריבוע. ניתן לראות מהתוצאות שנרשמו על המטרה ששני ניסיונות הצליחו. האדם הראשון פגע בארבעת העיגולים בראש הצלב, ובכך יצר את הריבוע שלו. האדם השני התכוון לפגוע בארבעת העיגולים בזרוע התחתונה, אך היריה השנייה שלו, בצד שמאל, הייתה גבוהה מדי. זה אילץ אותו להשלים את הארבעה שלו בצורה שונה ממה שהוא התכוון. כך ניתן לראות שלמרות שזה לא משנה באיזה עיגול אתה פוגע ביריה הראשונה, היריה השנייה עשויה לחייב אותך לנוהל מוגדר אם אתה רוצה להשיג את הריבוע שלך. כעת, החידה היא לומר בכמה דרכים שונות אפשר ליצור ריבוע על המטרה עם ארבע יריות.
מקורות:נושאים:גאומטריה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 284