Beno Arbel Olympiad, 2019, 8th grade

• 问题 1

  一行中按升序排列着六个连续的自然数。第一个数的数字之和为 40，且最后一个数的数字之和为 18，这有可能吗？

  主题：

  数论 -> 模算术/余数算术 -> 整除规则 组合数学 -> 案例分析/检查案例 -> 过程/程序

• 问题 2

  找出最小的数 `c`，使得方程 `3x + 4y = c` 恰好有 3 个正整数解。

  主题：

  数论 代数学 -> 方程 -> 丢番图方程
  其他来源：
  • Beno Arbel Olympiad, 2019, 7th grade 问题 5

• 问题 3

  将图中的形状分成7个全等的部分。
  

  主题：

  几何学 组合数学 -> 组合几何学 -> 切割图形/分割问题

• 问题 4

  哪个更大，大多少倍：
  `(1 + 2/3) (2 + 3/4) ... (998 + 999/1000)` 或者 `(3 + 2/1) (4 + 3/2) ... (1000 + 999/998)`

  主题：

  算术 代数学 -> 数列 代数学 -> 代数技巧 -> 裂项求和
  其他来源：
  • Beno Arbel Olympiad, 2019, 7th grade 问题 6

• 问题 5

  在图中绘制了一个梯形，在其每个底边上选择了 5 个点。这些点的一部分通过直线段连接。证明蓝色区域的面积之和等于橙色区域的面积之和。
  

  主题：

  几何学 -> 面积计算 几何学 -> 平面几何学 -> 三角形

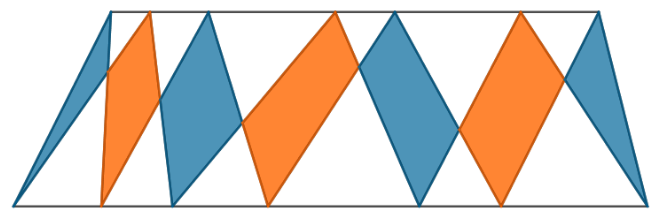
• 问题 6

  桌子上有100个杯子，里面分别装着`101, 102,...,200`颗珠子。两个人玩以下游戏：每人轮流选择一个杯子，并从中取出任意数量的珠子。如果某个玩家行动后，发现有两个杯子里的珠子数量相同，则该玩家输掉。谁有必胜策略：先手还是后手？

  主题：

  组合数学 -> 不变量 组合数学 -> 博弈论
  其他来源：
  • Beno Arbel Olympiad, 2019, 7th grade 问题 8

• 问题 7

  将字母替换为不同的非零数字，使得等式成立。相同的字母代表相同的数字，不同的字母代表不同的数字；גל和גר是由这些数字组成的两位数。
  `ל \/ ג + ל\/ר + ל\/ב + ל\/(רג) + ל\/ (ל ג) = ל`

  主题：

  数论 代数学 -> 方程 算术 -> 分数 谜题和画谜 -> 重构算式/密码算术
  其他来源：
  • Beno Arbel Olympiad, 2019, 9th grade 问题 6

• 问题 8

  给出5枚外观相同的银币和5枚外观相同的金币。在银币中，有四枚真币，它们的重量相同，还有一枚假币，比真银币重一克。在金币中，有四枚真币，它们的重量相同，还有一枚假币，比真金币轻一克。是否可以用天平称三次，找出这两枚假币？

  主题：

  逻辑学 -> 推理/逻辑 算法理论 -> 称重问题 组合数学 -> 案例分析/检查案例 -> 过程/程序