שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 81 - תשעת האסימונים

    יש לי תשעה אסימונים, שעל כל אחד מהם רשומה אחת מתשע הספרות, `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. סידרתי אותם על השולחן בשתי קבוצות, כפי שניתן לראות באיור, כך שייצרו שני תרגילי כפל, וגיליתי ששני התרגילים נתנו את אותה מכפלה. תגלו ש-`158` כפול `23` זה `3,634`, וגם `79` כפול `46` זה `3,634`. עכשיו, החידה שאני מציע היא לסדר מחדש את האסימונים כך שנקבל את המכפלה הגדולה ביותר האפשרית. מה הדרך הטובה ביותר למקם אותם? זכרו ששתי הקבוצות חייבות להכפיל לאותה כמות, וחייבים להיות שלושה אסימונים כפול שניים במקרה אחד, ושניים כפול שני אסימונים במקרה השני, בדיוק כמו עכשיו.

  • שאלה 82 - עשרת המונים

    במקרה זה אנו משתמשים באפס בנוסף ל-`1, 2, 3, 4, 5, 6, 7, 8, 9`. החידה היא, כבמקרה הקודם, לסדר את עשרת המונים כך שמכפלות שני הכפל יהיו זהות, ואפשר שיהיו ספרה אחת או יותר במכפיל, כרצונך. האמור לעיל הוא הישג קל מאוד; אך נדרש גם למצוא את שני הסידורים הנותנים זוגות של המכפלות הגבוהות והנמוכות ביותר האפשריות. כמובן שיש להשתמש בכל מונה, ולא ניתן למקם את הספרה אפס משמאל לשורת ספרות כאשר אין לה השפעה. שברים פשוטים או עשרוניים אינם מותרים.

  • שאלה 83 - כפל ספרותי

    הנה בעיה משעשעת נוספת עם תשע הספרות, כאשר הספרה אפס אינה נכללת. באמצעות כל ספרה פעם אחת בלבד, אנו יכולים ליצור שני תרגילי כפל בעלי מכפלה זהה, וניתן לעשות זאת בדרכים רבות. לדוגמה, 7x658 ו-14x329 מכילים את כל הספרות פעם אחת, והמכפלה בכל מקרה זהה - `4,606`. כעת, ניתן לראות שסכום הספרות במכפלה הוא `16`, שאינו הסכום הגבוה או הנמוך ביותר שניתן להשיג. האם תוכלו למצוא את הפתרון לבעיה שנותן את הסכום הנמוך ביותר האפשרי של ספרות במכפלה המשותפת? וגם את זה שנותן את הסכום הגבוה ביותר האפשרי?

  • שאלה 84 - החידה של פיירו

    פיירו באיור עומד בתנוחה המייצגת את סימן הכפל. הוא מצביע על העובדה המוזרה ש-`15` כפול `93` מניב בדיוק את אותן הספרות (`1,395`), אך מסודרות באופן שונה. החידה היא לקחת ארבע ספרות כלשהן שתרצו (כולן שונות) ולסדר אותן באופן דומה, כך שהמספר שנוצר מצד אחד של פיירו כאשר הוא מוכפל במספר בצד השני יפיק את אותן הספרות. ישנן דרכים מעטות מאוד לעשות זאת, ואני אתן את כל המקרים האפשריים. האם תוכלו למצוא את כולם? מותר לכם לשים שתי ספרות בכל צד של פיירו כמו בדוגמה המוצגת, או למקם ספרה בודדת בצד אחד ושלוש ספרות בצד השני. אם היינו משתמשים רק בשלוש ספרות במקום בארבע, הדרכים האפשריות היחידות הן אלה: `3` כפול `51` שווה ל-`153`, ו-`6` כפול `21` שווה ל-`126`.

  • שאלה 85 - מספרי המוניות

    שוטר לונדוני ראה לילה אחד שתי מוניות נוסעות לכיוונים מנוגדים בנסיבות חשודות. השוטר הזה היה אדם זהיר ופקחי במיוחד, והוא הוציא את פנקס הכיס שלו כדי לרשום את מספרי המוניות, אך גילה שהוא איבד את העיפרון שלו. למרבה המזל, עם זאת, הוא מצא חתיכת גיר קטנה, שבעזרתה סימן את שני המספרים על שער הכניסה למזח סמוך. כשחזר לאותו מקום במשמרת שלו, הוא עמד והסתכל שוב על המספרים, והבחין בתכונה המוזרה הזו, שכל תשע הספרות (ללא אפס) היו בשימוש וששום ספרה לא חזרה על עצמה, אבל אם הוא יכפיל את שני המספרים זה בזה, הם ייצרו שוב את תשע הספרות, כולן פעם אחת, ורק פעם אחת. כאשר אחד הפקידים הגיע למזח בשעות הבוקר המוקדמות, הוא הבחין בסימני הגיר ומחק אותם בזהירות. מכיוון שהשוטר לא הצליח להיזכר בהם, התייעצו עם מתמטיקאים מסוימים לגבי קיומה של שיטה ידועה לגילוי כל זוגות המספרים בעלי התכונה המוזרה שהשוטר הבחין בה; אך הם לא הכירו שיטה כזו. עם זאת, החקירה הייתה מעניינת, והשאלה הבאה מתוך רבות הוצעה: אילו שני מספרים, המכילים יחד את כל תשע הספרות, יניבו, כאשר יוכפלו זה בזה, מספר אחר (הגבוה ביותר האפשרי) המכיל גם הוא את כל תשע הספרות? האפס אינו מותר בשום מקום.

  • שאלה 86 - כפל מוזר

    אם אני מכפיל `51,249,876` ב-`3` (ובכך משתמש בכל תשע הספרות פעם אחת בלבד), אני מקבל `153,749,628` (שגם הוא מכיל את כל תשע הספרות פעם אחת). באופן דומה, אם אני מכפיל `16,583,742` ב-`9` התוצאה היא `149,253,678`, כאשר בכל מקרה כל תשע הספרות נמצאות בשימוש. כעת, קח `6` כמכפיל שלך ונסה לסדר את שמונה הספרות הנותרות כדי להפיק באמצעות כפל מספר המכיל את כל תשע הספרות פעם אחת בלבד. תגלה שזה לא קל בכלל, אבל אפשר לעשות את זה.
    נושאים:
    אריתמטיקה

  • שאלה 87 - חידת תגי המספרים

    במקום בו מועסקים מספר רב של פועלים בבניין, נהוג לספק לכל אדם דיסקית קטנה הנושאת את מספרו. דיסקיות אלו נתלות על לוח על ידי הפועלים כשהם מגיעים, ומשמשות כמעקב אחר דייקנות. פעם שמתי לב שמנהל עבודה הסיר מספר תגים אלה מהלוח שלו והניח אותם על טבעת מפוצלת שנשא בכיסו. זה מיד נתן לי את הרעיון לחידה טובה. למעשה, אני אספר לקוראים שלי שכך בדיוק עולים רעיונות לחידות. אתה לא יכול באמת ליצור רעיון: זה קורה - ואתה צריך להיות בכוננות כדי לתפוס אותו כשזה קורה.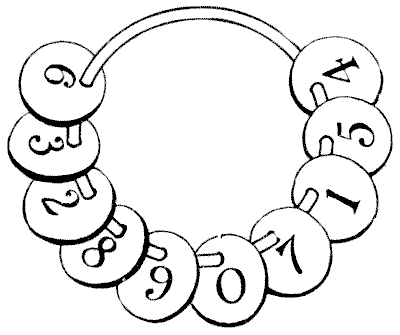 ניתן לראות מהאיור שיש עשרה תגים אלה על טבעת, ממוספרים מ-`1` עד `9` ו-`0`. החידה היא לחלק אותם לשלוש קבוצות מבלי להסיר אף אחד מהם מהטבעת, כך שהקבוצה הראשונה כפול השנייה תיתן את הקבוצה השלישית. לדוגמה, אנו יכולים לחלק אותם לשלוש קבוצות, `2`—`8` `9` `7`—`1` `5` `4` `6` `3`, על ידי הבאת ה-`6` וה-`3` סביב ל-`4`, אבל לצערי שתי הראשונות כשהן מוכפלות יחד לא יוצרות את השלישית. האם אתה יכול להפריד אותם נכון? כמובן שמותר לך שיהיו לך כמה תגים שתרצה בכל קבוצה. החידה דורשת קצת תושייה, אלא אם כן יש לך מזל לפגוע בתשובה במקרה.

  • שאלה 88 - חילוק דיגיטלי

    זוהי חידה טובה נוספת לסדר את תשע הספרות (ללא הספרה אפס) לשתי קבוצות כך שקבוצה אחת, כאשר מחלקים אותה בשנייה, תניב מספר נתון ללא שארית. לדוגמה, `1` `3` `4` `5` `8` חלקי `6` `7` `2` `9` נותן `2`. האם הקורא יכול למצוא סידורים דומים המניבים `3, 4, 5, 6, 7, 8` ו-`9` בהתאמה? כמו כן, האם הוא יכול למצוא את זוגות המספרים הקטנים ביותר האפשריים בכל מקרה? לדוגמה, `1` `4` `6` `5` `8` חלקי `7` `3` `2` `9` נכון באותה מידה עבור `2` כמו הדוגמה האחרת שנתנו, אך המספרים גבוהים יותר.

  • שאלה 89 - חיבור הספרות

    אם ארשום סכום כסף, £`987, 5`s. `4`½d.., ואחבר את הספרות, סכומן הוא `36`. אף ספרה לא נעשה בה שימוש פעם שנייה בסכום או בחיבור. זהו הסכום הגדול ביותר האפשרי בתנאים אלה. כעת מצאו את הסכום הקטן ביותר האפשרי, בלירות, שילינגים, פני ופרטינגים, כאשר כולם מיוצגים. אינכם צריכים להשתמש ביותר מתשע הספרות אם אינכם רוצים, אך אין לחזור על אף ספרה כלל. אסור להשתמש באפס.

  • שאלה 90 - חידת המאה

    האם תוכלו לכתוב `100` בצורה של מספר מעורב, תוך שימוש בכל תשע הספרות פעם אחת בלבד? המתמטיקאי הצרפתי המכובד, אדוארד לוקאס, מצא שבע דרכים שונות לעשות זאת, והביע את ספקותיו לגבי קיומן של דרכים אחרות. למעשה יש בדיוק אחת-עשרה דרכים ולא יותר. הנה אחת מהן, `91 5742/638`. בתשע מהדרכים האחרות יש באופן דומה שתי ספרות בחלק השלם של המספר, אך לביטוי האחד-עשר יש רק ספרה אחת שם. האם הקורא יכול למצוא את הצורה האחרונה הזו?