שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 91 - עוד שברים מעורבים

    כשפרסמתי לראשונה את הפתרון שלי לחידה האחרונה, זה הוביל אותי לנסות לבטא את כל המספרים בזה אחר זה עד `100` על ידי שבר מעורב המכיל את כל תשע הספרות. הנה שנים עשר מספרים שהקורא ינסה את כוחו בהם: `13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94`. השתמשו בכל אחת מתשע הספרות פעם אחת בלבד, בכל מקרה.

  • שאלה 92 - מספרי ריבוע דיגיטליים

    אלה הן תשע הספרות המסודרות כך שהן יוצרות ארבעה מספרי ריבוע: `9, 81, 324, 576`. עכשיו, האם תוכלו לחבר את כולן יחד כדי ליצור מספר ריבוע יחיד - (I) הקטן ביותר האפשרי, ו- (II) הגדול ביותר האפשרי?

  • שאלה 93 - המספר המיסטי אחד עשר

    האם תוכלו למצוא את המספר הגדול ביותר האפשרי המכיל תשע מתוך עשר הספרות (בהתייחסות לאפס כספרה) אשר ניתן לחלק ב-`11` ללא שארית? האם תוכלו למצוא גם את המספר הקטן ביותר האפשרי שנוצר באותו אופן ומתחלק ב-`11`? הנה דוגמה, כאשר הספרה `5` הושמטה: `896743012`. מספר זה מכיל תשע מהספרות ומתחלק ב-`11`, אך הוא אינו המספר הגדול ביותר וגם לא הקטן ביותר שיעבוד.

  • שאלה 94 - המאה הדיגיטלית

    `1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9 = 100`.

    נדרש להציב סימנים אריתמטיים בין תשע הספרות כך שהתוצאה תהיה שווה ל- `100`. כמובן, אסור לשנות את הסדר המספרי הקיים של הספרות. האם תוכלו לתת פתרון נכון המשתמש ב- (`1`) מספר הסימנים המועט ביותר האפשרי, וב- (`2`) מספר המינימלי של קווים או נקודות נפרדים של העט? כלומר, יש צורך להשתמש בכמה שפחות סימנים אפשריים, וסימנים אלה צריכים להיות בצורה הפשוטה ביותר. סימני החיבור והכפל (+ ו- ×) ייחשבו כשני קווים, סימן החיסור (-) כקו אחד, סימן החילוק (÷) כשלושה, וכן הלאה.

  • שאלה 95 - ארבע פעמים שבע

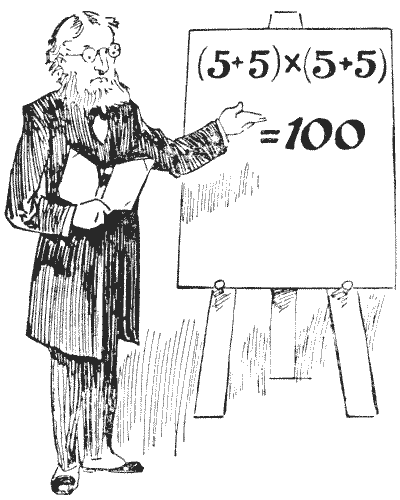    באיור נראה פרופסור ראקבריין מדגים אחד מהתחבולות הקטנות שבהן הוא רגיל לבדר את הכיתה שלו. הוא מאמין שעל ידי הוצאת תלמידיו ממסלולים שחוקים הוא מסוגל יותר להבטיח את תשומת ליבם, ולגרום לשיטות חשיבה מקוריות ומתוחכמות. כפי שנראה, הוא בדיוק הראה כיצד ניתן לכתוב ארבע פעמים `5` עם סימנים אריתמטיים פשוטים כך שיצייגו `100`. כל קורא צעיר יראה במבט חטוף שהדוגמה שלו נכונה לחלוטין. עכשיו, מה שהוא רוצה שתעשו זה: סדרו ארבע פעמים `7` (לא יותר ולא פחות) עם סימנים אריתמטיים כך שהם ייצגו `100`. אם הוא היה אומר שעלינו להשתמש בארבע פעמים `9`, מיד היינו יכולים לכתוב `99 9/9`, אבל ארבע פעמים `7` דורשות קצת יותר תושייה. האם תוכלו לגלות את הטריק הקטן?

  • שאלה 96 - מספרי הקוביות

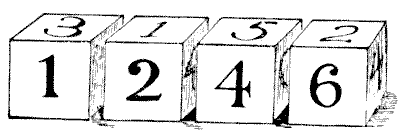
    יש לי סט של ארבע קוביות, שלא מסומנות עם נקודות בצורה רגילה, אלא עם ספרות ערביות, כפי שמוצג באיור. כל קובייה, כמובן, נושאת את המספרים `1` עד `6`. כאשר מצמידים אותן יחד, הן יוצרות מספרים רבים ושונים. כפי שמיוצג, הן מרכיבות את המספר `1246`. עכשיו, אם אני מרכיב את כל המספרים השונים בעלי ארבע ספרות שאפשר ליצור עם הקוביות האלה (אף פעם לא שם את אותה ספרה יותר מפעם אחת באף מספר), לסכום איזה מספר הם יגיעו? מותר לך להפוך את ה-`6` כך שייצג `9`. אני לא מבקש, או מצפה, מהקורא ללכת לכל העבודה של כתיבת הרשימה המלאה של המספרים ואז לחבר אותם. החיים לא ארוכים מספיק בשביל אנרגיה מבוזבזת כזאת. האם אתה יכול להגיע לתשובה בכל דרך אחרת?

  • שאלה 97 - הנקודה על השולחן

    ילד, שחזר לאחרונה מבית הספר, רצה להציג לאביו את פיקחותו. הוא דחף שולחן עגול גדול לפינת החדר, כפי שמוצג באיור, כך שהוא נגע בשני הקירות, ואז הצביע על כתם דיו בקצה השולחן.

     

    "הנה חידה קטנה בשבילך, אבא," אמר הילד. "הנקודה הזו נמצאת בדיוק שמונה אינץ' מקיר אחד ותשעה אינץ' מהקיר השני. האם תוכל לומר לי מה קוטר השולחן מבלי למדוד אותו?"

    הילד נשמע אומר לחבר, "זה ממש ניצח את אבא;" אבל ידוע שהאב העיר למכר בעיר שהוא פתר את העניין בראשו תוך דקה. אני לעתים קרובות תוהה מי דיבר אמת.

  • שאלה 98 - נימוסים אקדמיים

    בבית ספר מעורב מסוים, שבו דגש מיוחד הושם על הקניית נימוסים טובים, היה להם כלל מוזר בהתכנסות בכל בוקר. היו פי שניים בנות מבנים. כל בת קידה לכל בת אחרת, לכל בן ולמורה. כל בן קידה לכל בן אחר, לכל בת ולמורה. בסך הכל נעשו תשע מאות קידות באקדמיה המודל הזו בכל בוקר. עכשיו, האם אתה יכול לומר בדיוק כמה בנים היו בבית הספר?

  • שאלה 99 - שלושים ושלוש הפנינים

    "אדם שאני מכיר," אמר טדי ניקולסון במסיבת משפחה מסוימת, "ברשותו מחרוזת של שלושים ושלוש פנינים. הפנינה האמצעית היא הגדולה והטובה מכולן, והשאר נבחרו וסודרו כך, שמתחילים מקצה אחד, כל פנינה עוקבת שווה £`100` יותר מקודמתה, ישר עד לפנינה הגדולה. מהקצה השני הפנינים עולות בערכן ב-£`150` עד לפנינה הגדולה. כל המחרוזת שווה £`65,000`. מה ערכה של הפנינה הגדולה הזו?"

     

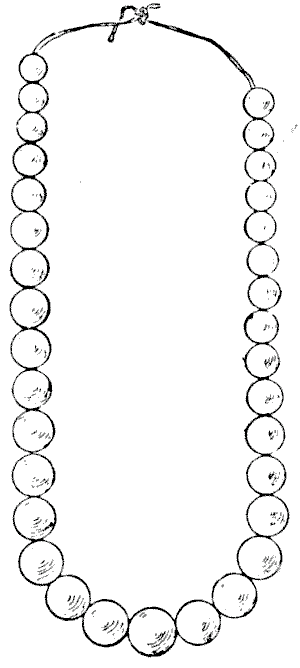
    "פנינים ופריטי לבוש אחרים," אמר הדוד וולטר, כשמחיר הפנינה היקרה התגלה, "מזכירים לי את אדם וחווה. הרשויות, ייתכן שאינכם יודעים, חלוקות לגבי מספר התפוחים שנאכלו על ידי אדם וחווה. יש הסבורים שחווה `8` (אכלה) ואדם `2` (גם), סך הכל `10` בלבד. אבל מתמטיקאים מסוימים חישבו זאת אחרת, וטוענים שחווה `8` ואדם סך הכל `16`. עם זאת, החוקרים האחרונים ביותר חושבים שהמספרים הנ"ל שגויים לחלוטין, כי אם חווה `8` ואדם `82`, הסך הכל חייב להיות `90`."

    "טוב," אמר הארי, "נראה לי שאם היו ענקים בימים ההם, כנראה חווה `81` ואדם `82`, מה שייתן סך של `163`."

    "אני לא מרוצה בכלל," אמרה מוד. "נראה לי שאם חווה `81` ואדם `812`, הם צרכו יחד `893`."

    "אני בטוח שכולכם טועים," התעקש מר וילסון, "כי אני חושב שחווה `814` אדם, ואדם `8124` חווה, אז אנחנו מקבלים סך של `8,938`."

    "אבל, תראו," התפרץ הרברט. "אם חווה `814` אדם ואדם `81242` מחייב את חווה, בטח הסך הכל היה `82,056`!"

    בשלב זה הציע הדוד וולטר שהם יניחו לעניין. הוא הצהיר שזה בבירור מה שמתמטיקאים מכנים בעיה בלתי ניתנת להכרעה.

  • שאלה 100 - החידה של הפועל

    הפרופסור רקבריין, במהלך אחת משיטוטיו, פגש אדם שחופר בור עמוק.

    "בוקר טוב," הוא אמר. "מה העומק של הבור הזה?"

    "נחש," השיב הפועל. "הגובה שלי הוא בדיוק חמש רגל ועשרה אינץ'."

    "כמה עמוק יותר אתה הולך לחפור?" שאל הפרופסור.

    "אני הולך פי שניים יותר עמוק," הייתה התשובה, "ואז הראש שלי יהיה פי שניים רחוק יותר מתחת לאדמה ממה שהוא נמצא עכשיו מעל האדמה."

    עכשיו רקבריין שואל אם תוכלו לומר מה יהיה העומק של הבור הזה כשהוא יסתיים.