שעשועונים במתמטיקה, הנרי ארנסט דודני
-
שאלה 71 - סר אדווין דה טיודור
באיור יש לנו סקיצה של סר אדווין דה טיודור היוצא להציל את אהובתו, איזבלה היפה, אשר הוחזקה בשבי על ידי ברון מרושע שכן. סר אדווין חישב שאם ירכב חמישה עשר מייל לשעה, הוא יגיע לטירה שעה מוקדם מדי, ואילו אם ירכב עשרה מייל לשעה, הוא יגיע לשם שעה אחת מאוחר מדי. כעת, היה זה בעל חשיבות עליונה שהוא יגיע בדיוק בזמן שנקבע, כדי שההצלה שתכנן תצליח, ושעת הפגישה הייתה חמש אחר הצהריים, כאשר הגבירה השבויה תשתה את תה אחר הצהריים שלה. החידה היא לגלות בדיוק כמה רחוק סר אדווין דה טיודור היה צריך לרכב.
-
שאלה 72 - שאלת מטוס הים
תושבי סלוקומב-און-סי התרגשו מאוד מביקורו של איש מעופף מסוים. כל העיר יצאה לראות את טיסתו של מטוס הים המופלא, וכמובן, דובסון ומשפחתו היו שם. מאסטר טומי היה במיטבו, והודיע לאביו שאנגלים הם טייסים טובים יותר מסקוטים ואירים כי הם לא כל כך כבדים. "איך אתה מגיע לזה?" שאל מר דובסון. "ובכן, אתה רואה", ענה טומי, "זה נכון שבאירלנד יש אנשי קורק ובסקוטלנד אנשי אייר, וזה אפילו יותר טוב, אבל באנגליה יש אנשים 'קלים' יותר (lightermen, משחק מילים)." למרבה הצער היה צריך להסביר זאת לגברת דובסון, וזה קצת הוריד מהעניין. טיסת מטוס הים הייתה מסלוקומב לפודלוויל, עיירת נופש שכנה - במרחק של חמישה מיילים. אבל הייתה רוח חזקה, שעזרה לטייס כל כך שהוא עשה את המסע החוצה בזמן קצר של עשר דקות, אם כי לקח לו שעה לחזור לנקודת ההתחלה בסלוקומב, כשהרוח מנוגדת לו לחלוטין. עכשיו, כמה זמן היו לוקחות לו עשרת המיילים האלה אם היה שקט מוחלט? כמובן, מנוע מטוס הים פעל באופן אחיד לאורך כל הדרך. -
שאלה 73 - רכיבה על חמור
במהלך ביקור בחוף הים, טומי ואוונג'לין התעקשו לערוך מרוץ חמורים לאורך מסלול של מייל אחד על החול. מר דובסון וכמה מחבריו שפגש על החוף שימשו כשופטים, אך מכיוון שהחמורים היו מכרים מוכרים וסירבו להיפרד לאורך כל הדרך, תיקו היה בלתי נמנע. עם זאת, השופטים, שהוצבו בנקודות שונות במסלול, שסומן ברבעי מיילים, רשמו את התוצאות הבאות: – שלושת הרבעים הראשונים רצו בשש ושלושת רבעי דקות, חצי המייל הראשון לקח את אותו הזמן כמו החצי השני, והרבע השלישי רץ בדיוק באותו הזמן כמו הרבע האחרון. מתוצאות אלו, מר דובסון שעשע את עצמו בגילוי בדיוק כמה זמן לקח לשני החמורים האלה לרוץ את כל המייל. האם תוכל לתת את התשובה? -
שאלה 74 - סל תפוחי האדמה
לאיש היה סל ובו חמישים תפוחי אדמה. הוא הציע לבנו, כמעט שעשוע, שהוא יניח את תפוחי האדמה הללו על הקרקע בקו ישר. המרחק בין תפוח האדמה הראשון לשני יהיה יארד אחד, בין השני לשלישי שלושה יארדים, בין השלישי לרביעי חמישה יארדים, בין הרביעי לחמישי שבעה יארדים, וכן הלאה - עלייה של שני יארדים עבור כל תפוח אדמה עוקב שיונח. לאחר מכן הילד ירים אותם ויכניס אותם לסל אחד בכל פעם, כאשר הסל ממוקם ליד תפוח האדמה הראשון. כמה רחוק יצטרך הילד לנסוע כדי להשלים את המשימה של איסוף כולם? לא נתייחס למסע הכרוך בהנחת תפוחי האדמה, כך שהוא מתחיל מהסל כשהם כולם פרוסים. -
שאלה 75 - תעריף הנסיעה של הנוסע
מבט ראשון לא היה מעלה על הדעת שיש מקום למחלוקת בשאלה הכלולה בתקרית הקטנה הבאה, אך לשני האנשים המעורבים לקח זמן מה להגיע להסכמה. מר סמית'רס שכר מכונית כדי לקחת אותו מאדלפורד לקלינקרביל וחזרה תמורת £`3`. בבייקנהם, בדיוק באמצע הדרך, הוא אסף מכר, מר טומפקינס, והסכים לקחת אותו לקלינקרביל ולהחזיר אותו לבייקנהם בנסיעה חזרה. כמה הוא היה צריך לגבות מהנוסע? זאת השאלה. מה היה תעריף סביר עבור מר טומפקינס?
נושאים:אלגברה -> בעיות מילוליות -
שאלה 76 - חבית הבירה
אדם קנה כמות מוזרה של יין בחביות וחבית אחת המכילה בירה. אלה מוצגים באיור, המסומנים במספר הגלונים שכל חבית הכילה. הוא מכר כמות מהיין לאדם אחד וכמות כפולה לאחר, אך שמר את הבירה לעצמו. החידה היא לציין איזו חבית מכילה בירה. האם אתה יכול לומר איזו מהן זו? כמובן, האיש מכר את החביות בדיוק כפי שקנה אותן, מבלי לתפעל בשום צורה את התכולה.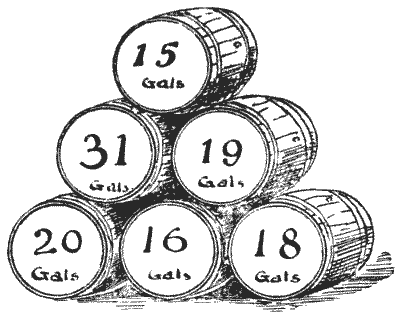
נושאים:אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 אלגברה -> בעיות מילוליות לוגיקה -> הגיון -
שאלה 77 - ספרות וריבועים
ניתן לראות בתרשים שסידרנו את תשע הספרות בריבוע כך שהמספר בשורה השנייה גדול פי שניים מהמספר בשורה הראשונה, והמספר בשורה התחתונה גדול פי שלושה מהמספר בשורה העליונה. ישנן שלוש דרכים נוספות לסדר את הספרות כך שיתקבל אותו פתרון. האם תוכלו למצוא אותן?
נושאים:אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה קומבינטוריקה -> בדיקת מקרים -> תהליכים -
שאלה 78 - ספרות זוגיות ואי-זוגיות
הספרות האי-זוגיות, `1, 3, 5, 7`, ו-`9`, מסתכמות ל-`25`, בעוד שהספרות הזוגיות, `2, 4, 6`, ו-`8`, מסתכמות רק ל-`20`. סדרו את הספרות האלה כך שהספרות האי-זוגיות והזוגיות יסתכמו באופן שווה. שברים מורכבים, שברים לא אמיתיים ושברים עשרוניים מחזוריים אינם מותרים. -
שאלה 79 - חידת הלוקרים
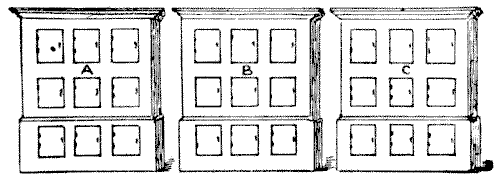
לאיש היו במשרדו שלושה ארונות, שבכל אחד מהם תשעה לוקרים, כפי שמוצג בדיאגרמה. הוא הורה לפקיד שלו להציב ספרה שונה על כל לוקר בארון A, ולעשות את אותו הדבר בארון B ובארון C. מכיוון שמותר לנו כאן לקרוא לאפס ספרה, ולא נאסר עליו להשתמש באפס כמספר, ברור שהייתה לו האפשרות להשמיט כל אחת מעשר הספרות מכל ארון.
כעת, המעסיק לא אמר שהלוקרים ימוספרו בסדר מספרי כלשהו, והוא הופתע לגלות, לאחר שהעבודה הסתיימה, שהספרות כנראה עורבבו באופן אקראי. כשקרא לפקיד שלו להסבר, הנער האקסצנטרי הצהיר שהעלתה בדעתו המחשבה לסדר את הספרות כך שבכל מקרה הן יצרו תרגיל חיבור פשוט, כאשר שתי השורות העליונות של הספרות יוצרות את הסכום בשורה התחתונה. אבל הנקודה המפתיעה ביותר הייתה זו: שהוא סידר אותן כך שהחיבור ב-A נתן את הסכום הקטן ביותר האפשרי, שהחיבור ב-C נתן את הסכום הגדול ביותר האפשרי, וכי כל תשע הספרות בסך הכל בשלושת הסכומים היו שונות. החידה היא להראות כיצד ניתן לעשות זאת. אין לאפשר עשרונים והאפס אינו יכול להופיע במקום המאות.
-
שאלה 80 - שלוש הקבוצות
בכתב העת "Nouvelles Annales de Mathématiques" הופיעה החידה הבאה כשינוי לאחת מ"חידות קנטרברי" שלי. סדר את תשע הספרות בשלוש קבוצות של שתיים, שלוש וארבע ספרות, כך ששני המספרים הראשונים כאשר מכפילים אותם זה בזה יוצרים את השלישי. לדוגמה, `12` × `483` = `5,796`. אני מציע כעת לכלול גם את המקרים שבהם יש ספרה אחת, ארבע וארבע ספרות, כגון `4` × `1,738` = `6,952`. האם תוכל למצוא את כל הפתרונות האפשריים בשני המקרים?