תורת המספרים, חלוקה

חילוק היא אחת מארבע פעולות החשבון הבסיסיות, המייצגת חלוקת כמות לחלקים שווים או מציאת מספר הפעמים שמספר אחד מוכל באחר. שאלות כוללות ביצוע חילוק, הבנת מושגים כמו מחולק, מחלק, מנה ושארית, ופתרון בעיות מילוליות קשורות.

• הספרות שהתחפשו

  בתרגיל החילוק שלפניכם, (כמעט) כל הספרות התחפשו!

  מהו המספר המחולק?

  \(\begin{align*} &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }**\text{ }8**\\ &\overline{* * * * * * *\text{ } *}| * *\text{ } *\\ &\underline{\text{ }\text{ }* *\text{ } *}\\ &\text{ }\text{ }\text{ }\text{ }\text{ }* * * *\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\underline{\text{ }\text{ }* *\text{ } *}\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }* * * *\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\underline{* * *\text{ } *}\\ \end{align*}\)

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה חידות ורבוסים -> שחזרו את התרגיל
  מקורות:
  • תחרות החידמטיקה השבועית של בר אילן, 2024 שאלה 8

• שאלה

  על הלוח כתובים כל המספרים מ-1 עד `10^9` (כולל `10^9`). המספרים שמתחלקים ב-3 כתובים באדום, ושאר המספרים בכחול. סכום של כל המספרים האדומים שווה ל- `X`, וסכום של כל המספרים הכחולים שווה ל- `Y`. איזה מספר גדול יותר, `2X` או `Y`, ובכמה?

  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 לוגיקה -> הגיון אלגברה -> סדרות אלגברה -> אי שוויונים -> ממוצעים תורת המספרים -> חלוקה
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 2

• הבקר של ג'אדקינס

  היירם ב. ג'אדקינס, סוחר בקר מטקסס, היו לו חמש עדרי חיות, שהורכבו משוורים, חזירים וכבשים, עם אותו מספר חיות בכל עדר. בוקר אחד הוא מכר את כל מה שהיה לו לשמונה סוחרים. כל סוחר קנה את אותו מספר חיות, שילם שבעה עשר דולר עבור כל שור, ארבעה דולר עבור כל חזיר ושני דולר עבור כל כבש; והיירם קיבל בסך הכל שלוש מאות ואחד דולר. מהו המספר הגדול ביותר של חיות שיכל להיות לו? וכמה יהיו מכל סוג?
  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה אלגברה -> בעיות מילוליות תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 35

• שק האגוזים

  לשלושה בנים ניתנה שקית אגוזים כמתנת חג המולד, והוסכם שהם יחולקו ביחס לגילם, שביחד הסתכם ל-`17 1/2` שנים. עכשיו השק הכיל `770` אגוזים, וכאשר הרברט לקח ארבעה, רוברט לקח שלושה, וכאשר הרברט לקח שישה, כריסטופר לקח שבעה. החידה היא לגלות כמה אגוזים היו לכל אחד, ומה היו הגילאים של הבנים.

  נושאים:

  אלגברה -> בעיות מילוליות אריתמטיקה -> שברים אלגברה -> אי שוויונים -> ממוצעים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 50

• תעלומת רציף ופשו

  הייתה מהומה גדולה ברחוב תמזה התחתון בבוקר ה-`12` בינואר `1887`. כאשר חברי הצוות המוקדמים הגיעו לרציף ופשו, הם גילו שהכספת נפרצה, סכום כסף ניכר נלקח והמשרדים היו במצב של אי סדר גדול. השומר הלילי לא היה בשום מקום, אבל אף אחד שהכיר אותו לרגע לא חשד בו שהוא אשם בשוד. באמונה זו אושרה דעתם של הבעלים כאשר, מאוחר יותר באותו יום, הם קיבלו הודעה שגופתו של המסכן נמצאה על ידי משטרת הנהר. סימני אלימות מסוימים הצביעו על העובדה שהוא הותקף באכזריות והושלך לנהר. שעון שנמצא בכיסו נעצר, כפי שקורה תמיד בנסיבות כאלה, וזה היה רמז רב ערך לשעת הפשע. אבל קצין טיפש מאוד (ואנחנו תמיד מוצאים אינדיבידואלים טיפשים אחד או שניים בגופים האינטליגנטיים ביותר של אנשים) למעשה שעשע את עצמו על ידי סיבוב המחוגים שוב ושוב, מנסה להפעיל את השעון שוב. לאחר שננזף בחריפות על שיקול הדעת החמור הזה, הוא נשאל אם הוא זוכר את השעה שהוצגה על ידי השעון כשנמצא. הוא השיב שהוא לא זוכר, אבל הוא נזכר שמחוג השעות ומחוג הדקות היו בדיוק ביחד, אחד מעל השני, ומחוג השניות בדיוק עבר את השנייה הארבעים ותשע. יותר מזה הוא לא זכר.

  מה הייתה השעה המדויקת שבה נעצר השעון של השומר? מניחים כמובן שהשעון היה מדויק.

  נושאים:

  לוגיקה -> הגיון אריתמטיקה -> שברים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 60

• עשרת המונים

  במקרה זה אנו משתמשים באפס בנוסף ל-`1, 2, 3, 4, 5, 6, 7, 8, 9`. החידה היא, כבמקרה הקודם, לסדר את עשרת המונים כך שמכפלות שני הכפל יהיו זהות, ואפשר שיהיו ספרה אחת או יותר במכפיל, כרצונך. האמור לעיל הוא הישג קל מאוד; אך נדרש גם למצוא את שני הסידורים הנותנים זוגות של המכפלות הגבוהות והנמוכות ביותר האפשריות. כמובן שיש להשתמש בכל מונה, ולא ניתן למקם את הספרה אפס משמאל לשורת ספרות כאשר אין לה השפעה. שברים פשוטים או עשרוניים אינם מותרים.
  נושאים:

  אריתמטיקה קומבינטוריקה -> בדיקת מקרים -> תהליכים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 82

• חילוק דיגיטלי

  זוהי חידה טובה נוספת לסדר את תשע הספרות (ללא הספרה אפס) לשתי קבוצות כך שקבוצה אחת, כאשר מחלקים אותה בשנייה, תניב מספר נתון ללא שארית. לדוגמה, `1` `3` `4` `5` `8` חלקי `6` `7` `2` `9` נותן `2`. האם הקורא יכול למצוא סידורים דומים המניבים `3, 4, 5, 6, 7, 8` ו-`9` בהתאמה? כמו כן, האם הוא יכול למצוא את זוגות המספרים הקטנים ביותר האפשריים בכל מקרה? לדוגמה, `1` `4` `6` `5` `8` חלקי `7` `3` `2` `9` נכון באותה מידה עבור `2` כמו הדוגמה האחרת שנתנו, אך המספרים גבוהים יותר.
  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 88

• ארבע פעמים שבע

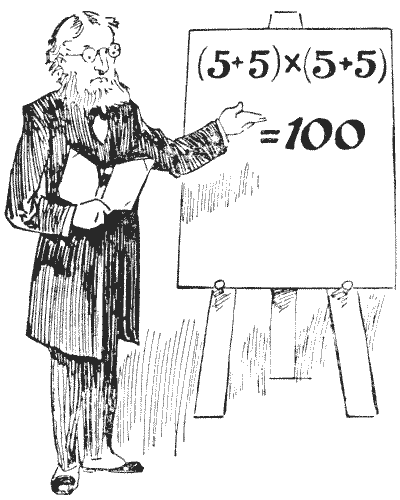  באיור נראה פרופסור ראקבריין מדגים אחד מהתחבולות הקטנות שבהן הוא רגיל לבדר את הכיתה שלו. הוא מאמין שעל ידי הוצאת תלמידיו ממסלולים שחוקים הוא מסוגל יותר להבטיח את תשומת ליבם, ולגרום לשיטות חשיבה מקוריות ומתוחכמות. כפי שנראה, הוא בדיוק הראה כיצד ניתן לכתוב ארבע פעמים `5` עם סימנים אריתמטיים פשוטים כך שיצייגו `100`. כל קורא צעיר יראה במבט חטוף שהדוגמה שלו נכונה לחלוטין. עכשיו, מה שהוא רוצה שתעשו זה: סדרו ארבע פעמים `7` (לא יותר ולא פחות) עם סימנים אריתמטיים כך שהם ייצגו `100`. אם הוא היה אומר שעלינו להשתמש בארבע פעמים `9`, מיד היינו יכולים לכתוב `99 9/9`, אבל ארבע פעמים `7` דורשות קצת יותר תושייה. האם תוכלו לגלות את הטריק הקטן?

  נושאים:

  אלגברה -> משוואות אריתמטיקה -> שברים תורת המספרים -> חלוקה חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 95

• מורשת מבלבלת

  אדם הוריש מאה דונם אדמה לחלוקה בין שלושת בניו - אלפרד, בנימין וצ'ארלס - ביחס של שליש, רבע וחמישית בהתאמה. אבל צ'ארלס נפטר. איך יש לחלק את האדמה בצורה הוגנת בין אלפרד ובנימין?
  נושאים:

  אלגברה -> בעיות מילוליות אריתמטיקה -> שברים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 112

• כפל פשוט

  אם נמספר שישה כרטיסים `1, 2, 4, 5, 7`, ו-`8`, ונניח אותם על השולחן בסדר הזה:—

  `1\ \ \ 4\ \ \ 2\ \ \ 8\ \ \ 5\ \ \ 7`

  אנו יכולים להדגים שכדי להכפיל ב-`3` כל מה שצריך זה להעביר את ה-`1` לקצה השני של השורה, וזהו. התשובה היא `428571`. האם תוכלו למצוא מספר שכאשר מכפילים אותו ב-`3` ומחלקים ב-`2`, התשובה תהיה זהה כאילו הסרנו את הכרטיס הראשון (שבמקרה הזה צריך להיות `3`) מתחילת השורה לסופה?

  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 126