קומבינטוריקה

קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.

עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות

  • המונים הצבעוניים

    הדיאגרמה מייצגת עשרים וחמישה מונים צבעוניים: אדום, כחול, צהוב, כתום וירוק (המצוינים על ידי האותיות הראשונות שלהם), וישנם חמישה מכל צבע, ממוספרים `1, 2, 3, 4` ו-`5`. הבעיה היא לסדר אותם בריבוע כך שאף צבע או מספר לא יחזרו על עצמם באף אחת מחמש השורות, חמש העמודות ושני האלכסונים. האם תוכלו לסדר אותם מחדש? מקורות:

  • אומנות ליקוק הבולים העדינה

    חוק הביטוח הוא מקור פורה ביותר לפאזלים משעשעים, במיוחד משעשעים אם אתה במקרה נמנה עם הפטורים. ההקדמה של אדם לאומנות ליקוק הבולים העדינה מעלה את החידה הקטנה הבאה: אם יש לך כרטיס המחולק לשישה עשר מקומות (`4` × `4`), ומסופקים לך שפע של בולים בערכים של `1`d., `2`d., `3`d., `4`d., ו-`5`d., מהו הערך הגדול ביותר שתוכל להדביק על הכרטיס אם שר האוצר אוסר עליך להניח בול בקו ישר (כלומר, אופקית, אנכית או אלכסונית) עם בול אחר בעל ערך דומה? כמובן, ניתן להדביק רק בול אחד במקום אחד. הקורא כנראה יגלה, כשהוא יראה את הפתרון, שבדומה לבולים עצמם, הוא הוכה. סביר להניח שיחסרו לו שני פני מהמקסימום. חבר שאל את הדואר כיצד ניתן לעשות זאת; אך הם שלחו אותו לפקיד המכס והבלו, ששלח אותו לנציבי הביטוח, ששלחו אותו לאגודה מאושרת, אשר שלחה אותו בחילול קודש - אך לא משנה. מקורות:

  • ארבעים ותשעה האסימונים

    האם תוכלו לסדר מחדש את ארבעים ותשעה האסימונים שלמעלה בריבוע כך שאף אות, וגם אף מספר, לא יהיו באותו קו עם אחד דומה, אנכית, אופקית או אלכסונית? כאן אני, כמובן, מתכוון לקווים המקבילים לאלכסונים, במובן של לוח השחמט. מקורות:

  • שלוש הכבשים

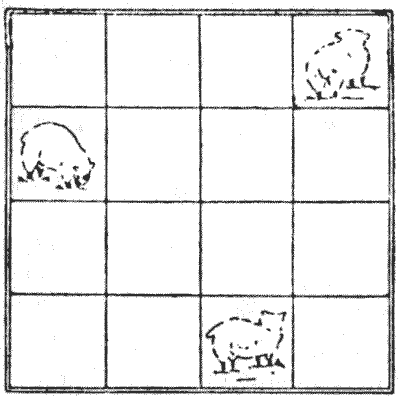    לחקלאי היו שלוש כבשים וסידור של שש עשרה מכלאות, המחולקות על ידי גדרות באופן המצוין באיור. בכמה דרכים שונות הוא יכול למקם את הכבשים האלה, כל אחת במכלאה נפרדת, כך שכל מכלאה תהיה מאוכלסת או בשורה (אופקית, אנכית או אלכסונית) עם כבשה אחת לפחות? נתתי סידור אחד שמקיים את התנאים. כמה אחרים אתה יכול למצוא? אין לספור היפוכים ושיקופים כדברים שונים. הקורא רשאי להתייחס לכבשים כמלכות. הבעיה היא אז למקם את שלוש המלכות כך שכל משבצת תהיה מאוכלסת או מותקפת על ידי מלכה אחת לפחות - במספר המרבי של דרכים שונות. מקורות:

  • חידת חמשת הכלבים

    בשנת `1863`, סי. אף. דה יאניש דן לראשונה ב"חידת חמש המלכות" - להציב חמש מלכות על לוח השחמט כך שכל משבצת תותקף או תאוכלס - אשר הוצעה על ידי חברו, "מר דה ר.". יאניש הראה שאם אף מלכה לא יכולה לתקוף מלכה אחרת, ישנן תשעים ואחת דרכים שונות להציב את חמש המלכות, כאשר היפוכים ושיקופים אינם נחשבים כשונים. אם המלכות יכולות לתקוף זו את זו, תיעדתי מאות דרכים, אך לא ניתן למנות אותן במדויק.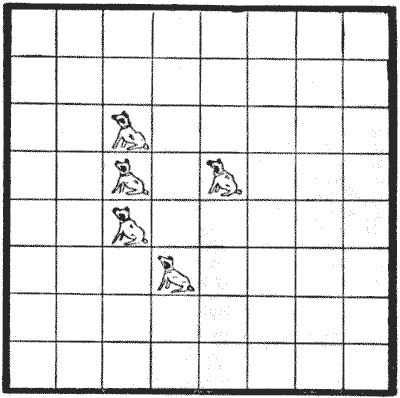 האיור אמור לייצג סידור של שישים וארבעה מְלוּנוֹת. ניתן לראות שחמש מְלוּנוֹת מכילות כל אחת כלב, ובבדיקה נוספת ניתן לראות שכל אחת משישים וארבע המְלוּנוֹת נמצאת בקו ישר עם לפחות כלב אחד - או אופקית, אנכית או באלכסון. קח כל מְלוּנָה שתרצה, ותגלה שתוכל למתוח קו ישר לכלב באחת משלוש הדרכים שהוזכרו. החידה היא להחליף את חמשת הכלבים ולגלות בכמה דרכים שונות ניתן להציב אותם בחמש מְלוּנוֹת בשורה ישרה, כך שכל מְלוּנָה תמיד תהיה בקו אחד עם לפחות כלב אחד. היפוכים ושיקופים נחשבים כאן כשונים. מקורות:

  • סהרוני הירח של ביזנטיון

    כאשר פיליפוס ממקדוניה, אביו של אלכסנדר הגדול, מצא עצמו ניצב בפני קשיים גדולים במצור על ביזנטיון, הוא הורה לאנשיו לחתור תחת החומות. אולם, משאלותיו סוכלו, שכן לא חלף זמן רב לאחר תחילת הפעולות, עד שסהר ירח הופיע לפתע בשמים וחשף את תוכניותיו בפני יריביו. הביזנטים שמחו מטבע הדברים, וכדי להביע את הכרת התודה שלהם הקימו פסל לדיאנה, והסהר הפך מאז לסמל המדינה. במקדש שהכיל את הפסל הייתה רצפה מרובעת שהורכבה משישים וארבעה אריחים גדולים ויקרים. כולם היו פשוטים, למעט חמישה, שנשאו את סמל הסהר. חמשת אלה הוצבו מסיבות נסתרות כך שכל אריח יהיה תחת השגחה (כלומר, בקו ישר, אנכית, אופקית או אלכסונית) של לפחות אחד מהסהרונים. הסידור שאומץ על ידי האדריכל הביזנטי היה כדלקמן:—

     

    כעת, כיסוי אחד מחמשת הסהרונים הללו היה עבירה חמורה, שהעונש עליה היה מוות מכאיב וממושך מאוד. אבל לרגל חגיגה מסוימת היה צורך להניח על המרצפת הזו שטיח מרובע בגודל המרבי האפשרי, והראיתי באיור על ידי הצללה כהה את הממדים הגדולים ביותר שיהיו זמינים.

    החידה היא להראות כיצד האדריכל, אילו חזה את שאלת השטיח הזו, יכול היה לסדר את חמשת אריחי הסהר שלו בהתאם לתנאים הנדרשים, ובכל זאת לאפשר הנחת שטיח מרובע גדול ככל האפשר מבלי שאף אחד מחמשת אריחי הסהר יכוסה, או כל חלק מהם.

    מקורות:

  • חידת מלכות ורץ

    יובחן שכל משבצת בלוח היא תפוסה או מותקפת. החידה היא להחליף רץ בצריח באותה המשבצת, ואז להניח את ארבע המלכות על משבצות אחרות כך שכל משבצת שוב תהיה תפוסה או מותקפת.

    מקורות:

  • הצלב הדרומי

     

    באיור לעיל יש לנו חמישה כוכבי לכת ושמונים ואחד כוכבים קבועים, כאשר חמישה מהאחרונים מוסתרים על ידי כוכבי הלכת. ניתן לראות שכל כוכב, למעט עשרת הכוכבים שיש להם נקודה שחורה במרכזם, נמצא בקו ישר, אנכית, אופקית או באלכסון, עם לפחות אחד מכוכבי הלכת. החידה היא לסדר מחדש את כוכבי הלכת כך שכל הכוכבים יהיו בקו אחד עם אחד או יותר מהם.

    בסידור מחדש של כוכבי הלכת, כל אחד מחמשתם עשוי לנוע פעם אחת בקו ישר, בכל אחד משלושת הכיוונים שהוזכרו. הם, כמובן, יסתירו חמישה כוכבים אחרים במקום אלה המכוסים כעת.

    מקורות:

  • חידת יתדות הכובעים

    הנה חידה בת חמש מלכות שהצגתי בצורה דמיונית בשנת `1897`. מכיוון שהמלכות יוצגו שם ככובעים על שישים וארבעה יתדות, אדבוק בכותרת, "חידת יתדות הכובעים". ניתן לראות שכל משבצת מאוכלסת או מותקפת. החידה היא להעביר מלכה אחת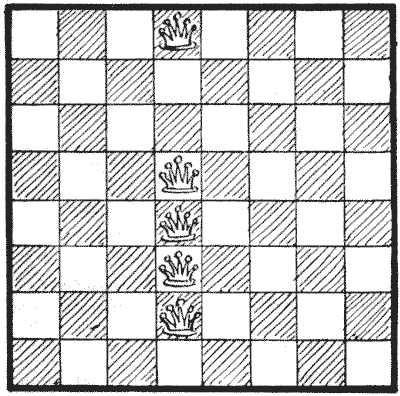 למשבצת אחרת כך שעדיין כל משבצת תהיה מאוכלסת או מותקפת, לאחר מכן להעביר מלכה שנייה בתנאים דומים, לאחר מכן מלכה שלישית, ולבסוף מלכה רביעית. לאחר המסע הרביעי כל משבצת חייבת להיות מותקפת או מאוכלסת, אך אף מלכה לא תתקוף מלכה אחרת. כמובן, שהמסעים לא חייבים להיות "מסעי מלכה"; ניתן להעביר מלכה לכל חלק בלוח. מקורות:

  • חידה עם חיילים

    הנח שני חיילים באמצע לוח השחמט, אחד ב-Q `4` והשני ב-K `5`. כעת, הנח את ארבעה-עשר החיילים הנותרים (שישה-עשר בסך הכל) כך שאף שלושה לא יהיו בקו ישר בכל כיוון אפשרי.

    שים לב שאני בכוונה לא אומר מלכות, מכיוון שעל ידי המילים "בכל כיוון אפשרי" אני חורג מעבר להתקפות על אלכסונים. יש להתייחס לחיילים כנקודות בלבד במרחב - במרכזי הריבועים. ראה קווים מנוקדים במקרה של מס' `300`, "שמונה מלכות."

    מקורות: