קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
ציד אריות
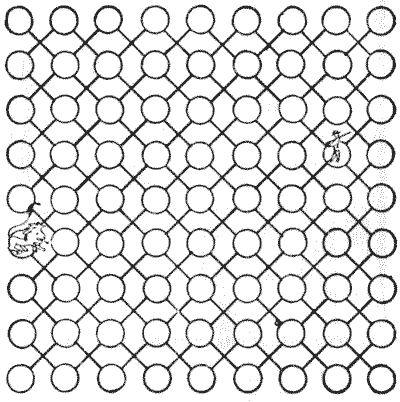
חברי, קפטן פות'ם הול, צייד חיות גדולות ידוע, אומר שאין דבר מלהיב יותר ממפגש עם עדר—להקה—צוות—מִשְׁפָּחָה—נחיל (לקח לי רבע שעה שלמה להיזכר במילה הנכונה, אבל סוף סוף מצאתי אותה)—גאווה של אריות. מדוע מספר אריות נקרא "גאווה," מספר לווייתנים נקרא "בית ספר," ומספר שועלים נקרא "רמייה" הן תעלומות של פילולוגיה שאליהן לא אכנס.
ובכן, הקפטן אומר שאם אריה נמרץ חוצה את דרכך במדבר, זה נהיה תוסס, כי האריה בדרך כלל חיפש את האדם בדיוק כמו שהאדם חיפש את מלך היער. ובכל זאת כשהם נפגשים הם תמיד רבים ונלחמים. קצת התבוננות בסכסוך המצער והמתמשך הזה בין שתי משפחות מכובדות הובילה אותי להבין כמה חישובים לגבי הסבירות שהאדם והאריה יחצו זה את דרכו של זה בג'ונגל. בכל המקרים הללו צריך להתחיל בהנחות מסוימות פחות או יותר שרירותיות. לכן באיור לעיל חשבתי לנכון לייצג את השבילים במדבר בסדר מופתי כזה. למרות שהקפטן מבטיח לי שעקבות האריות בדרך כלל רצים בדרך הזו, יש לי ספקות.
החידה היא פשוט לגלות בכמה דרכים שונות ניתן להציב את האדם והאריה בשני מקומות שונים שאינם על אותו נתיב. על ידי "נתיבים" יש להבין שאני מתייחס רק לקווים המצוירים. לפיכך, למעט ארבע הנקודות הפינתיות, כל לוחם נמצא תמיד בשני נתיבים ולא יותר. ניתן לראות שיש הרבה מקום להתחמק זה מזה במדבר, וזה בדיוק מה שתמיד הבינו.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 318
-
שומרי האבירים
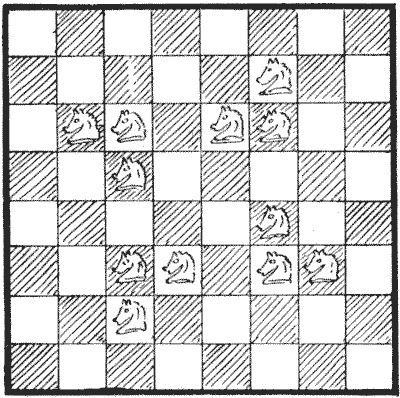
האביר הוא הקומיקאי הנמוך חסר האחריות של לוח השחמט. "הוא נוכל מאוד לא בטוח, מתגנב ומדכא," אומר סופר אמריקאי. "הוא יכול לזוז רק שני ריבועים, אך מפצה על כמות התנועה שלו באיכותה, שכן הוא יכול לקפוץ ריבוע אחד הצידה ואחד קדימה בו זמנית, כמו חתול; יכול לעמוד על רגל אחת באמצע הלוח ולקפוץ לכל אחד משמונת הריבועים שהוא בוחר; יכול לעלות על צד אחד של גדר ולהשמיץ שלושה או ארבעה אנשים בצד השני; יש לו דרך מעוררת התנגדות להכניס את עצמו למקומות בטוחים שבהם הוא יכול להפחיד את המלך ולאלץ אותו לזוז, ואז לטרוף מלכה. לרוע טהור אין לאביר שווה, וכאשר אתה רודף אחריו מחור אחד הוא קופץ לאחר." נעשו ניסיונות שוב ושוב להשיג הגדרה קצרה, פשוטה ומדויקת של תנועת האביר—ללא הצלחה. זה באמת מורכב מלהזיז ריבוע אחד כמו צריח, ואז ריבוע אחר כמו רץ—שני הפעולות נעשות בקפיצה אחת, כך שלא משנה אם הריבוע הראשון שעוברים עליו תפוס על ידי כלי אחר או לא. זו, למעשה, התנועה הקופצת היחידה בשחמט. אבל קשה ככל שיהיה להגדיר, ילד יכול ללמוד את זה על ידי הסתכלות תוך מספר דקות.
הראיתי בתרשים כיצד ניתן להציב שנים עשר אבירים (המספר הקטן ביותר האפשרי שיבצע את המשימה) על לוח השחמט כך שכל ריבוע יהיה או תפוס או מותקף על ידי אביר. בחן כל ריבוע בתורו, ותגלו שזה כך. כעת, החידה במקרה זה היא לגלות מהו המספר הקטן ביותר האפשרי של אבירים הנדרש כדי שכל ריבוע יהיה או תפוס או מותקף, וכל אביר מוגן על ידי אביר אחר. ואיך הייתם מסדרים אותם? יתברר שמתוך שנים עשר המוצגים בתרשים רק ארבעה מוגנים כך על ידי היותם במרחק מהלך של אביר מאביר אחר.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 319
-
מסע הצריח
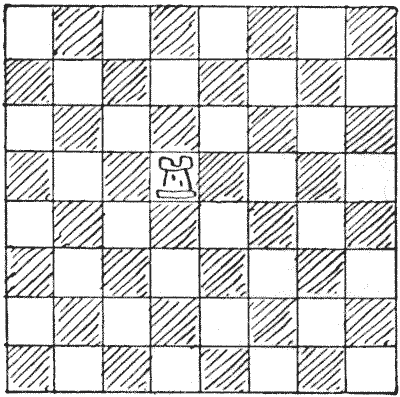 החידה היא להזיז את הצריח הבודד על פני כל הלוח, כך שהוא יבקר בכל משבצת בלוח פעם אחת בלבד, ויסיים את מסעו במשבצת ממנה הוא התחיל. עליכם לעשות זאת במספר המהלכים המינימלי האפשרי, ואם לא תהיו זהירים מאוד, תבצעו מהלך אחד יותר מדי. כמובן, משבצת נחשבת כ"מבוקרת" בין אם רק עוברים מעליה או הופכים אותה לתחנת עצירה, ולא נתווכח על הנקודה האם המשבצת המקורית מבוקרת פעמיים בפועל. נניח שהיא לא.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
החידה היא להזיז את הצריח הבודד על פני כל הלוח, כך שהוא יבקר בכל משבצת בלוח פעם אחת בלבד, ויסיים את מסעו במשבצת ממנה הוא התחיל. עליכם לעשות זאת במספר המהלכים המינימלי האפשרי, ואם לא תהיו זהירים מאוד, תבצעו מהלך אחד יותר מדי. כמובן, משבצת נחשבת כ"מבוקרת" בין אם רק עוברים מעליה או הופכים אותה לתחנת עצירה, ולא נתווכח על הנקודה האם המשבצת המקורית מבוקרת פעמיים בפועל. נניח שהיא לא.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 320
-
מסע הצריח
אני קורא לחידה הזו "מסע הצריח", מכיוון שהמילה "tour" (הנגזרת מגלגל של חרט) מרמזת שאנו חוזרים לנקודה ממנה יצאנו, ואנו לא עושים זאת במקרה הזה. לא נהיה מרוצים מסיור חג מודרך אישית שהסתיים בכך שהשאיר אותנו, למשל, באמצע הסהרה. הצריח כאן עושה עשרים ואחד מהלכים, שבמהלכם הוא מבקר בכל משבצת בלוח פעם אחת בלבד, ועוצר במשבצת המסומנת `10` בסוף המהלך העשירי שלו, ומסתיים במשבצת המסומנת `21`. שני מהלכים רצופים אינם יכולים להתבצע באותו כיוון - כלומר, עליך לבצע פנייה לאחר כל מהלך.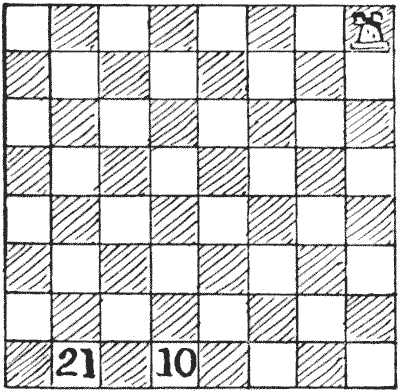 מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 321
-
העלמה הדועכת
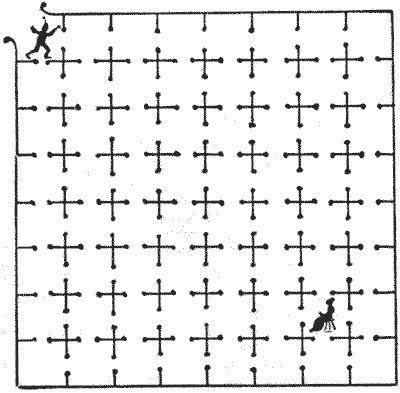 ברון מרושע בימים הטובים של פעם כלא עלמה חפה מפשע באחד הצינוקים העמוקים ביותר מתחת לחפיר הטירה. ניתן לראות מהאיור שלנו שהיו שישים ושלושה תאים בצינוק, כולם מחוברים בדלתות פתוחות, והעלמה הייתה כבולה בתא שבו היא מוצגת. כעת, אביר אמיץ, שאהב את העלמה, הצליח להציל אותה מהאויב. לאחר שהשיג כניסה לצינוק בנקודה שבה הוא נראה, הוא הצליח להגיע לעלמה לאחר שנכנס לכל תא פעם אחת בלבד. קחו את העיפרון שלכם ונסו להתחקות אחר מסלול כזה. לאחר שהצלחתם, נסו לגלות מסלול בעשרים ושניים נתיבים ישרים דרך התאים. ניתן לעשות זאת במספר הזה מבלי להיכנס לאף תא פעם שנייה.
מקורות:
ברון מרושע בימים הטובים של פעם כלא עלמה חפה מפשע באחד הצינוקים העמוקים ביותר מתחת לחפיר הטירה. ניתן לראות מהאיור שלנו שהיו שישים ושלושה תאים בצינוק, כולם מחוברים בדלתות פתוחות, והעלמה הייתה כבולה בתא שבו היא מוצגת. כעת, אביר אמיץ, שאהב את העלמה, הצליח להציל אותה מהאויב. לאחר שהשיג כניסה לצינוק בנקודה שבה הוא נראה, הוא הצליח להגיע לעלמה לאחר שנכנס לכל תא פעם אחת בלבד. קחו את העיפרון שלכם ונסו להתחקות אחר מסלול כזה. לאחר שהצלחתם, נסו לגלות מסלול בעשרים ושניים נתיבים ישרים דרך התאים. ניתן לעשות זאת במספר הזה מבלי להיכנס לאף תא פעם שנייה.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 322
-
חידת מבוך
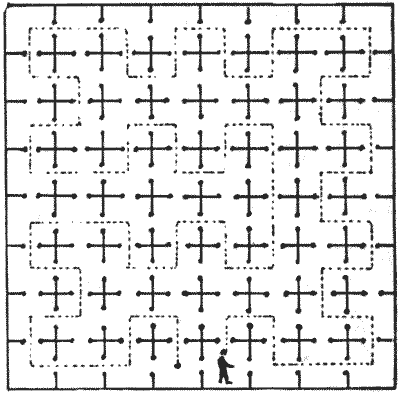 אסיר צרפתי, בשל חטאיו (או חטאיהם של אחרים), נכלא במבוך תת-קרקעי המכיל שישים וארבעה תאים, שכולם מתקשרים עם פתחי דלתות פתוחים, כפי שמוצג באיור שלנו. כדי להפחית את השעמום של חייו המוגבלים, הוא הציב לעצמו חידות שונות, וזו אחת מהן. החל מהתא שבו הוא מוצג, כיצד הוא יכול לבקר בכל תא פעם אחת, ורק פעם אחת, ולבצע כמה שיותר פניות? הניסיון הראשון שלו מוצג על ידי המסלול המקווקו. יתברר שיש לא פחות מחמישים וחמישה קווים ישרים בנתיב שלו, אבל אחרי ניסיונות רבים הוא השתפר בכך. האם אתה יכול להשיג יותר מחמישים וחמישה? אתה רשאי לסיים את הנתיב שלך בכל תא שתרצה. נסה את החידה עם עיפרון על דיאגרמות של לוח שחמט, או שאתה יכול להתייחס אליהם כאל מסעי צריחים על לוח.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
אסיר צרפתי, בשל חטאיו (או חטאיהם של אחרים), נכלא במבוך תת-קרקעי המכיל שישים וארבעה תאים, שכולם מתקשרים עם פתחי דלתות פתוחים, כפי שמוצג באיור שלנו. כדי להפחית את השעמום של חייו המוגבלים, הוא הציב לעצמו חידות שונות, וזו אחת מהן. החל מהתא שבו הוא מוצג, כיצד הוא יכול לבקר בכל תא פעם אחת, ורק פעם אחת, ולבצע כמה שיותר פניות? הניסיון הראשון שלו מוצג על ידי המסלול המקווקו. יתברר שיש לא פחות מחמישים וחמישה קווים ישרים בנתיב שלו, אבל אחרי ניסיונות רבים הוא השתפר בכך. האם אתה יכול להשיג יותר מחמישים וחמישה? אתה רשאי לסיים את הנתיב שלך בכל תא שתרצה. נסה את החידה עם עיפרון על דיאגרמות של לוח שחמט, או שאתה יכול להתייחס אליהם כאל מסעי צריחים על לוח.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 323
-
האריה והאיש
במקום ציבורי ברומא עמד פעם בית כלא המחולק לשישים וארבעה תאים, כולם פתוחים לשמים וכולם מתקשרים זה עם זה, כפי שמוצג באיור. הספורט שהתקיים כאן נצפה ממגדל גבוה. המשחק האהוב היה להציב נוצרי בתא פינתי אחד ואריה בתא הפינתי הנגדי באלכסון, ואז להשאיר אותם עם כל הדלתות הפנימיות פתוחות. התוצאה הנובעת מכך הייתה לעיתים קרובות מצחיקה ביותר. באחד המקרים קיבל האיש חרב. הוא לא היה פחדן, והיה להוט למצוא את האריה בדיוק כפי שהאריה ללא ספק היה להוט למצוא אותו.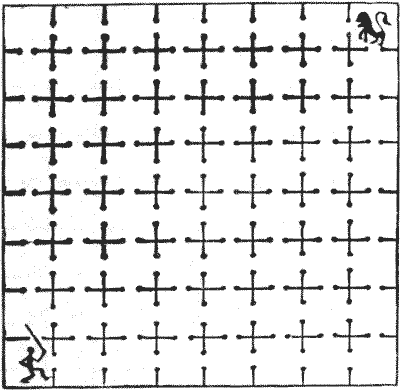 האיש ביקר בכל תא פעם אחת בלבד במספר הקטן ביותר האפשרי של קווים ישרים עד שהגיע לתא של האריה. האריה, באופן מוזר, גם הוא ביקר בכל תא פעם אחת בלבד במספר הקטן ביותר האפשרי של קווים ישרים עד שהגיע לבסוף לתא של האיש. הם התחילו יחד והלכו באותה מהירות; עם זאת, למרות שהם מדי פעם ראו זה את זה, הם מעולם לא נפגשו. החידה היא להראות את המסלול שכל אחד מהם עשה.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
האיש ביקר בכל תא פעם אחת בלבד במספר הקטן ביותר האפשרי של קווים ישרים עד שהגיע לתא של האריה. האריה, באופן מוזר, גם הוא ביקר בכל תא פעם אחת בלבד במספר הקטן ביותר האפשרי של קווים ישרים עד שהגיע לבסוף לתא של האיש. הם התחילו יחד והלכו באותה מהירות; עם זאת, למרות שהם מדי פעם ראו זה את זה, הם מעולם לא נפגשו. החידה היא להראות את המסלול שכל אחד מהם עשה.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 324
-
ביקור אפיסקופלי
המשבצות הלבנות על לוח השחמט מייצגות את הקהילות של דיוקסיה. הניחו את הרץ על כל משבצת שתרצו, ותכננו כך ש (תוך שימוש בתנועת הרץ הרגילה בשחמט) הוא יבקר בכל אחת מהקהילות שלו במספר המהלכים המועט ביותר האפשרי. כמובן, כל הקהילות שעוברים דרכן בכל מהלך נחשבות כ"ביקורות". אתם יכולים לבקר בכל משבצת יותר מפעם אחת, אך אסור לכם לנוע פעמיים בין אותן שתי משבצות סמוכות. מהו מספר המהלכים המועט ביותר האפשרי? הרץ לא צריך לסיים את ביקורו בקהילה ממנה יצא לדרך לראשונה.מקורות:נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> תורת המשחקים קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 325
-
חידת מונה חדשה
הנה חידה חדשה עם הזזת מונים, או מטבעות, שמבט ראשון נראית כאילו היא פשוטה באופן אבסורדי. אבל יתברר שהיא מעט מבלבלת. אני מציג אותה כאן מסיבה שאסביר כשאגיע לחידה הבאה. העתק את הדיאגרמה הפשוטה, מוגדלת, על דף נייר; ואז הנח שני מונים לבנים על הנקודות `1` ו-`2`, ושני מונים אדומים על `9` ו-`10`. החידה היא לגרום לאדומים ולבנים להחליף מקומות. אתה רשאי להזיז את המונים אחד בכל פעם בכל סדר שתרצה, לאורך הקווים מנקודה לנקודה, עם ההגבלה היחידה שמונה אדום ולבן לעולם לא יעמדו בבת אחת על אותו קו ישר. לכן המהלך הראשון יכול להיות רק מ-`1` או `2` ל-`3`, או מ-`9` או `10` ל-`7`.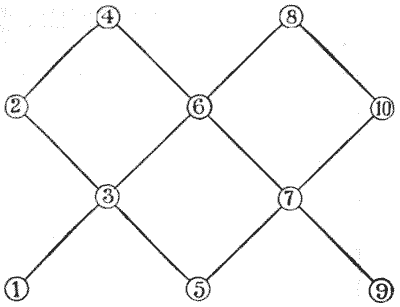 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 326
-
החידה החדשה של הרץ

זוהי חידה קטנה ומסקרנת למדי. הניחו שמונה רצים (ארבעה שחורים וארבעה לבנים) על לוח השחמט המצומצם, כפי שמוצג באיור. הבעיה היא לגרום לרצים השחורים להחליף מקומות עם הלבנים, כך שאף רץ לא יתקוף רץ אחר מצבע מנוגד. הם חייבים לנוע לחלופין—תחילה רץ לבן, אחר כך רץ שחור, אחר כך רץ לבן, וכן הלאה. כאשר תצליחו לעשות זאת בכלל, נסו למצוא את מספר המהלכים המינימלי האפשרי.
אם תוציאו את הרצים שעומדים על משבצות שחורות, ותשחקו רק על המשבצות הלבנות, תגלו שהחידה האחרונה שלי הסתובבה על צידה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 327