קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
סיור המלכה
החידה של ביצוע סיור שלם בלוח השחמט עם המלכה במספר המהלכים המועט ביותר האפשרי (שבו ניתן לבקר בריבועים יותר מפעם אחת) ניתנה לראשונה על ידי סם לויד המנוח ב-אסטרטגיית שחמט שלו. אבל הפתרון המוצג להלן הוא זה שהוא נתן ב-אגוזי שחמט אמריקאים ב-`1868`. תיעדתי לפחות שישה פתרונות שונים במספר המינימלי של מהלכים - ארבעה עשר - אבל זה הטוב מכולם, מסיבות שאסביר.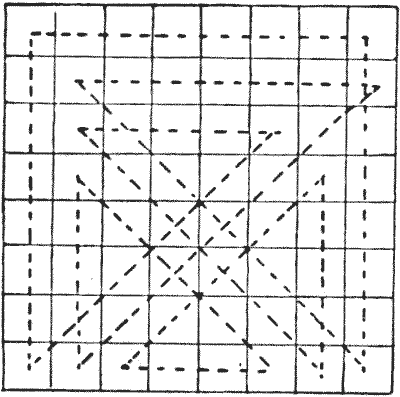 אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: -
אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: - 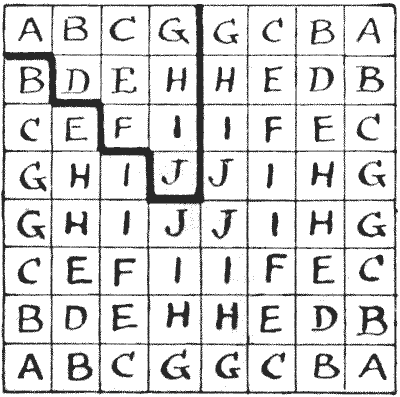 התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת המשחקים קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים
התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת המשחקים קומבינטוריקה -> צביעות -> צביעת שחמט חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 328
-
פאזל הכוכבים

הניחו את חוד העיפרון שלכם על אחד הכוכבים הלבנים ו(מבלי להרים את העיפרון מהדף) מחקו את כל הכוכבים בארבעה עשר קווים ישרים רציפים, כשאתם מסיימים בכוכב הלבן השני. הקווים הישרים שלכם יכולים להיות בכל כיוון שתרצו, רק כל פנייה חייבת להתבצע על כוכב. אין התנגדות למחוק כוכב כלשהו יותר מפעם אחת.
במקרה הזה, כאשר ריבועי ההתחלה והסיום שלכם מקובעים בצורה לא נוחה, אינכם יכולים להשיג פתרון על ידי שבירת מסע מלכה, או בכל דרך אחרת באמצעות מסעי מלכה בלבד. אבל מותר לכם להשתמש בקווים ישרים אלכסוניים —כגון מהכוכב הלבן העליון ישירות לכוכב פינתי.
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 329
-
מרוץ היאכטות
ובכן, יא יבשושים, הניפו את המפרשים הקדמיים הקטנים שלכם, שלפו את הספינקרים, שחררו את יריעות הבלון והכינו את מפרשי הראש שלכם!
המרוץ שלנו מורכב מלהתחיל מהנקודה שבה היאכטה נמצאת באיור ולגעת בכל אחד משישים וארבעת המצופים בארבעה-עשר מסלולים ישרים, ולחזור בזיגזג הסופי למצוף ממנו התחלנו. המסלול השביעי חייב להסתיים במצוף שעליו מתנוסס דגל.
חידה זו תדרוש מיומנות ימית רבה בשל הזוויות החדות שבהן יהיה צורך לעיתים לעשות זיגזג. חוד של עיפרון ועין ימית טובה הם כל הציוד שאנו זקוקים לו.
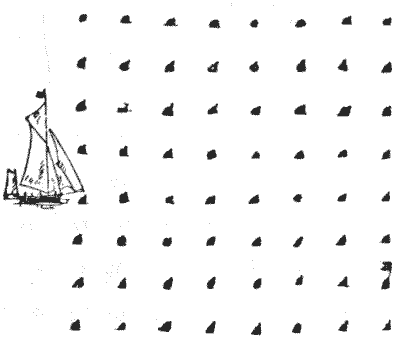
זה קשה, בגלל התנאי לגבי מצוף הדגל, ובגלל שזהו מסלול חוזר. אבל שוב מותרים לנו הקווים האלכסוניים האלה.
מקורות:נושאים:גאומטריה -> גאומטריה במישור -> חשבון זוויות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 330
-
המחליקן המדעי

ניתן לראות שהמחליקן סימן על הקרח שישים וארבע נקודות או כוכבים, והוא מציע להתחיל מהמיקום הנוכחי שלו ליד הפינה ולהיכנס לכל אחת מהנקודות בארבעה עשר קווים ישרים. איך הוא יעשה זאת? כמובן שאין התנגדות לכך שהוא יעבור על פני כל נקודה יותר מפעם אחת, אבל המהלך הישר האחרון שלו חייב להחזיר אותו למיקום שממנו הוא התחיל.
זה רק עניין של לקחת את העיפרון ולהתחיל מהמקום שבו רגלו של המחליקן נחה כרגע, ולמחוק את כל הכוכבים בארבעה עשר קווים ישרים רצופים, ולחזור לנקודה ממנה יצאתם.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 331
-
ארבעים ותשעה הכוכבים
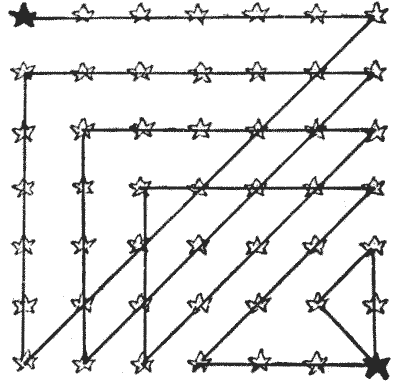 החידה במקרה זה היא פשוט לקחת את העיפרון שלך, ולהתחיל מכוכב שחור אחד, למחוק את כל הכוכבים בשנים עשר קווים ישרים, ולסיים בכוכב השחור השני. ניתן לראות שהניסיון המוצג באיור דורש חמישה עשר קווים. האם אתה יכול לעשות זאת בשנים עשר? כל פנייה חייבת להתבצע על כוכב, והקווים חייבים להיות מקבילים לצדדים ולאלכסונים של הריבוע, כפי שמוצג. במקרה זה אנו עוסקים בלוח שחמט בעל ממדים מופחתים, אך נדרשים רק מהלכי מלכה (מבלי לצאת מגבולות הלוח, כפי שהיה במקרה האחרון).
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים
החידה במקרה זה היא פשוט לקחת את העיפרון שלך, ולהתחיל מכוכב שחור אחד, למחוק את כל הכוכבים בשנים עשר קווים ישרים, ולסיים בכוכב השחור השני. ניתן לראות שהניסיון המוצג באיור דורש חמישה עשר קווים. האם אתה יכול לעשות זאת בשנים עשר? כל פנייה חייבת להתבצע על כוכב, והקווים חייבים להיות מקבילים לצדדים ולאלכסונים של הריבוע, כפי שמוצג. במקרה זה אנו עוסקים בלוח שחמט בעל ממדים מופחתים, אך נדרשים רק מהלכי מלכה (מבלי לצאת מגבולות הלוח, כפי שהיה במקרה האחרון).
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 332
-
מסעה של המלכה
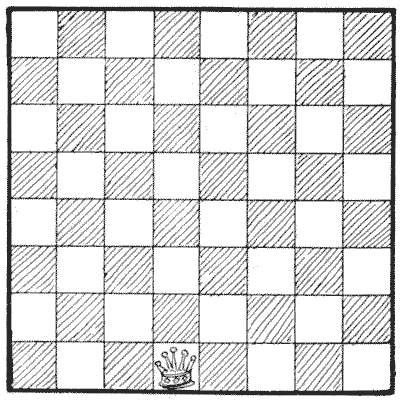 הניחו את המלכה על המשבצת שלה, כפי שמוצג באיור, ואז נסו לגלות את המרחק הגדול ביותר שהיא יכולה לעבור על הלוח בחמישה מהלכי מלכה מבלי לעבור על אף משבצת בפעם השנייה. סמנו את נתיב המלכה על הלוח, ושימו לב היטב גם לכך שאסור לה לחצות את המסלול שלה. זה נראה פשוט מספיק, אבל הקורא עשוי לגלות שהוא נכשל.
מקורות:
הניחו את המלכה על המשבצת שלה, כפי שמוצג באיור, ואז נסו לגלות את המרחק הגדול ביותר שהיא יכולה לעבור על הלוח בחמישה מהלכי מלכה מבלי לעבור על אף משבצת בפעם השנייה. סמנו את נתיב המלכה על הלוח, ושימו לב היטב גם לכך שאסור לה לחצות את המסלול שלה. זה נראה פשוט מספיק, אבל הקורא עשוי לגלות שהוא נכשל.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 333
-
סנט ג'ורג' והדרקון
 הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת.
מקורות:
הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 334
-
שדות התירס של החוואי לורנס
אחד האזורים היפים ביותר בקרבת לונדון לטיול קיץ הוא אותו חלק של בקינגהאמשייר המכונה עמק הצ'ס—לפחות, כך היה לפני כמה שנים, לפני שנתגלה על ידי הקבלן הספקולטיבי. בתחילת המאה הנוכחית חי, לא רחוק מלטיימרס, חקלאי מכובד אך תמהוני בשם לורנס. אחד הרעיונות המוזרים שלו היה שכל אדם שגר ליד גדות נהר הצ'ס צריך להיות בדרך כלשהי בקיא במשחק האצילי באותו שם, וכדי להטביע עובדה זו על אנשיו ושכניו הוא אימץ לעתים טרמינולוגיה מוזרה. לדוגמה, כאשר אחת הכבשות שלו הציגה לו טלה, הוא היה אומר שהיא "הכתירה רגלי"; כאשר הוא הקים אסם חדש מול הכביש המהיר, הוא כינה זאת "הצרחה בצד המלך"; וכאשר הוא שלח אדם עם אקדח כדי להרחיק את הציפורים של שכנו משדותיו, הוא דיבר על זה כ"תקיפת הצריחים של יריבו". כולם בשכונה נהגו להתבדר מהבדיחות הקטנות של החוואי לורנס, ונער אחד (הליצן של הכפר) שספג משיכות אוזניים מהג'נטלמן הזקן על שגנב את ה"ערמונים" שלו הרחיק לכת עד כדי כך שכינה אותו "מגן שחמט זקן ומטופש!"
באחת השנים היה לו שדה מרובע גדול המחולק לארבעים ותשעה מגרשים מרובעים, כפי שמוצג באיור. הריבועים הלבנים נזרעו בחיטה והריבועים השחורים בשעורה. כשמגיע זמן הקציר הוא נתן הוראה שאנשיו יחתכו תחילה את התירס בחלקה המסומנת `1`, וכי כל חיתוך עוקב יהיה בדיוק מהלך פרש מהאחרון, החיתוך השלושה עשר יהיה בחלקה המסומנת `13`, העשרים וחמישי בחלקה המסומנת `25`, השלושים ושבעה בזו המסומנת `37`, והאחרון, או ארבעים ותשעה, בחלקה המסומנת `49`. זה היה יותר מדי עבור הודג' המסכן, ובכל יום החוואי לורנס היה צריך לרדת לשדה ולהראות על איזה חלק צריך להפעיל. אבל הבעיה אולי לא תציג קושי לקוראים שלי.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 335
-
חידת הגרייהאונד
בחידה זו, עשרים המכלאות אינן מתקשרות זו עם זו באמצעות דלתות, אלא מחולקות על ידי קיר נמוך. הדייר הבודד הוא הגרייהאונד שגר במכלאה בפינה השמאלית העליונה. כאשר ניתנת לו החופש, עליו להשיג אותו על ידי ביקור בכל מכלאה פעם אחת בלבד בסדרת מהלכי פרש, תוך סיום בפינה הימנית התחתונה, הפתוחה לעולם. הקווים בדיאגרמה לעיל מראים פתרון אחד. החידה היא לגלות בכמה דרכים שונות יכול הגרייהאונד לצאת כך ממכלאת הפינה שלו.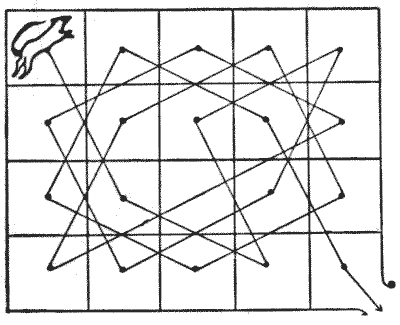 מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים
מקורות:נושאים:קומבינטוריקה -> בדיקת מקרים -> תהליכים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 336
-
ארבעת הקנגורו
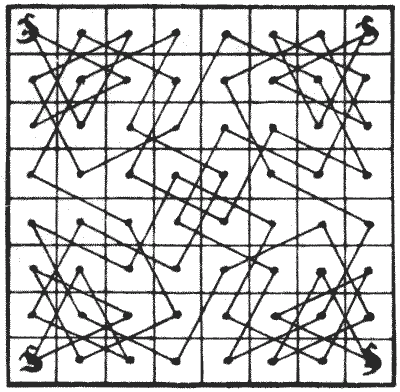 בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.
בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.החידה היא פשוטה. בוקר אחד כל קנגורו יצא לקפיצת הבוקר שלו, ובשש עשרה קפיצות פרש רצופות ביקר בחמישה עשר שדות שונים וחזר לפינה שלו. אף שדה לא ביקר על ידי יותר מאחד הקנגורו. הדיאגרמה מראה כיצד הם הסדירו את העניינים. מה שמבקשים מכם לעשות הוא להראות כיצד הם יכלו לבצע את המעשה מבלי שאף קנגורו יחצה את הקו האופקי באמצע הריבוע שמחלק את הלוח לשני חלקים שווים.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 337