גאומטריה, גאומטריה במרחב

גאומטריה במרחב, או גאומטריה תלת-ממדית, מתמקדת בצורות תלת-ממדיות כגון קוביות, כדורים, גלילים, חרוטים ופאונים. שאלות כוללות בדרך כלל חישוב שטחי פנים ונפחים שלהם, הבנת תכונותיהם והדמיית יחסים ביניהם במרחב תלת-ממדי.

פאונים

  • הבעיה של הפסל

    פסל קדום הוזמן לספק שני פסלים, כל אחד על גבי כן מעוקב. אנו עוסקים בכנים אלה. הם היו בגדלים שונים, כפי שניתן לראות באיור, וכאשר הגיע הזמן לתשלום התגלעה מחלוקת בשאלה האם ההסכם התבסס על מדידה קווית או מעוקבת. אך ברגע שהם באו למדוד את שני הכנים, העניין הוסדר מיד, מכיוון שמספר הרגליים הקווי היה זהה בדיוק למספר הרגליים המעוקב. החידה היא למצוא את המידות לשני כנים בעלי תכונה זו, במספרים הקטנים ביותר האפשריים. אתם מבינים, אם שני הכנים, למשל, מודדים `3` רגל ו-`1` רגל בכל צד, אז המדידה הקווית תהיה `4` רגל והתכולה המעוקבת `28` רגל, שאינם זהים, כך שהמידות האלה לא יתאימו. מקורות:

  • קופסת הקרטון

    חידה זו אינה קשה, אך יהיה משעשע לגלות את הכלל הפשוט לפתרונה. יש לי קופסת קרטון מלבנית. לשטח החלק העליון `120` אינץ' רבוע, לשטח הצד `96` אינץ' רבוע, ולשטח הקצה `80` אינץ' רבוע. מהם הממדים המדויקים של הקופסה? מקורות:

  • בעיית הכדור

     

    יום אחד, סתת היה עסוק בחיתוך כדור עגול לצורך קישוט ארכיטקטוני, כשנער חכם הגיע למקום.

    "תראה," אמר הסתת, "נראה שאתה בחור פיקח, תוכל להגיד לי את זה? אם אניח את הכדור הזה על הקרקע הישרה, כמה כדורים אחרים באותו גודל אוכל להניח סביבו (גם על הקרקע) כך שכל כדור ייגע בכדור הזה?"

    הילד מיד נתן את התשובה הנכונה, ואז הפנה לסתת את השאלה הקטנה הזו:—

    "אם שטח הפנים של הכדור הזה הכיל בדיוק אותו מספר של רגל רבוע כמו שנפחו הכיל רגל מעוקב, מה יהיה אורך הקוטר שלו?"

    הסתת לא הצליח לתת תשובה. האם הייתם יכולים לענות נכון לשאלות של הסתת והילד?

    מקורות:

  • חידה על עפיפון

    בעודי מלווה את ידידי, פרופסור הייפלייט, בתחרות הטסת עפיפונים מדעית בגבעות הדרומיות של סאסקס, נקלעתי לחישוב קטן שאמור לעניין את קוראיי. הפרופסור פרש את החוט שאליו היה מחובר העפיפון שלו מכננת שעליה הוא גולגל בצורה כדורית לחלוטין. כדור חוט זה היה בדיוק שני רגל בקוטר, ולחוט היה קוטר של מאיות אינץ'. מה היה אורך החוט?

    עכשיו, שאלה קטנה ופשוטה כזו שכולם יכולים להבין לחלוטין תגרום לרבים להתקשות לענות בכל דרך שהיא. בואו נראה אם, מבלי להיכנס לחישובים מתמטיים מעמיקים כלשהם, נוכל לקבל את התשובה בערך - נניח, בטווח של מייל אחד ממה שנכון! נניח שכאשר החוט מגולגל כולו הכדור מוצק לחלוטין לכל אורכו, ואין צורך להתחשב בציר שעובר דרכו. עם הפשטה זו, אני תוהה כמה קוראים יכולים לציין אפילו בטווח של מייל אחד מהתשובה הנכונה את אורך החוט הזה.

    מקורות:

  • חידת החרוט

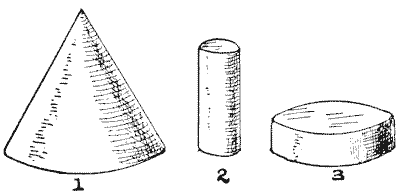    יש לי חרוט עץ, כפי שמוצג באיור `1`. איך עליי לחתוך ממנו את הגליל הגדול ביותר האפשרי? ניתן לראות שאני יכול לחתוך אחד שהוא ארוך ודק, כמו באיור `2`, או קצר ועבה, כמו באיור `3`. אבל אף אחד מהם אינו הגדול ביותר האפשרי. ילד יכול לומר לכם היכן לחתוך, אם הוא היה מכיר את הכלל. האם תוכלו למצוא את הכלל הפשוט הזה? מקורות:

  • חידת החבית

    האנשים באיור מתווכחים על תכולת הנוזל בחבית. אי אפשר לדעת מהו הנוזל הספציפי, מכיוון שאיננו יכולים להסתכל לתוך החבית; לכן נקרא לו מים. איש אחד אומר שהחבית מלאה ביותר מחציה, ואילו השני מתעקש שהיא לא מלאה בחציה. מהי הדרך הקלה ביותר שלהם ליישב את המחלוקת? אין צורך להשתמש במקל, חוט או כלי מדידה מכל סוג שהוא. אני נותן זאת רק כאחת הדוגמאות הפשוטות ביותר לערך של תושייה רגילה בפתרון חידות. בעיות שנראות קשות מאוד ניתנות לעתים קרובות לפתרון בצורה קלה דומה אם רק נשתמש קצת בהיגיון ישר. מקורות:

  • פאזל אריזה

    כפי שכולנו יודעים מניסיון, לעתים קרובות נדרשת תושייה רבה באריזת חפצים לקופסה, אם לא רוצים לבזבז מקום שלא לצורך. אדם סיפר לי פעם שהיו לו מספר רב של כדורי ברזל, שקוטרם בדיוק שני אינץ' כל אחד, והוא רצה לארוז כמה שיותר מהם לתוך קופסה מלבנית באורך `24` `9/10` אינץ', ברוחב `22` `4/5` אינץ' ובעומק `14` אינץ'. מהו המספר הגדול ביותר של כדורים שהוא יכול לארוז בקופסה הזו? מקורות:

  • חמש פרוטות

    הנה חידה קשה במיוחד, ולמרות זאת התנאים שלה פשוטים באופן מגוחך. כל קורא יודע איך להניח ארבע פרוטות כך שהן יהיו במרחק שווה זו מזו. כל שעליכם לעשות הוא לסדר שלוש מהן שטוחות על השולחן כך שהן יגעו זו בזו בצורת משולש, ולהניח את הפרוטה הרביעית מעל במרכז. אז, מכיוון שכל פרוטה נוגעת בכל פרוטה אחרת, כולן נמצאות במרחקים שווים זו מזו. עכשיו נסו לעשות את אותו הדבר עם חמש פרוטות - הניחו אותן כך שכל פרוטה תיגע בכל פרוטה אחרת - ותגלו שזה עניין שונה לחלוטין. מקורות:

  • הבלוק המשולב

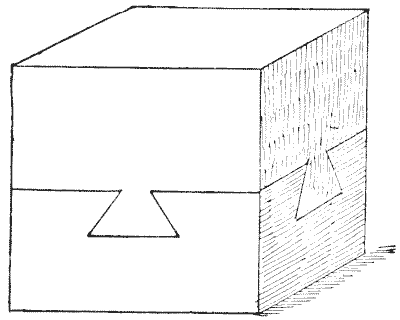    הנה חידה מכנית מוזרה שקיבלתי לפני כמה שנים, אבל אני לא יכול לומר מי המציא אותה לראשונה. היא מורכבת משני גושי עץ מלאים המשולבים זה בזה היטב. בשני הצדדים האנכיים האחרים שאינם נראים, המראה זהה בדיוק לאלה המוצגים. איך חוברו החלקים יחד? כשפרסמתי את החידה הקטנה הזו בעיתון לונדוני קיבלתי (אם כי הם היו לא מוזמנים) די הרבה דגמים, מעץ אלון, מעץ טיק, מהגוני, רוזווד, עץ סאטן, עץ תְרֵשָׁה ועץ אורן; חלקם באורך של חצי רגל, ואחרים בגדלים שונים ממש עד לדגם קטן ועדין בגודל של כחצי אינץ' מרובע. נראה שזה עורר עניין רב. מקורות:

  • שאלה

    נגיד ששתי פירמידות משיקות זו לזו אם אין להן נקודות פנימיות משותפות והן נחתכות במצולע מישורי לא מנוון. האם ייתכן ש 8 פירמידות במרחב ישיקו כולם אחת לשנייה? 
    א. אנג'אנס 

    מקורות: