קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
שאלה
שבעה סמוראים נלחמים זה בזה. כאשר סמוראי נפגע שלוש פעמים, הוא מת, ולא ניתן לפגוע בו יותר. ייתכן כי שני סמוראים יפגעו זה בזה בו זמנית. נתון כי כמות הפגיעות הכוללת שהנחית כל סמוראי שונה מהכמות שהנחית כל סמוראי אחר.
מקורות:
כמה סמוראים עלולים להיהרג בקרב? מצא את כל התשובות האפשריות. -
שאלה
מסביב לשולחן עגול יושבים לפחות שלושה אנשים, מתוכם t דוברי אמת ו- f שקרנים.
מקורות:
דוברי אמת תמיד אומרים אמת, שקרנים תמיד משקרים.
כל אחד מהם טוען, ששני השכנים שלו הם מאותו סוג. מה יכול להיות ערך היחס `f/t`?
עליך למצוא את כל התשובות האפשריות. -
שאלה
על דף לבן ציירו משושה קמור ומחומש קמור. מהו המספר הגדול ביותר של חלקים שאליהם הקווים
מקורות:
בציור יכולים לחלק את הדף? -
שאלה
נתון לוח בגודל 10×10. איילה רוצה לצבוע את משבצות הלוח בכחול ולבן (כל משבצת בצבע מסוים),
מקורות:
כך שבכל ריבוע שמורכב מ-4 משבצות יהיו בדיוק שתי משבצות לבנות ושתי משבצות כחולות. בכמה
דרכים שונות יכולה איילה לצבוע את המשבצות בהתאם לכללים האלה? -
שאלה
בכמה דרכים שונות ניתן לבחור 6 ספרות a,b,c,d,e,f שכולן שונות מ-0 (ולא בהכרח שונות זו
מזו), כך שהמספר השש-ספרתי `ab00cd` יתחלק במספר השש-ספרתי `cd00ef`? מקורות: -
שאלה
מספר N יקרא מוצלח אם הוא מקיים את שני התנאים הבאים:
* N הוא מספר חיובי שלם שמתחלק ב-101,
* ברישום של N מופיעות בדיוק שתי ספרות לא אפסיות.
למשל המספר 2020 הוא מוצלח, ואילו המספר 12120 אינו מוצלח כי יש בו 4 ספרות לא אפסיות.
מצאו את כמות המספרים המוצלחים שקטנים מ- `10^40`. מקורות: -
חידת כרטיס הנסיעה
כאשר הכרזות הגדולות והלוהטות הוצגו בתחנת הרכבת המחוזית הקטנה, והודיעו שהחברה הגדולה —— תפעיל רכבות נסיעה זולות ללונדון לחופשת חג המולד, תושבי Mudley-cum-Turmits היו בהתרגשות רבה. חצי שעה לפני שהרכבת הגיעה, משרד הכרטיסים הקטן היה צפוף בנוסעים כפריים, כולם נחושים לבקר את חבריהם במטרופולין הגדולה. פקיד הכרטוס לא היה רגיל להתמודד עם קהל ממדים כאלה, והוא סיפר לי אחר כך, תוך שהוא מנגב את מצחו הגברי, שמה שגרם לו לכל כך הרבה צרות היה העובדה שהכפריים האלה שילמו את דמי הנסיעה שלהם בהרבה מאוד כסף קטן.
הוא אמר שהיו לו מספיק רבעי פרוטה כדי לספק לחנות בגדים בווסט אנד עודף לשבוע, ומספר מספיק של מטבעות של שלושה פני עבור קהילות של שלוש כנסיות קהילתיות. "דמי הנסיעה האלה," אמר, "הם תשעה עשר שילינג ותשעה פני, ואני רוצה לדעת בכמה דרכים שונות אפשר לשלם סכום כזה במטבע הנוכחי של הממלכה הזו."
הנה, אם כן, חידה: בכמה דרכים שונות ניתן לשלם תשעה עשר שילינג ותשעה פני במטבע הנוכחי שלנו? זכרו שמטבע של ארבעה פני אינו בתוקף כעת.
מקורות:נושאים:קומבינטוריקה -
חידה בהיפוכים
רוב האנשים יודעים שאם לוקחים סכום כסף כלשהו בלירות, שילינגים ופני, שבו מספר הלירות (פחות מ-£`12`) עולה על מספר הפני, הופכים אותו (קוראים ללירות פני ולפני לירות), מוצאים את ההפרש, ואז הופכים ומוסיפים את ההפרש הזה, התוצאה היא תמיד £`12, 18`s. `11`d. אבל אם נשמיט את התנאי, "פחות מ-£`12`", וניתן לאפס לייצג שילינגים או פני—(`1`) מהו הסכום הנמוך ביותר שעליו הכלל לא יחול? (`2`) מהו הסכום הגבוה ביותר שעליו הוא יחול? כמובן, כאשר הופכים סכום כזה כמו £`14, 15`s. `3`d., ניתן לכתוב אותו £`3, 16`s. `2`d., שהוא זהה ל-£`3, 15`s. `14`d. מקורות: -
ספרות וריבועים
 ניתן לראות בתרשים שסידרנו את תשע הספרות בריבוע כך שהמספר בשורה השנייה גדול פי שניים מהמספר בשורה הראשונה, והמספר בשורה התחתונה גדול פי שלושה מהמספר בשורה העליונה. ישנן שלוש דרכים נוספות לסדר את הספרות כך שיתקבל אותו פתרון. האם תוכלו למצוא אותן?
מקורות:נושאים:אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה קומבינטוריקה -> בדיקת מקרים -> תהליכים
ניתן לראות בתרשים שסידרנו את תשע הספרות בריבוע כך שהמספר בשורה השנייה גדול פי שניים מהמספר בשורה הראשונה, והמספר בשורה התחתונה גדול פי שלושה מהמספר בשורה העליונה. ישנן שלוש דרכים נוספות לסדר את הספרות כך שיתקבל אותו פתרון. האם תוכלו למצוא אותן?
מקורות:נושאים:אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה קומבינטוריקה -> בדיקת מקרים -> תהליכים -
חידת הלוקרים
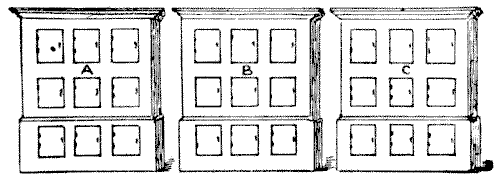
לאיש היו במשרדו שלושה ארונות, שבכל אחד מהם תשעה לוקרים, כפי שמוצג בדיאגרמה. הוא הורה לפקיד שלו להציב ספרה שונה על כל לוקר בארון A, ולעשות את אותו הדבר בארון B ובארון C. מכיוון שמותר לנו כאן לקרוא לאפס ספרה, ולא נאסר עליו להשתמש באפס כמספר, ברור שהייתה לו האפשרות להשמיט כל אחת מעשר הספרות מכל ארון.
כעת, המעסיק לא אמר שהלוקרים ימוספרו בסדר מספרי כלשהו, והוא הופתע לגלות, לאחר שהעבודה הסתיימה, שהספרות כנראה עורבבו באופן אקראי. כשקרא לפקיד שלו להסבר, הנער האקסצנטרי הצהיר שהעלתה בדעתו המחשבה לסדר את הספרות כך שבכל מקרה הן יצרו תרגיל חיבור פשוט, כאשר שתי השורות העליונות של הספרות יוצרות את הסכום בשורה התחתונה. אבל הנקודה המפתיעה ביותר הייתה זו: שהוא סידר אותן כך שהחיבור ב-A נתן את הסכום הקטן ביותר האפשרי, שהחיבור ב-C נתן את הסכום הגדול ביותר האפשרי, וכי כל תשע הספרות בסך הכל בשלושת הסכומים היו שונות. החידה היא להראות כיצד ניתן לעשות זאת. אין לאפשר עשרונים והאפס אינו יכול להופיע במקום המאות.
מקורות: