קומבינטוריקה, גאומטריה קומבינטורית

גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.

• טיול במישור

  נתונה במישור מערכת צירים x-y. יש להגיע מהנקודה (1,0) אל הנקודה (2006,2005), כאשר בכל מהלך מותר לנוע יחידה אחת מעלה (בכיוון החיובי של y) או יחידה אחת ימינה (בכיוון החיובי של ציר א).

  א. בכמה מסלולים שונים ניתן לבצע את המשימה?

  ב. בכמה מסלולים שונים ניתן לבצע את המשימה אם אסור באף שלב לעבור דרך נקודה הנמצאת על הישר x=y?

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> מקדמים בינומיים ומשולש פסקל גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> שיקוף
  מקורות:
  • תחרות גרוסמן, 2006 שאלה 7

• שאלה

  במעגל נמצאות 5778 נורות כבויות במרחקים קבועים. מתחת לכל נורה יש כפתור. כאשר לוחצים על הכפתור, זה משנה מצב של 4 נורות: הנורה שליד הכפתור, שתי נורות הבאות במעגל עם כיוון השעון, ואת הנורה הנגדית לכפתור (נורה כבויה נדלקת כאשר משנים את מצבה, ונורה דולקת נכבית). מהי הכמות המרבית של נורות שיכולות להיות דלוקות בו-זמנית?
  

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 8

• שאלה

  על דף לבן ציירו משושה קמור ומחומש קמור. מהו המספר הגדול ביותר של חלקים שאליהם הקווים
  בציור יכולים לחלק את הדף?

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשפ"ה, שלב ב שאלה 1

• החתולים של הקוסם

  קוסם הניח עשרה חתולים בתוך מעגל קסם כפי שמוצג באיור שלנו, והפנט אותם כך שיישארו נייחים במהלך רצונו. לאחר מכן הוא הציע לצייר שלושה מעגלים בתוך המעגל הגדול, כך שאף חתול לא יוכל להתקרב לחתול אחר מבלי לחצות מעגל קסם. נסו לצייר את שלושת המעגלים כך שלכל חתול תהיה מתחם משלו ולא יוכל להגיע לחתול אחר מבלי לחצות קו.
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור -> מעגלים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 167

• המלך והמבצרים

  היה היה, בעת העתיקה, מלך חזק, שהיו לו רעיונות מוזרים בנושא האדריכלות הצבאית. הוא טען שיש כוח וחיסכון גדולים בצורות סימטריות, ותמיד ציטט את דוגמת הדבורים, שבונות את החלות שלהן בתאים משושים מושלמים, כדי להוכיח שיש לו את הטבע שתומך בו. הוא החליט לבנות עשרה מבצרים חדשים במדינתו, שכולם יהיו מחוברים בחומות מבוצרות, שייצרו חמישה קווים עם ארבעה מבצרים בכל קו. האדריכל המלכותי הציג את תוכניתו המקדימה בצורה שהראיתי. אבל המלך הצביע על כך שניתן לגשת לכל מבצר מבחוץ, וציווה שהתוכנית תשונה כך שכמה שיותר מבצרים יהיו חופשיים מתקיפה מבחוץ, וניתן יהיה להגיע אליהם רק על ידי חציית החומות המבוצרות. האדריכל השיב שהוא חושב שאי אפשר לסדר אותם כך שאפילו מבצר אחד, שהמלך הציע להשתמש בו כמגורים מלכותיים, יהיה מוגן כל כך, אבל הוד מלכותו עד מהרה הבהיר לו כיצד ניתן לעשות זאת. איך הייתם בונים את עשרת המבצרים והביצורים כדי למלא בצורה הטובה ביותר את דרישות המלך? זכרו שהם חייבים ליצור חמישה קווים ישרים עם ארבעה מבצרים בכל קו.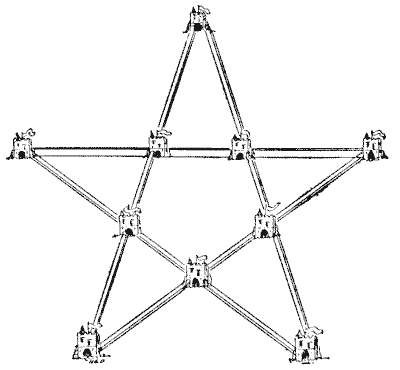
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 206

• דובדבנים ושזיפים

  האיור הוא תוכנית של קוטג' כפי שהוא עומד מוקף במטע של חמישים וחמישה עצים. עשרה מהעצים הללו הם דובדבנים, עשרה הם שזיפים, והשאר תפוחים. הדובדבנים נשתלו כך שייצרו חמישה קווים ישרים, עם ארבעה עצי דובדבן בכל קו. עצי השזיף נשתלו גם הם כך שייצרו חמישה קווים ישרים עם ארבעה עצי שזיף בכל קו. החידה היא להראות אילו הם עשרת עצי הדובדבן ואילו הם עשרת עצי השזיף. על מנת שלדובדבנים ולשזיפים יהיה את הנוף הטוב ביותר, כמה שפחות (בתנאים הקיימים) נשתלים בצד הצפוני והמזרחי של המטע. כמובן שבהוצאת קבוצה של עשרה עצים (דובדבן או שזיף, לפי העניין) מתעלמים מכל העצים המפרידים. זאת אומרת, ארבעה עצים יכולים להיות בקו ישר ללא קשר לעצים אחרים (או לבית) שנמצאים ביניהם. אחרי החידה האחרונה זה יהיה די קל.
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 207

• עשרים ואחד עצים

  אדון רצה לשתול עשרים ואחד עצים בפארק שלו כך שהם ייצרו שתים עשרה שורות ישרות עם חמישה עצים בכל שורה. האם הייתם יכולים לספק לו סידור סימטרי נאה שיעמוד בתנאים אלה?
  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 209

• תריסר פשטידות בשר

  ניתן לראות באיור שלנו כיצד ניתן להניח תריסר פשטידות בשר על השולחן כך שייצרו שש שורות ישרות עם ארבע פשטידות בכל שורה. החידה היא להסיר רק ארבע מהן למיקומים חדשים כך שיהיו שבע שורות ישרות עם ארבע בכל שורה. אילו ארבע הייתם מסירים, והיכן הייתם מחליפים אותן?
  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 211

• טורקים ורוסים

  חידה זו היא בסגנון בעיית האפרידי שפורסמה על ידי ב-Tit-Bits לפני כמה שנים.

  על שטח מישורי פתוח, קבוצת חיילי רגלים רוסים, שאף אחד מהם לא הוצב באותו מקום, הופתעה לפתע על ידי שלושים ושניים טורקים, שפתחו באש על הרוסים מכל הכיוונים. כל אחד מהטורקים ירה בו זמנית כדור, וכל כדור חלף מיד מעל ראשיהם של שלושה חיילים רוסים. מכיוון שכל אחד מהכדורים הללו הרג אדם אחר, החידה היא לגלות מהו המספר הקטן ביותר האפשרי של חיילים שהקבוצה הרוסית יכולה הייתה להכיל ומה היו האבדות בכל צד.

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 213

• תשעת השקדים

  "הנה חידה קטנה," אמר כומר, "שמצאתי אותה מרתקת במיוחד. היא כל כך פשוטה, ובכל זאת היא משאירה אותך מעוניין ללא הגבלת זמן."

  הכומר הנכבד לקח דף נייר וחילק אותו לעשרים וחמישה ריבועים, כמו חלק מרובע של לוח שחמט. אחר כך הניח תשעה שקדים על הריבועים המרכזיים, כפי שמוצג באיור, שם ייצגנו דלפקים ממוספרים לנוחיות במתן הפתרון.

  "עכשיו, החידה היא," המשיך הכומר, "להסיר שמונה מהשקדים ולהשאיר את התשיעי בריבוע המרכזי. אתה מבצע את ההסרות על ידי קפיצה של שקד אחד מעל שקד אחר לריבוע הריק שמעבר והסרת זה שקפצו מעליו—בדיוק כמו בדמקה, רק כאן אתה יכול לקפוץ לכל כיוון, ולא רק באלכסון. העניין הוא לעשות את זה במספר המהלכים המועט ביותר האפשרי."

  ניסיון הדגמה הבא יבהיר הכל. קפוץ `4` מעל `1, 5` מעל `9, 3` מעל `6, 5` מעל `3, 7` מעל `5` ו-`2, 4` מעל `7, 8` מעל `4`. אבל `8` לא נשאר בריבוע המרכזי, כפי שהוא צריך להיות. זכור להסיר את אלה שאתה קופץ מעליהם. כל מספר של קפיצות ברציפות עם אותו שקד נחשב למהלך אחד.

  

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית חידות ורבוסים
  מקורות: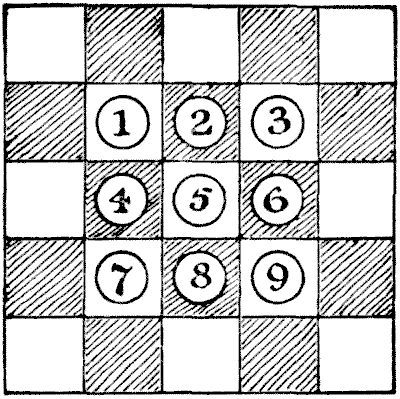
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 229