קומבינטוריקה, גאומטריה קומבינטורית

גאומטריה קומבינטורית בוחנת את הקשרים בין קומבינטוריקה לגאומטריה. היא עוסקת בבעיות על סידורים, תצורות ותכונות של אובייקטים גאומטריים בדידים (נקודות, קווים, מצולעים). שאלות כוללות לעיתים קרובות ספירה, הוכחות קיום ואי-שוויונים גאומטריים.

חתכו צורה גאומטריה על נייר משבצות

  • הזבוב על האוקטהדרון

    "תראה," אמר הפרופסור לעמיתו, "אני צופה בזבוב הזה על האוקטהדרון, והוא מגביל את הליכותיו אך ורק לקצוות. מה יכולה להיות הסיבה שלו להימנע מהצדדים?"

    "אולי הוא מנסה לפתור איזושהי בעיית מסלול," הציע השני. "בהנחה שהוא מתחיל מנקודת העליונה, כמה מסלולים שונים יש שבהם הוא יכול ללכת על כל הקצוות, מבלי ללכת פעמיים לאורך אותו קצה בכל מסלול?"

     

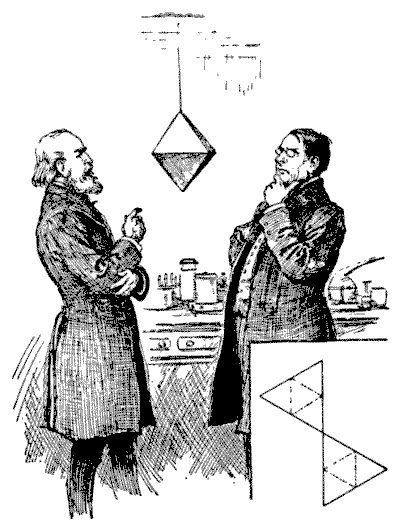
    הבעיה הייתה קשה יותר ממה שהם ציפו, ולאחר שעבדו עליה ברגעי הפנאי במשך מספר ימים התוצאות שלהם לא הסכימו — למעשה, שניהם טעו. אם הקורא מופתע מכישלונם, שינסה בעצמו את החידה הקטנה. אסביר רק שהאוקטהדרון הוא אחד מחמשת הגופים הרגילים, או האפלטוניים, והוא תחום תחת שמונה משולשים שווים ושווי צלעות. אם תגזור את שני חלקי הקרטון בצורה המוצגת בשולי האיור, תגזור חצי דרך לאורך הקווים המקווקווים ואז תכופף אותם ותחבר אותם, תקבל אוקטהדרון מושלם. בכל מסלול על פני כל הקצוות יתגלה שהזבוב חייב להסתיים בנקודת המוצא בראש.

    מקורות:

  • הפאזל של האיקוסהדרון

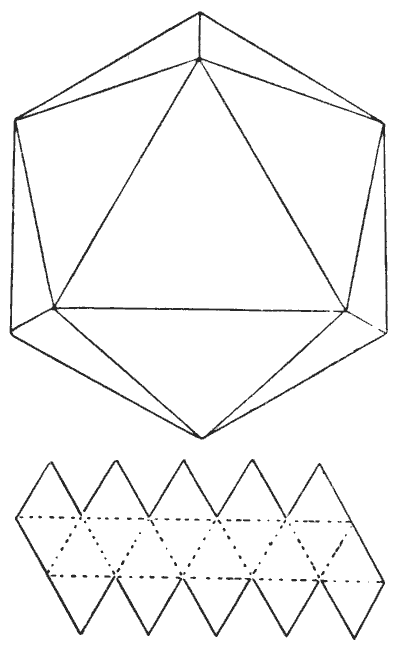
    האיקוסהדרון הוא עוד אחד מחמשת הגופים הרגילים, או האפלטוניים, שכל צדדיהם, זוויותיהם ומישוריהם דומים ושווים. הוא תחום על ידי עשרים משולשים שווי צלעות דומים. אם תגזרו חתיכת קרטון בצורה המוצגת בדיאגרמה הקטנה יותר, ותחתכו חצי עובי לאורך הקווים המקווקווים, היא תתקפל ותיצור איקוסהדרון מושלם.

    ובכן, גוף אפלטוני לא בהכרח מציין גוף שמימי; אבל זה יתאים למטרת הפאזל שלנו אם נניח שיש כוכב לכת ראוי למגורים בצורה הזו. נניח גם שבשל שפע מים, היבשה היחידה נמצאת לאורך הקצוות, ושלתושבים אין ידע בניווט. אם כל אחד מהקצוות האלה באורך `10,000` מיילים, ומטייל בודד ממוקם בקוטב הצפוני (הנקודה הגבוהה ביותר המוצגת), כמה רחוק הוא יצטרך לנסוע לפני שהוא יבקר בכל חלק ראוי למגורים בכוכב הלכת — כלומר, יחצה כל אחד מהקצוות?

    מקורות:

  • הטיול הגדול

    אחת החידות היומיומיות של החיים היא תכנון מסלולים. אם אתם יוצאים לחופשה על אופניים, או לטיול מוטורי, תמיד עולה השאלה כיצד לנצל את הזמן והמשאבים שלכם בצורה הטובה ביותר. החלטתם להגיע למקום מסוים, לכלול ביקורים בעיר כזו וכזו, לנסות לראות משהו מעניין במיוחד במקום אחר, ואולי לנסות לבקר חבר ותיק בנקודה שלא תוציא אתכם בהרבה מהדרך. אז אתם צריכים לתכנן את המסלול שלכם כדי להימנע מכבישים גרועים, אזורים לא מעניינים, ואם אפשר, מהצורך לחזור באותה דרך שבה נסעתם. עם מפה לפניכם, ניגשים לפתרון החידה המעניינת. אציג לכם שאלה קטנה המבוססת על קווים אלה.

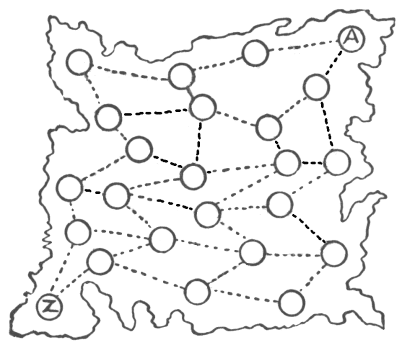
    אני מציג מפה גסה של מדינה—אין צורך לומר איזו מדינה—העיגולים מייצגים ערים והקווים המקווקווים את מסילות הברזל המחברות ביניהן. עכשיו, בעיר המסומנת A חי אדם שנולד שם, ובמשך כל חייו מעולם לא עזב את מקום הולדתו. מנעוריו הוא היה חרוץ מאוד, דבק בעקביות במקצועו, ולא היה לו רצון לשוטט בחוץ. עם זאת, בהגיעו לגיל חמישים הוא החליט לראות קצת מהמדינה שלו, ובמיוחד לבקר חבר ותיק מאוד שגר בעיר המסומנת Z. מה שהוא הציע היה כזה: שהוא יתחיל מביתו, ייכנס לכל עיר פעם אחת בלבד, ויסיים את מסעו ב-Z. מכיוון שהוא החליט לבצע את הטיול הגדול הזה ברכבת בלבד, הוא התקשה קצת לתכנן את המסלול שלו, אבל בסופו של דבר הוא הצליח לעשות זאת. איך הוא הצליח? אל תשכחו שצריך לבקר בכל עיר פעם אחת, ולא יותר מפעם אחת.

    מקורות:

  • רצים - שמורים

    כמה רצים נחוצים כדי שכל משבצת תהיה מאויישת או מותקפת, וכל רץ יהיה שמור על ידי רץ אחר? ואיך ניתן למקם אותם? מקורות:

  • בעיה בפסיפסים

    אמנות יצירת תמונות או עיצובים באמצעות חיבור חתיכות של חומרים קשים, צבועים באופן טבעי או מלאכותי, היא עתיקה מאוד. היא הייתה ידועה בוודאות בתקופת הפרעונים, ואנו מוצאים התייחסות במגילת אסתר ל"מרצפת בהט ושש ודר וסחרת". נראה כי חלק מהעבודה העתיקה הזו שהגיעה אלינו, במיוחד כמה מהפסיפסים הרומיים, מראים בבירור, גם כאשר העיצוב אינו ניכר בתחילה, כי מחשבה רבה הושקעה בסידורים שנראים לכאורה לא מסודרים. כאשר, למשל, העבודה הופקה עם מספר מוגבל מאוד של צבעים, ישנן עדויות לתחכום רב במניעת גוונים זהים המגיעים בסמיכות זה לזה. קוראות ליידי שמכירות את בניית שמיכות טלאים ידעו כמה רצוי לפעמים, כאשר הן מוגבלות בבחירת החומר, למנוע מחתיכות מאותו חומר להתקרב מדי זו לזו. כעת, החידה הזו תחול במידה שווה על שמיכות טלאים או ריצוף טסלטה.

    ניתן לראות מהדיאגרמה כיצד ניתן לרצף פיסת רצפה מרובעת עם שישים ושתיים אריחים מרובעים משמונת הצבעים סגול, אדום, צהוב, ירוק, כתום, ארגמן, לבן וכחול (המצוינים באותיות הראשונות), כך שאף אריח אינו נמצא בקו אחד עם אריח צבעוני דומה, אנכית, אופקית או אלכסונית. לא ניתן יהיה להציב שישים וארבעה אריחים כאלה בתנאים אלה, אך שני הריבועים המוצלים תפוסים על ידי פתחי אוורור מברזל.

     

    החידה היא זו. יש להסיר את שני פתחי האוורור הללו למיקומים המצוינים על ידי האריחים התחומים כהה, ושני אריחים ממוקמים בריבועי הפינה התחתונה הללו. האם אתה יכול להתאים מחדש את שלושים ושניים האריחים כך ששניים מאותו צבע עדיין לא יהיו בקו?

    מקורות:

  • שומרי האבירים

     

    האביר הוא הקומיקאי הנמוך חסר האחריות של לוח השחמט. "הוא נוכל מאוד לא בטוח, מתגנב ומדכא," אומר סופר אמריקאי. "הוא יכול לזוז רק שני ריבועים, אך מפצה על כמות התנועה שלו באיכותה, שכן הוא יכול לקפוץ ריבוע אחד הצידה ואחד קדימה בו זמנית, כמו חתול; יכול לעמוד על רגל אחת באמצע הלוח ולקפוץ לכל אחד משמונת הריבועים שהוא בוחר; יכול לעלות על צד אחד של גדר ולהשמיץ שלושה או ארבעה אנשים בצד השני; יש לו דרך מעוררת התנגדות להכניס את עצמו למקומות בטוחים שבהם הוא יכול להפחיד את המלך ולאלץ אותו לזוז, ואז לטרוף מלכה. לרוע טהור אין לאביר שווה, וכאשר אתה רודף אחריו מחור אחד הוא קופץ לאחר." נעשו ניסיונות שוב ושוב להשיג הגדרה קצרה, פשוטה ומדויקת של תנועת האביר—ללא הצלחה. זה באמת מורכב מלהזיז ריבוע אחד כמו צריח, ואז ריבוע אחר כמו רץ—שני הפעולות נעשות בקפיצה אחת, כך שלא משנה אם הריבוע הראשון שעוברים עליו תפוס על ידי כלי אחר או לא. זו, למעשה, התנועה הקופצת היחידה בשחמט. אבל קשה ככל שיהיה להגדיר, ילד יכול ללמוד את זה על ידי הסתכלות תוך מספר דקות.

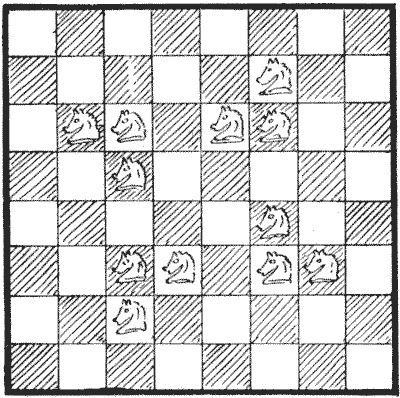
    הראיתי בתרשים כיצד ניתן להציב שנים עשר אבירים (המספר הקטן ביותר האפשרי שיבצע את המשימה) על לוח השחמט כך שכל ריבוע יהיה או תפוס או מותקף על ידי אביר. בחן כל ריבוע בתורו, ותגלו שזה כך. כעת, החידה במקרה זה היא לגלות מהו המספר הקטן ביותר האפשרי של אבירים הנדרש כדי שכל ריבוע יהיה או תפוס או מותקף, וכל אביר מוגן על ידי אביר אחר. ואיך הייתם מסדרים אותם? יתברר שמתוך שנים עשר המוצגים בתרשים רק ארבעה מוגנים כך על ידי היותם במרחק מהלך של אביר מאביר אחר.

    מקורות:

  • העלמה הדועכת

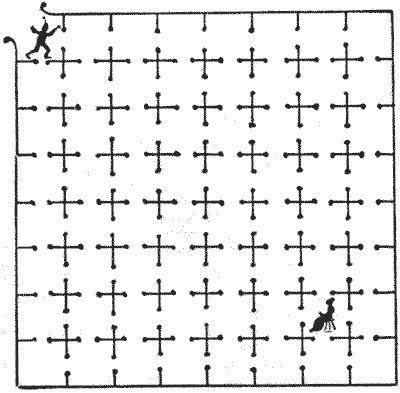    ברון מרושע בימים הטובים של פעם כלא עלמה חפה מפשע באחד הצינוקים העמוקים ביותר מתחת לחפיר הטירה. ניתן לראות מהאיור שלנו שהיו שישים ושלושה תאים בצינוק, כולם מחוברים בדלתות פתוחות, והעלמה הייתה כבולה בתא שבו היא מוצגת. כעת, אביר אמיץ, שאהב את העלמה, הצליח להציל אותה מהאויב. לאחר שהשיג כניסה לצינוק בנקודה שבה הוא נראה, הוא הצליח להגיע לעלמה לאחר שנכנס לכל תא פעם אחת בלבד. קחו את העיפרון שלכם ונסו להתחקות אחר מסלול כזה. לאחר שהצלחתם, נסו לגלות מסלול בעשרים ושניים נתיבים ישרים דרך התאים. ניתן לעשות זאת במספר הזה מבלי להיכנס לאף תא פעם שנייה. מקורות:

  • החידה החדשה של הרץ

     

    זוהי חידה קטנה ומסקרנת למדי. הניחו שמונה רצים (ארבעה שחורים וארבעה לבנים) על לוח השחמט המצומצם, כפי שמוצג באיור. הבעיה היא לגרום לרצים השחורים להחליף מקומות עם הלבנים, כך שאף רץ לא יתקוף רץ אחר מצבע מנוגד. הם חייבים לנוע לחלופין—תחילה רץ לבן, אחר כך רץ שחור, אחר כך רץ לבן, וכן הלאה. כאשר תצליחו לעשות זאת בכלל, נסו למצוא את מספר המהלכים המינימלי האפשרי.

    אם תוציאו את הרצים שעומדים על משבצות שחורות, ותשחקו רק על המשבצות הלבנות, תגלו שהחידה האחרונה שלי הסתובבה על צידה.

    מקורות:

  • סיור המלכה

    החידה של ביצוע סיור שלם בלוח השחמט עם המלכה במספר המהלכים המועט ביותר האפשרי (שבו ניתן לבקר בריבועים יותר מפעם אחת) ניתנה לראשונה על ידי סם לויד המנוח ב-אסטרטגיית שחמט שלו. אבל הפתרון המוצג להלן הוא זה שהוא נתן ב-אגוזי שחמט אמריקאים ב-`1868`. תיעדתי לפחות שישה פתרונות שונים במספר המינימלי של מהלכים - ארבעה עשר - אבל זה הטוב מכולם, מסיבות שאסביר.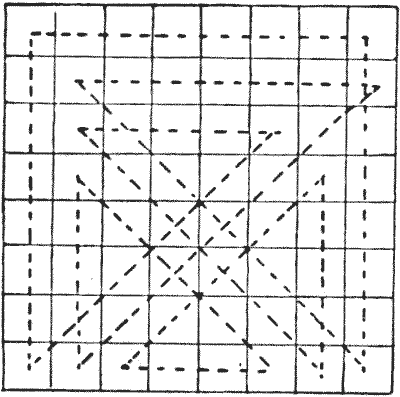 אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: - 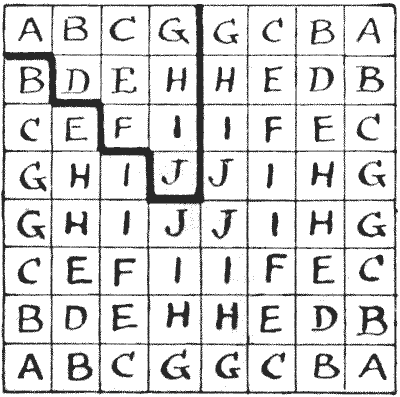התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה. מקורות:

  • פאזל הכוכבים

     

    הניחו את חוד העיפרון שלכם על אחד הכוכבים הלבנים ו(מבלי להרים את העיפרון מהדף) מחקו את כל הכוכבים בארבעה עשר קווים ישרים רציפים, כשאתם מסיימים בכוכב הלבן השני. הקווים הישרים שלכם יכולים להיות בכל כיוון שתרצו, רק כל פנייה חייבת להתבצע על כוכב. אין התנגדות למחוק כוכב כלשהו יותר מפעם אחת.

    במקרה הזה, כאשר ריבועי ההתחלה והסיום שלכם מקובעים בצורה לא נוחה, אינכם יכולים להשיג פתרון על ידי שבירת מסע מלכה, או בכל דרך אחרת באמצעות מסעי מלכה בלבד. אבל מותר לכם להשתמש בקווים ישרים אלכסוניים —כגון מהכוכב הלבן העליון ישירות לכוכב פינתי.

    מקורות: