גאומטריה, גאומטריה במישור

גאומטריה במישור עוסקת בצורות וגופים על משטח שטוח ודו-ממדי. היא מכסה תכונות של נקודות, קווים, זוויות, מצולעים (כמו משולשים ומרובעים) ומעגלים. שאלות כוללות בדרך כלל הוכחות, בנייה וחישובים הקשורים לאלמנטים אלו.

חשבון שטחים משולשים מעגלים סימטריה חשבון זוויות משפט פיתגורס אי שוויון המשולש

• שאלה

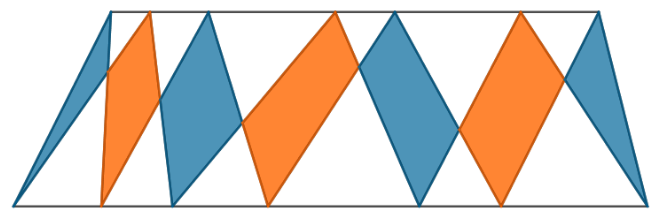
  בציור מצויר טרפז, שעל כל בסיס שלו נבחרו 5 נקודות. חלק מהנקודות חוברו על ידי קטעים ישרים. הראו כי סכום השטחים הכחולים שווה לסכום השטחים הכתומים.
  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים
  מקורות:
  • אולימפיאדת בנו ארבל, 2019, כיתה ח שאלה 5

• שאלה

  נתון משולש ABC ומעגל עם רדיוס 10 שחותך כל אחד מהצלעות של המשולש בשתי נקודות: נקודות
  P ו-Q על הצלע BC, נקודות K ו-L על הצלע CA, ונקודות M ו-N על הצלע AB, כך שמתקיים `AM = MN = KL = PQ = 2PB = BC/6`. מצאו את שטח המשולש ABC.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> מעגלים
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשפ"ה, שלב ב שאלה 6

• שלושת הכפרים

  יצאתי לדרך אתמול כדי לנסוע במכונית מאייקריפילד לבאטרפורד, אבל בטעות לקחתי את הכביש שעובר דרך צ'יזברי, אשר קרוב יותר לאייקריפילד מאשר לבאטרפורד, והוא שנים עשר מיילים משמאל לכביש הישיר שהייתי צריך לנסוע בו. לאחר שהגעתי לבאטרפורד גיליתי שעברתי שלושים וחמישה מיילים. מהם שלושת המרחקים בין הכפרים הללו, כאשר כל אחד מהם הוא מספר שלם של מיילים? אוסיף ואציין ששלושת הכבישים ישרים לחלוטין.
  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים אלגברה -> בעיות מילוליות גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 69

• הצלב והמשולש

  חתוך צלב יווני לשישה חלקים שייצרו משולש שווה צלעות. זוהי בעיה קשה נוספת, ואציין כאן שפתרון מעשי בלתי אפשרי ללא ידע מוקדם בשיטה שלי להמרת משולש שווה צלעות לריבוע (ראה מס' `26`, "חידות קנטרברי").
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 144

• המשולש המנותח

   

  חידה טובה היא זו שהג'נטלמן באיור מציג לחבריו. הוא פשוט גזר מנייר משולש שווה צלעות — כלומר, משולש שבו שלוש הצלעות באותו אורך. הוא מציע לחתוך אותו לחמישה חלקים בצורה כזו שהם יתאימו זה לזה וייצרו שניים או שלושה משולשים שווי צלעות קטנים יותר, תוך שימוש בכל החומר בכל מקרה. האם תוכלו לגלות כיצד יש לבצע את החיתוכים?

  זכרו שכאשר הכנתם את חמשת החלקים שלכם, עליכם להיות מסוגלים, כרצוי, לחבר אותם יחד כדי ליצור או את המשולש המקורי הבודד או ליצור שני משולשים או ליצור שלושה משולשים — כולם שווי צלעות.

  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 156

• שלוש תחנות רכבת

  כששבתי בקרון רכבת, הבחנתי בקצה השני של הקרון באדון מכובד, שהכרתי למראה, משוחח עם נוסע אחר, שהיה ככל הנראה חבר שלו.

  "כמה רחוק אתה צריך לנסוע אל מקומך מתחנת הרכבת?" שאל הזר.

  "ובכן," השיב האדון, "אם ארד באפלפורד, זה בדיוק אותו מרחק כמו אם אסע לברידג'פילד, עוד חמישה עשר מיילים הלאה; ואם אחליף רכבת באפלפורד ואסע משם שלושה עשר מיילים לקרטרטון, זה עדיין יהיה אותו מרחק. אתה רואה, אני נמצא במרחק שווה משלוש התחנות, אז יש לי מבחר טוב של רכבות."

  ידעתי שבדיוק ברידג'פילד נמצאת במרחק של ארבעה עשר מיילים מקרטרטון, אז שעשעתי את עצמי בחישוב המרחק המדויק שהאדון צריך לנסוע הביתה, לא משנה באיזו תחנה הוא ירד. מה היה המרחק?

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים אלגברה -> בעיות מילוליות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 181

• אחוזות יורקשייר

   

  ביקרתי באחת הערים הגדולות של יורקשייר. בדרכי לתחנת הרכבת ביום עזיבתי, אדם דחף לי עלון, לקחתי אותו לקרון הרכבת וקראתי אותו בשעות הפנאי שלי. הוא הודיע לי ששלוש אחוזות שכנות ביורקשייר מוצעות למכירה. כל אחוזה הייתה בצורת ריבוע, והן הצטרפו זו לזו בפינותיהן, בדיוק כפי שמוצג בתרשים. אחוזה A מכילה בדיוק `370` אקרים, B מכילה `116` אקרים, ו-C `74` אקרים.

  כעת, פיסת הקרקע המשולשת הקטנה התחומה על ידי שלוש האחוזות הריבועיות לא הוצעה למכירה, ומסיבה לא מיוחדת, התעוררתי לסקרנות לגבי שטח החלקה הזו. כמה אקרים היא הכילה?

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 189

• האחוזה של החוואי וורצל

   

  אציג כעת בעיית שטח נוספת. ההדגמה של התשובה שאציג, אני חושב, תימצא גם מעניינת וגם קלה להבנה.

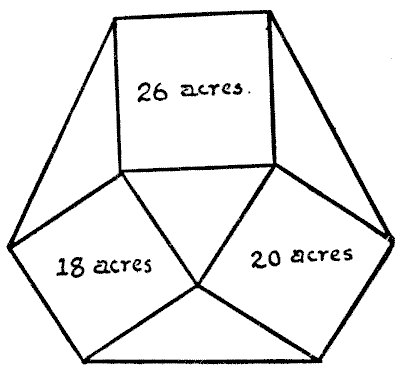
  החוואי וורצל היה הבעלים של שלושה שדות מרובעים כפי שמוצג בתוכנית המצורפת, המכילים בהתאמה `18, 20`, ו-`26` אקרים. כדי להקיף את רכושו בגדר טבעת, הוא קנה את ארבעת השדות המשולשים המפרידים. החידה היא לגלות מה היה אז השטח הכולל של האחוזה שלו.

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 190

• העז הקשורה

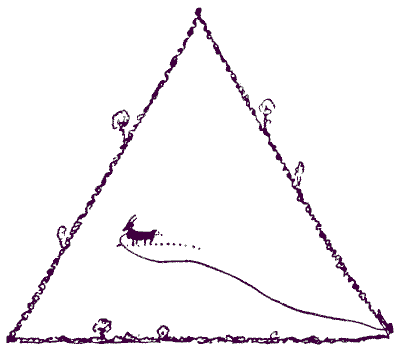  הנה בעיה קטנה שכל אחד צריך לדעת איך לפתור. העז ממוקמת באחו בשטח של חצי אקר, אשר צורתו משולש שווה צלעות. היא קשורה לעמוד בפינה אחת של השדה. מה צריך להיות אורך החבל (באינץ' הקרוב ביותר) כדי שהעז תוכל לאכול רק חצי מהדשא בשדה? ההנחה היא שהעז יכולה לאכול עד סוף החבל.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> חשבון זוויות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 196

• החידה של פאפוס

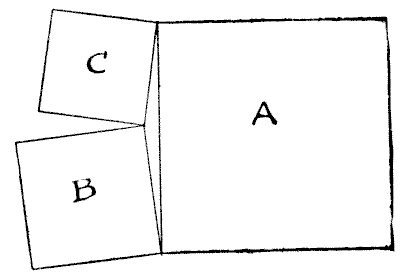
  זוהי חידה מאת פאפוס, שחי באלכסנדריה בערך בסוף המאה השלישית. זהו המשפט החמישי בספר השמיני של אוספים מתמטיים שלו. אני מציג אותה בצורה שהצגתי אותה לפני כמה שנים תחת הכותרת "החידה של פאפוס", רק כדי לראות כמה קוראים יגלו שהיא מאת פאפוס עצמו. "לאבא של העלמה הקטנה יש שני פיסות קרטון מלבניות בגדלים שונים, והוא גזר פיסה משולשת מאחת מהן, כך שכאשר היא תלויה בחוט מהנקודה A היא תלויה כשהצד הארוך אופקי לחלוטין, כפי שמוצג באיור. הוא הדהים את הילדה בכך שביקש ממנה למצוא את הנקודה A על הכרטיס השני, כדי להפיק תוצאה דומה כאשר הוא נחתך ותלוי בחוט." כמובן, אסור למצוא את הנקודה על ידי גזירות ניסיון. נקודה מוזרה ויפה מעורבת בהצגת החידה הזו. האם הקורא יכול לגלות אותה?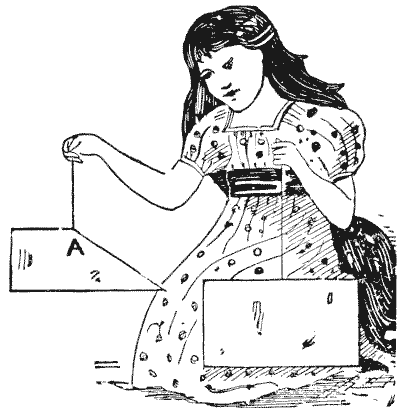
  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 199