גאומטריה, גאומטריה במישור
גאומטריה במישור עוסקת בצורות וגופים על משטח שטוח ודו-ממדי. היא מכסה תכונות של נקודות, קווים, זוויות, מצולעים (כמו משולשים ומרובעים) ומעגלים. שאלות כוללות בדרך כלל הוכחות, בנייה וחישובים הקשורים לאלמנטים אלו.
חשבון שטחים משולשים מעגלים סימטריה חשבון זוויות משפט פיתגורס אי שוויון המשולש-
חידת לינולאום נוספת
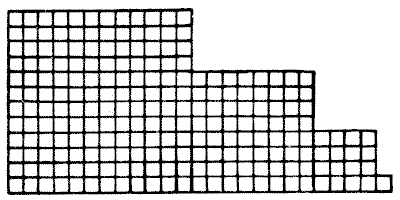
האם תוכלו לחתוך את פיסת הלינולאום הזו לארבע חתיכות שיתאימו זו לזו וייצרו ריבוע מושלם? כמובן שהחיתוכים יכולים להתבצע רק לאורך הקווים.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 177
-
ארבעת הבנים
קוראים יזהו את הדיאגרמה כחבר ותיק מימי נעוריהם. לאיש הייתה אחוזה בצורת ריבוע. הוא הוריש לאלמנתו את הרבע המוצל של האחוזה. את היתר היה צריך לחלק באופן שווה בין ארבעת בניו, כך שכל אחד יקבל קרקע באותו שטח בדיוק ובאותה צורה בדיוק. מוצג לנו איך זה נעשה. אבל המשך הסיפור אינו ידוע כל כך. במרכז האחוזה הייתה באר, המסומנת על ידי הנקודה הכהה, ובנימין, צ'ארלס ודוד התלוננו שהחלוקה אינה "הוגנת", מכיוון שלאAlfred הייתה גישה לבאר הזו, בעוד שהם לא יכלו להגיע אליה מבלי להסיג את גבולו של מישהו אחר. החידה היא להראות כיצד יש לחלק את האחוזה כך שלכל בן תהיה קרקע באותו צורה ובאותו שטח, ולכל אחד תהיה גישה לבאר מבלי לרדת מהשטח שלו.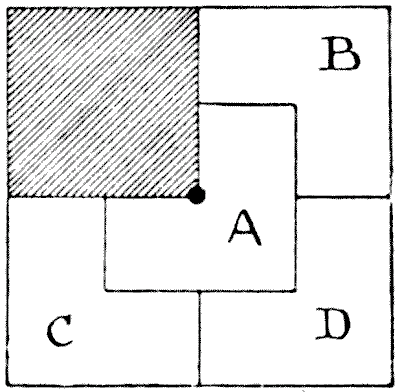 מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 180
-
חידת חבל הכביסה
ילד קשר חבל כביסה מראש כל אחד משני עמודים לבסיס של השני. לאחר מכן הוא הציע לאביו את השאלה הבאה. אם עמוד אחד היה בדיוק שבעה רגל מעל הקרקע והשני בדיוק חמישה רגל, מה היה הגובה מהקרקע שבו שני החבלים הצטלבו זה בזה? מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 186
-
הגן של ליידי בלינדה
ליידי בלינדה היא גננת נלהבת. באיור היא מתוארת כשהיא שקועה בפתרון בעיה קטנה ומהנה שאותה אספר. אחד הגנים שלה הוא בצורת מלבן, מוקף בגדר חיה גבוהה של צמח ההולי, והיא הופכת אותו לגינת ורדים לטיפוח כמה מזני הורדים המשובחים ביותר שלה. היא רוצה להקדיש בדיוק מחצית משטח הגן לפרחים, בערוגה גדולה אחת, ואת המחצית השנייה לשביל המקיף אותו מכל צדדיו ברוחב שווה. גן כזה מוצג בתרשים בתחתית התמונה. כיצד עליה לסמן את הגן בתנאים פשוטים אלה? יש לה רק סרט מדידה, באורך הגן, כדי לעשות זאת, ומכיוון שגדר ההולי עבה וצפופה מאוד, עליה לבצע את כל המדידות בפנים. ליידי בלינדה לא ידעה את המידות המדויקות של הגן, ומכיוון שלא היה צורך שתדע, גם אני לא מציין מידות. זו משימה פשוטה למדי, לא משנה מה גודל או פרופורציות הגן. עם זאת, כמה גננות היו יודעות בדיוק כיצד להמשיך? סרט המדידה יכול להיות פשוט למדי - כלומר, אין צורך שיהיה מדד מדורג. מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים אלגברה -> טכניקה אלגברית אלגברה -> משוואות
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים אלגברה -> טכניקה אלגברית אלגברה -> משוואות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 195
-
המלך והמבצרים
היה היה, בעת העתיקה, מלך חזק, שהיו לו רעיונות מוזרים בנושא האדריכלות הצבאית. הוא טען שיש כוח וחיסכון גדולים בצורות סימטריות, ותמיד ציטט את דוגמת הדבורים, שבונות את החלות שלהן בתאים משושים מושלמים, כדי להוכיח שיש לו את הטבע שתומך בו. הוא החליט לבנות עשרה מבצרים חדשים במדינתו, שכולם יהיו מחוברים בחומות מבוצרות, שייצרו חמישה קווים עם ארבעה מבצרים בכל קו. האדריכל המלכותי הציג את תוכניתו המקדימה בצורה שהראיתי. אבל המלך הצביע על כך שניתן לגשת לכל מבצר מבחוץ, וציווה שהתוכנית תשונה כך שכמה שיותר מבצרים יהיו חופשיים מתקיפה מבחוץ, וניתן יהיה להגיע אליהם רק על ידי חציית החומות המבוצרות. האדריכל השיב שהוא חושב שאי אפשר לסדר אותם כך שאפילו מבצר אחד, שהמלך הציע להשתמש בו כמגורים מלכותיים, יהיה מוגן כל כך, אבל הוד מלכותו עד מהרה הבהיר לו כיצד ניתן לעשות זאת. איך הייתם בונים את עשרת המבצרים והביצורים כדי למלא בצורה הטובה ביותר את דרישות המלך? זכרו שהם חייבים ליצור חמישה קווים ישרים עם ארבעה מבצרים בכל קו.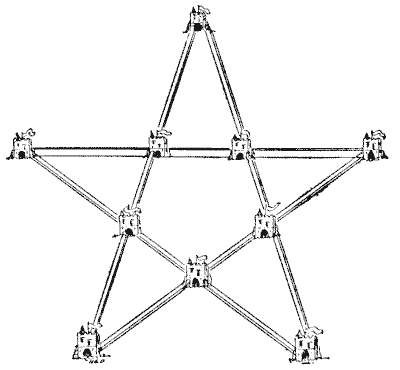 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 206
-
דובדבנים ושזיפים
 האיור הוא תוכנית של קוטג' כפי שהוא עומד מוקף במטע של חמישים וחמישה עצים. עשרה מהעצים הללו הם דובדבנים, עשרה הם שזיפים, והשאר תפוחים. הדובדבנים נשתלו כך שייצרו חמישה קווים ישרים, עם ארבעה עצי דובדבן בכל קו. עצי השזיף נשתלו גם הם כך שייצרו חמישה קווים ישרים עם ארבעה עצי שזיף בכל קו. החידה היא להראות אילו הם עשרת עצי הדובדבן ואילו הם עשרת עצי השזיף. על מנת שלדובדבנים ולשזיפים יהיה את הנוף הטוב ביותר, כמה שפחות (בתנאים הקיימים) נשתלים בצד הצפוני והמזרחי של המטע. כמובן שבהוצאת קבוצה של עשרה עצים (דובדבן או שזיף, לפי העניין) מתעלמים מכל העצים המפרידים. זאת אומרת, ארבעה עצים יכולים להיות בקו ישר ללא קשר לעצים אחרים (או לבית) שנמצאים ביניהם. אחרי החידה האחרונה זה יהיה די קל.
מקורות:
האיור הוא תוכנית של קוטג' כפי שהוא עומד מוקף במטע של חמישים וחמישה עצים. עשרה מהעצים הללו הם דובדבנים, עשרה הם שזיפים, והשאר תפוחים. הדובדבנים נשתלו כך שייצרו חמישה קווים ישרים, עם ארבעה עצי דובדבן בכל קו. עצי השזיף נשתלו גם הם כך שייצרו חמישה קווים ישרים עם ארבעה עצי שזיף בכל קו. החידה היא להראות אילו הם עשרת עצי הדובדבן ואילו הם עשרת עצי השזיף. על מנת שלדובדבנים ולשזיפים יהיה את הנוף הטוב ביותר, כמה שפחות (בתנאים הקיימים) נשתלים בצד הצפוני והמזרחי של המטע. כמובן שבהוצאת קבוצה של עשרה עצים (דובדבן או שזיף, לפי העניין) מתעלמים מכל העצים המפרידים. זאת אומרת, ארבעה עצים יכולים להיות בקו ישר ללא קשר לעצים אחרים (או לבית) שנמצאים ביניהם. אחרי החידה האחרונה זה יהיה די קל.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 207
-
עשרת המטבעות
הניחו עשרה מטבעות פני על גיליון נייר או קרטון גדול, כפי שמוצג בתרשים, חמישה על כל קצה. כעת הסירו ארבעה מהמטבעות, מבלי להפריע לאחרים, והחזירו אותם לנייר כך שעשרת המטבעות ייצרו חמישה קווים ישרים עם ארבעה מטבעות בכל קו. זה כשלעצמו אינו קשה, אבל עליכם לנסות לגלות בכמה דרכים שונות ניתן לפתור את החידה, בהנחה שבכל מקרה שתי השורות בהתחלה זהות לחלוטין.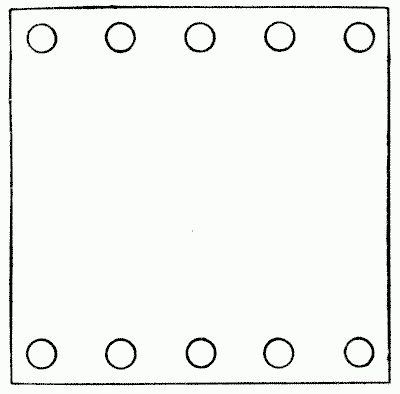 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 210
-
תריסר פשטידות בשר
ניתן לראות באיור שלנו כיצד ניתן להניח תריסר פשטידות בשר על השולחן כך שייצרו שש שורות ישרות עם ארבע פשטידות בכל שורה. החידה היא להסיר רק ארבע מהן למיקומים חדשים כך שיהיו שבע שורות ישרות עם ארבע בכל שורה. אילו ארבע הייתם מסירים, והיכן הייתם מחליפים אותן?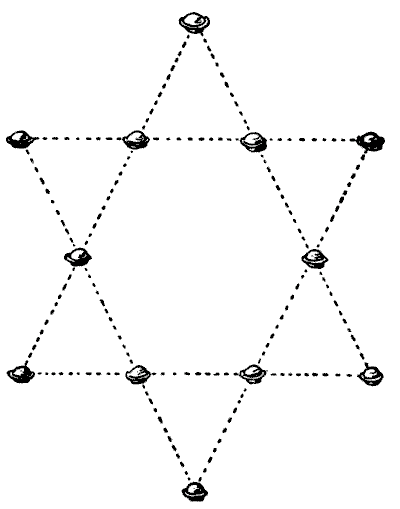 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 211
-
כשל לוח שחמט
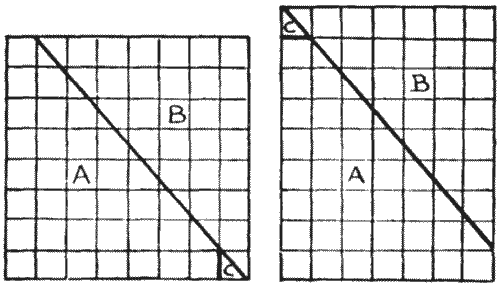
"הנה דיאגרמה של לוח שחמט," הוא אמר. "אתם רואים שיש שישים וארבעה ריבועים—שמונה על שמונה. עכשיו אני מצייר קו ישר מהפינה השמאלית העליונה, היכן שהריבוע הראשון והשני נפגשים, אל הפינה הימנית התחתונה. אני גוזר לאורך הקו הזה עם המספריים, מחליק למעלה את החלק שסימנתי B, ואז גוזר את הפינה הקטנה C על ידי חיתוך לאורך הקו הישר הראשון. החלק הקטן הזה יתאים בדיוק למקומו למעלה, ועכשיו יש לנו מלבן עם שבעה ריבועים מצד אחד ותשעה ריבועים מצד שני. לכן, יש עכשיו רק שישים ושלושה ריבועים, מכיוון ששבע כפול תשע יוצר שישים ושלוש. לאן לעזאזל נעלם הריבוע האבוד הזה? ניסיתי שוב ושוב לתפוס את הקטן המנוול, אבל הוא תמיד מתחמק ממני. בשביל החיים שלי אני לא מצליח לגלות איפה הוא מסתתר."
"זה נראה כמו הכשל הישן האחר של לוח השחמט, ואולי ההסבר זהה," אמר רג'ינלד—"שהחלקים לא מתאימים בדיוק."
"אבל הם כן מתאימים," אמר הדוד ג'ון. "נסה את זה, ותראה."
מאוחר יותר באותו ערב נראו רג'ינלד וג'ורג' בפינה כשהראשים שלהם ביחד, מנסים לתפוס את הריבוע הקטן החמקמק הזה, וזה רק הוגן לציין שלפני שהם פרשו ללילה הם הצליחו לתפוס את הטרף שלהם, אם כי חלק מחברי החברה לא הצליחו לראות אותו כשנתפס. האם הקורא יכול לפתור את התעלומה הקטנה?
מקורות:נושאים:גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 413
-
שאלה
ישנו שולחן ביליארד שצורתו משולש שהזוויות שלו שוות ל-\(90^{\circ}\), \(30^{\circ}\) ו- \(60^{\circ}\).
נתון שולחן ביליארד שצורתו משולש ישר זווית, עם "כיסים" בפינותיו. אחת מזוויותיו החדות בת \(30^{\circ}\). מהפינה הזו (בת השלושים מעלות) יוצא כדור אל אמצע הצלע הנגדית של המשולש (תיכון). הוכח, שאם הכדור הוחזר יותר משמונה פעמים, (זווית פגיעה שווה לזווית החזרה) אז בסופו של דבר הכדור ייכנס לתוך ה"כיס" שנמצא בפינה בת ה-60 מעלות של המשולש.
נושאים:גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> שיקוף