גאומטריה, גאומטריה במישור

גאומטריה במישור עוסקת בצורות וגופים על משטח שטוח ודו-ממדי. היא מכסה תכונות של נקודות, קווים, זוויות, מצולעים (כמו משולשים ומרובעים) ומעגלים. שאלות כוללות בדרך כלל הוכחות, בנייה וחישובים הקשורים לאלמנטים אלו.

חשבון שטחים משולשים מעגלים סימטריה חשבון זוויות משפט פיתגורס אי שוויון המשולש

  • איך שגלגל מסתובב לו

    כל 6 הגלגלים שבשרטוט מסתובבים כשהם נוגעים זה בזה ללא החלקה. קוטרו של הגלגל השמאלי 15.7 ס"מ והוא מבצע 12 סיבובים בדקה.

    ידוע שהגלגל הקטן מבצע סיבוב אחד בשנייה.

    מהו קוטרו של הגלגל הקטן?

    מקורות:

  • שאלה

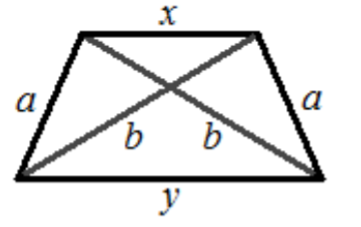
    נתון טרפז שווה שוקיים, שאורך השוק שלו a, ואורך האלכסון שלו b, כמו בציור. מצא את הערך הגדול ביותר והקטן ביותר שיכולה לקבל מכפלת הבסיסים (התשובה תלויה ב-`a` וב-`b`).

    מקורות:

  • שאלה

    נתונים שלושה מעגלים שקוטריהם 3, 4, 5. המעגלים הקטנים
    משיקים למעגל הגדול מבפנים, בנקודות נגדיות (ראה ציור). המעגלים
    הקטנים מחלקים את המעגל הגדול למספר חלקים. ניקח חלק אשר
    צורתו "משולש עקום", כלומר, הוא כלוא בין שלוש קשתות של מעגלים שונים. נסמן את
    שטחו ב-S, ואת שטח החיתוך של שני העיגולים הקטנים ב-T. חשב את `T/S`
    מקורות:

  • התבוננות לקויה

    ההתבוננות שלנו בדברים קטנים היא לעתים קרובות לקויה, והזיכרונות שלנו נוטים מאוד לחלוף. שופט מסוים העיר לאחרונה במקרה שאין לו שום זיכרון מלבישת טבעת הנישואין על אצבעה של אשתו. האם תוכלו לענות נכונה על השאלות הבאות מבלי לראות את המטבעות? באיזה צד של פני מצוין התאריך? יש אנשים כל כך לא מתבוננים שלמרות שהם מטפלים במטבע כמעט כל יום בחייהם, הם מתקשים לענות על השאלה הפשוטה הזו. אם אני מניח פני שטוח על השולחן, כמה פני אחרים אני יכול להניח סביבו, כשכל אחד מהם מונח שטוח על השולחן, כך שכולם יגעו בראשון? הגיאומטריקן כמובן ייתן את התשובה מיד, ולא יצטרך לערוך ניסוי. הוא גם יידע שמאחר שכל המעגלים דומים, אותה תשובה בהכרח תחול על כל מטבע. השאלה הבאה היא מעניינת ביותר לשאול חברה, כאשר כל אדם כותב את תשובתו על פיסת נייר, כך שאף אחד לא ייעזר בתשובות של אחרים. מהו המספר הגדול ביותר של מטבעות של שלושה פני שאפשר להניח שטוחים על פני השטח של חצי כתר, כך שאף מטבע לא יהיה מונח על אחר או יחפוף את פני השטח של חצי הכתר? זה מדהים איזו מגוון תשובות שונות מקבלים לשאלה זו. מעט מאוד אנשים יימצאו את המספר הנכון. כמובן שיש לתת את התשובה מבלי להסתכל על המטבעות. מקורות:

  • הנקודה על השולחן

    ילד, שחזר לאחרונה מבית הספר, רצה להציג לאביו את פיקחותו. הוא דחף שולחן עגול גדול לפינת החדר, כפי שמוצג באיור, כך שהוא נגע בשני הקירות, ואז הצביע על כתם דיו בקצה השולחן.

     

    "הנה חידה קטנה בשבילך, אבא," אמר הילד. "הנקודה הזו נמצאת בדיוק שמונה אינץ' מקיר אחד ותשעה אינץ' מהקיר השני. האם תוכל לומר לי מה קוטר השולחן מבלי למדוד אותו?"

    הילד נשמע אומר לחבר, "זה ממש ניצח את אבא;" אבל ידוע שהאב העיר למכר בעיר שהוא פתר את העניין בראשו תוך דקה. אני לעתים קרובות תוהה מי דיבר אמת.

    מקורות:

  • חידת הלחמנייה

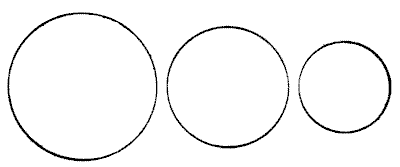    שלושת העיגולים מייצגים שלוש לחמניות, ונדרש פשוט להראות כיצד ניתן לחלק אותן באופן שווה בין ארבעה בנים. יש להתייחס ללחמניות כבעלות עובי שווה לכל אורכן ועובי שווה זו לזו. כמובן, יש לחתוך אותן למספר החלקים המועט ביותר האפשרי. כדי לפשט זאת, אציין את העובדה המפתיעה למדי שדי בחמישה חלקים בלבד, ומכך ניתן יהיה לראות שנער אחד מקבל את חלקו בשני חלקים ושלושת האחרים מקבלים את חלקם בחלק אחד. אני מודע לכך שהצהרה זו "מסגירה" את החידה, אך היא לא אמורה לפגוע בעניינם של אלה שאוהבים לגלות את "הסיבה לכך". מקורות:

  • המונד הגדול

     

    הנה סמל בעל עתיקות עצומה הראוי לתשומת לב. הוא מוטבע על נס קוריאה ועל דגל הסוחר שלה, ואומץ כסימן מסחרי על ידי חברת הרכבות Northern Pacific, אם כי מעטים מודעים לכך שמדובר במונד הגדול, כפי שמוצג בסקיצה למטה. סימן זה עבור הסיני הוא כמו הצלב עבור הנוצרי. זהו סימן האלוהות והנצח, בעוד שני החלקים שאליהם מחולק המעגל נקראים יין ויאנג—הכוחות הזכריים והנקביים של הטבע. סופר בנושא לפני יותר משלושת אלפים שנה דיווח כי אמר בהתייחסו אליו: "הבלתי מוגבל מייצר את הקיצוניות הגדולה. הקיצוניות הגדולה מייצרת את שני העקרונות. שני העקרונות מייצרים את ארבעת הרבעים, ומארבעת הרבעים אנו מפתחים את הריבוע של שמונת הדיאגרמות של פואה-הי." אני מקווה שהקוראים לא יבקשו ממני להסביר זאת, כי אין לי מושג קלוש מה זה אומר. עם זאת, אני משוכנע שבמשך עידנים לסמל היו משמעויות נסתרות וכנראה מתמטיות עבור הסטודנט האזוטרי.

    אציג את המונד בצורתו היסודית. הנה שלוש שאלות קלות בנוגע לסמל הגדול הזה:—

    (I.) למי יש שטח גדול יותר, למעגל הפנימי המכיל את היין והיאנג, או לטבעת החיצונית?

    (II.) חלקו את היין והיאנג לארבעה חלקים באותו גודל ובאותה צורה על ידי חתך אחד.

    (III.) חלקו את היין והיאנג לארבעה חלקים באותו גודל, אך בצורה שונה, על ידי חתך ישר אחד.

    מקורות:

  • שני פרסות הסוס

    מדוע יש להתייחס לפרסות סוס כאל "מזל" הוא אחד מאותם דברים שאף אדם לא יכול להבין. זוהי אמונה טפלה עתיקה מאוד, וג'ון אוברי (`1626-1700`) אומר, "לרוב הבתים בווסט אנד של לונדון יש פרסת סוס על סף הדלת." ברחוב מונמות' היו שבע עשרה בשנת `1813` ושבע עד לשנת `1855`. אפילו לורד נלסון מסמר אחת לתורן של הספינה ויקטורי. כיום אנו מוצאים שזה יותר מועיל ל"מזל טוב" לוודא שהם ממוסמרים היטב על רגלי הסוס שאנו עומדים לנסוע בו.

    אף על פי כן, עד כמה שהפרסה, כמו הצלב קרס וסמלים אחרים שיצא לי לעסוק בהם מדי פעם, שימשה לסמל בריאות, שגשוג ורצון טוב כלפי בני אדם, אנו יכולים להתייחס אליה בכבוד מסוים. האם ייתכן שיש איזשהו מסתורין מתמטי איזוטרי או אבוד החבוי בצורת פרסת סוס? בחנתי את הנושא הזה, ואני רוצה להסב את תשומת לבם של הקוראים שלי לעובדה המדהימה ביותר שזוג פרסות הסוס המוצגות באיור שלי קשורות בצורה בולטת ויפה לעיגול, שהוא הסמל של הנצח. אני מציג את העובדה הזו בצורה של בעיה פשוטה, כדי שניתן יהיה לראות עד כמה הקשר הזה הוסתר בצורה מתוחכמת במשך עידנים רבים. הקוראים שלי ישמחו, אני יודע, כשהם ימצאו את המפתח למסתורין.

     

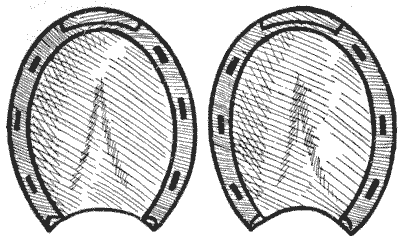
    גזרו בזהירות את שתי פרסות הסוס מסביב לקו המתאר ואז חתכו אותן לארבעה חלקים, שכולם שונים בצורתם, שיתאימו זה לזה וייצרו מעגל מושלם. כל נעל חייבת להיחתך לשני חלקים וכל החלק בטלף הסוס הכלול בתוך קו המתאר ישמש וייחשב כחלק מהשטח.

    מקורות:

  • החתולים של הקוסם

    קוסם הניח עשרה חתולים בתוך מעגל קסם כפי שמוצג באיור שלנו, והפנט אותם כך שיישארו נייחים במהלך רצונו. לאחר מכן הוא הציע לצייר שלושה מעגלים בתוך המעגל הגדול, כך שאף חתול לא יוכל להתקרב לחתול אחר מבלי לחצות מעגל קסם. נסו לצייר את שלושת המעגלים כך שלכל חתול תהיה מתחם משלו ולא יוכל להגיע לחתול אחר מבלי לחצות קו. מקורות:

  • חידת הגינה

    פרופסור רַאקְבְּרֵיין סיפר לי שעישן לאחרונה מקטרת ידידותית מתחת לעץ בגינה של מכר כפרי. הגינה הייתה מוקפת בארבעה קירות ישרים, וידידו הודיע לו שהוא מדד אותם ומצא שאורכם הוא `80, 45, 100`, ו-`63` יארד בהתאמה. "אם כך," אמר הפרופסור, "נוכל לחשב את השטח המדויק של הגינה." "זה בלתי אפשרי," השיב המארח שלו, "כי אתה יכול לקבל מספר אינסופי של צורות שונות עם ארבעת הצדדים האלה." "אבל אתה שוכח," אמר רַאקְבְּרֵיין, עם ניצוץ בעיניו, "שאמרת לי פעם ששתלת את העץ הזה במרחק שווה מכל ארבע פינות הגינה." האם תוכלו לחשב את שטח הגינה? מקורות: