几何学, 面积计算
本主题侧重于确定二维表面或区域大小的方法。问题涉及计算各种几何形状(如三角形、四边形、圆形和更复杂的组合图形)的面积,通常需要应用特定的公式。
-
面积的乘积
在图中,有一个对角线互相垂直的四边形。证明四边形内阴影区域的面积的乘积等于白色区域的面积的乘积。
来源: -
切割
从一个 `9 times 9` 的正方形中,最多可以切割出多少个 `2 times 5` 的矩形?
来源: -
灰色区域
在图中,一个矩形由 5 个大小为 `2 times 2 ` 的正方形组成,并有一条对角线穿过它。
求阴影区域的面积。
来源: -
谜题
您有一个拼图,它的每一块看起来像这样:
下面的形状由 12 块拼图组成。它的周长是多少?
来源: -
正多边形和圆
A.
在右边的图中,有一个正方形,里面有4个圆。这些圆的半径相等,每个圆与另外两个圆相切,并且与正方形的两条边相切。求正方形中蓝色部分面积与白色部分面积的比率。
B.
在左边的图中,有一个六边形,里面有6个半径相同的圆。每个圆与另外两个圆相切,并且与六边形的一条边在中间位置相切。求六边形中蓝色部分面积与白色部分面积的比率。
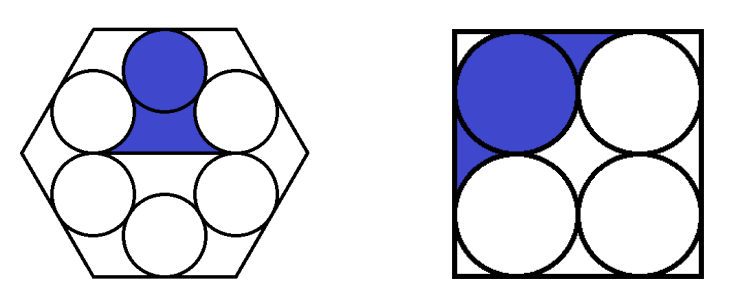
(答案格式:"x, y" 例如 "1/8, 7/100")
来源: -
直角三角形和正方形
给定大量全等的直角三角形。
每个三角形的边长分别为 3、4 和 5。
最多可以在 20×20 的正方形内放置多少个这样的三角形,使它们互不重叠?
来源: -
又一片灰色区域
图中有一个 `3 times 5` 的矩形,一条直线沿对角线将其分割。求阴影部分的面积。
来源: -
秘密区域
丹尼尔画了四个边相互平行的矩形。这些矩形形成了四个相交区域(见图)。
已知其中三个区域的面积。求第四个相交区域的面积。
来源: -
正六边形和三角形
有一个正六边形和一个等边三角形,它们的周长相等。已知三角形的面积等于 60。求六边形的面积。
来源: -
正方形之和
已知一个矩形的面积为 13,周长为 20。在该矩形的两条相邻边上构造两个正方形,如图所示。求这两个正方形的面积之和。
来源:







