几何学, 面积计算
本主题侧重于确定二维表面或区域大小的方法。问题涉及计算各种几何形状(如三角形、四边形、圆形和更复杂的组合图形)的面积,通常需要应用特定的公式。
-
问题
在图中,有一个半圆,其中包含三个圆:一个大圆,它与半圆的直径在其中心相切,以及两侧对称的两个小圆。哪个面积更大:阴影区域还是空白区域?
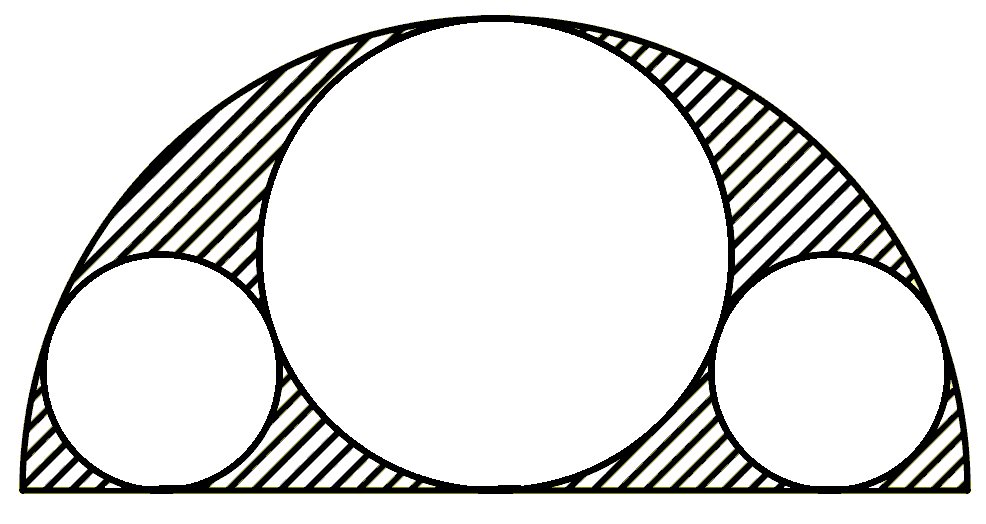
-
阴阳四分之一
图中形状的构造方式如下:将半圆的直径分成两个相等的部分,并以它们为直径构建另外两个半圆:一个在内部,另一个在外部。
将该形状分成两个全等的部分。
-
问题
给定一个 `10×10` 厘米的纸。你能否从这张纸上剪出若干个圆,使得它们的直径之和大于 `5` 米?
-
问题
已知给定形状的所有角都是直角。将形状切割成两个面积相等的多边形。 只允许使用没有刻度的直尺。
-
问题
两个全等的三角形形成一个如图像所示的六芒星。证明阴影区域的面积等于条纹区域的面积。
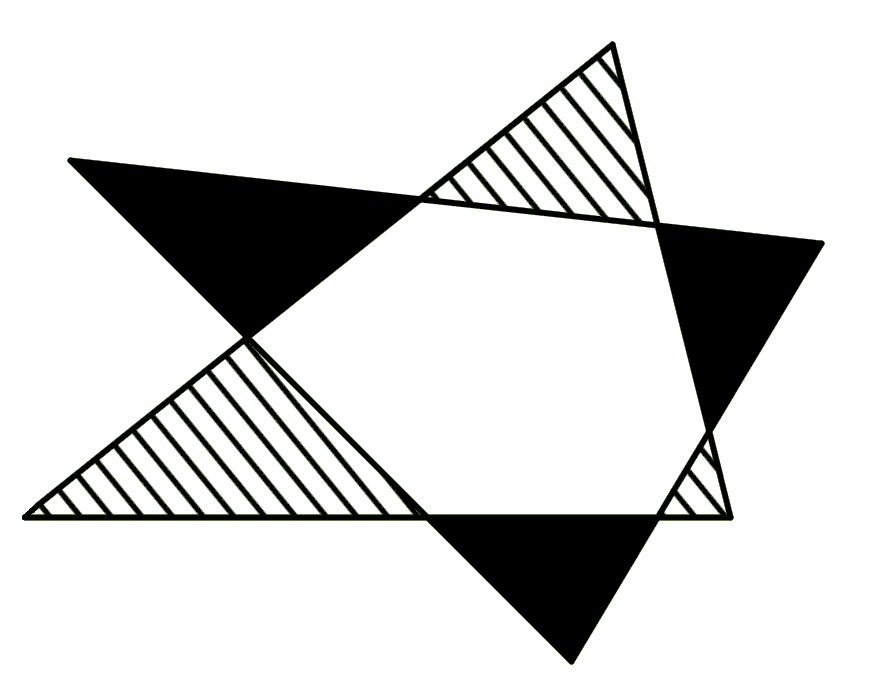
-
问题
你能否将一个 `5xx5` 的矩形放入一个 `4xx6` 的矩形中?
-
形状的面积
给定一个方格纸,其中每个方格的面积是一个面积单位。求出该形状的面积(以面积单位计)。
来源: -
问题
在一个边长为1的正方形内,标记了 `n>=101` 个点,其中任意三点都不共线。如果一个三角形的顶点都是被标记的点,则称其为标记三角形。证明存在一个标记三角形,其面积小于 `1/100`
来源: -
六边形
图中是一个正六边形。白色区域的面积是阴影区域面积的多少倍?
(正六边形是指所有边都相等且所有角都相等的六边形)
来源: -
面积的乘积
在一个矩形内有一个点。通过该点作两条分别平行于矩形两边的线段,将矩形分割成4个更小的矩形。
证明矩形内阴影区域的面积乘积等于白色区域的面积乘积。来源:




