代数学, 方程
方程是陈述两个数学表达式相等的语句。解方程涉及找到使语句为真的变量值。问题涵盖各种类型:线性、二次、多项式、有理、根式和方程组。
丢番图方程-
问题
有三个装有坚果的袋子。第一个袋子里的坚果比其他两个袋子加起来少`6`公斤。第二个袋子里的坚果比其他两个袋子加起来少`10`公斤。
第三个袋子里有多少公斤坚果?
来源: -
不安分的苍蝇
城市 A 和 B 相距 300 公里。两名自行车手同时从 A 和 B 出发,彼此相向而行。 他们的速度恒定,分别为 `30` 公里/小时 和 `20` 公里/小时。 在同一时刻,一只苍蝇从 A 市出发,以 `100` 公里/小时的速度飞行。 苍蝇超过第一位自行车手,然后飞到与从 B 市出发的自行车手相遇。 当苍蝇遇到自行车手时,它立即转身飞回,直到再次遇到第一位自行车手,然后它再次转身,依此类推,直到自行车手们相遇。 苍蝇飞了多少公里?
-
问题
尼娜和梅尔同时从他们的家出发,一起去拜访奶奶。从他们家到奶奶家的路线长 3 公里,沿途放置着长椅。
尼娜会在路上的每个长椅上坐下,吃一块饼干。她吃每块饼干的时间都是相同的整数分钟。梅尔也会停下来坐在每条长椅上吃一块饼干。
梅尔吃饼干的时间是尼娜的两倍。此外,已知尼娜的速度是每小时 3 公里,梅尔的速度是每小时 4 公里。
结果表明,梅尔和尼娜同时到达了奶奶家。
路上有多少条长椅?找出所有可能性并解释你的答案
来源: -
问题
给定一个自然数 `A`。当它增加 `1` 时,它的平方增加 `1001`。求 `A`。
-
问题
不同的实数 `x` 和 `y` 满足以下方程:
`x^2 – 2000x = y^2 – 2000y`
求 `x` 和 `y` 的和。
-
问题
解下列方程:
`(x + 2010)(x + 2011)(x + 2012) = (x + 2011)(x + 2012)(x + 2013) `
来源: -
问题
给定一个圆锥(其对称轴位于中心,垂直于其底面),其高度为 6,底面是一个半径为 `sqrt2` 的圆。圆锥内接一个立方体——它位于圆锥的底面上,并且其所有上顶点都接触圆锥。求立方体的边长。解释你的答案。
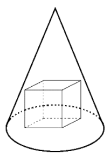 来源:
来源: -
硬币和蛋糕
玛丽姆有2谢克尔和5谢克尔的硬币。
如果她只用2谢克尔的硬币支付,她将缺少60谢克尔来购买4个蛋糕。
如果她只用5谢克尔的硬币支付,她将缺少60谢克尔来购买5个蛋糕。
总共她缺少60谢克尔来购买6个蛋糕。一个蛋糕多少钱?
来源: -
问题
已知 `a+b-c=6`, `ac+bc-ab=2`. 求解 `a^2+b^2+c^2`.
-
问题
已知实数 `a`、`b` 和 `c` 均不等于 `0`,且满足:`a+b/c=b+c/a=c+a/b=1`。证明:`ab+bc+ca=0`。