גאומטריה

גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.

גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים

• חידת חיתוך קלה

   

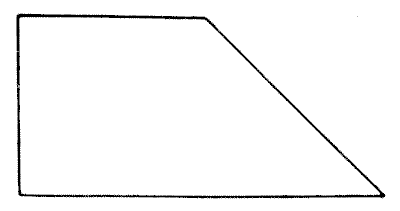
  ראשית, גזרו פיסת נייר או קרטון בצורה המוצגת באיור. ניתן לראות מיד שהפרופורציות הן פשוט אלו של ריבוע המחובר למחצית ריבוע דומה אחר, המחולק באלכסון. החידה היא לחתוך אותו לארבעה חלקים, כולם באותו גודל וצורה בדיוק.

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 146

• חידת ריבוע קלה

   

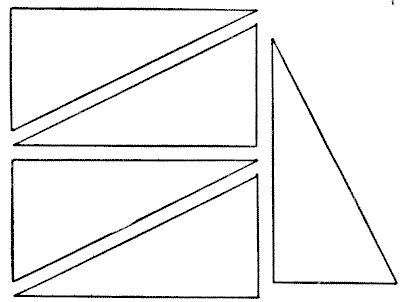
  אם תיקח פיסת קרטון מלבנית, שאורכה כפול מרוחבה, ותחתוך אותה לשניים באלכסון, תקבל שניים מהחלקים המוצגים באיור. החידה היא ליצור ריבוע מחמישה חלקים כאלה בגודל שווה. ניתן לחתוך אחד מהחלקים לשניים, אך יש להשתמש בשאר החלקים בשלמותם.

  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 147

• חידת הלחמנייה

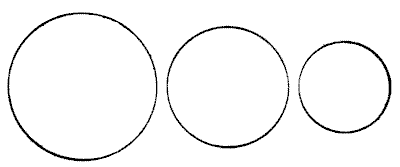  שלושת העיגולים מייצגים שלוש לחמניות, ונדרש פשוט להראות כיצד ניתן לחלק אותן באופן שווה בין ארבעה בנים. יש להתייחס ללחמניות כבעלות עובי שווה לכל אורכן ועובי שווה זו לזו. כמובן, יש לחתוך אותן למספר החלקים המועט ביותר האפשרי. כדי לפשט זאת, אציין את העובדה המפתיעה למדי שדי בחמישה חלקים בלבד, ומכך ניתן יהיה לראות שנער אחד מקבל את חלקו בשני חלקים ושלושת האחרים מקבלים את חלקם בחלק אחד. אני מודע לכך שהצהרה זו "מסגירה" את החידה, אך היא לא אמורה לפגוע בעניינם של אלה שאוהבים לגלות את "הסיבה לכך".
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 148

• ריבועי השוקולד

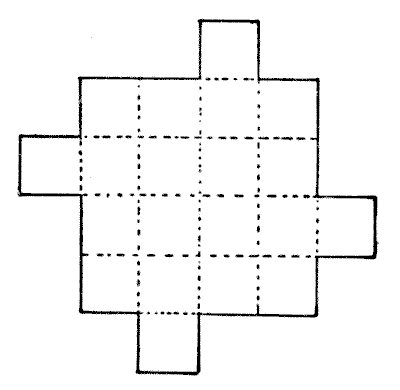  הנה לוח שוקולד, עם שקעים בקווקווים כך שאפשר להפריד בקלות את עשרים הריבועים. הכינו העתק של הלוח מנייר או קרטון, ואז נסו לחתוך אותו לתשעה חלקים כך שייצרו ארבעה ריבועים מושלמים בגודל זהה לחלוטין.
  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 149

• חיתוך זוית

   

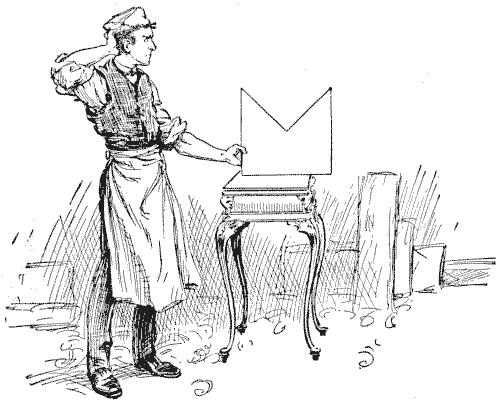
  הצורה שמבלבלת את הנגר באיור מייצגת זווית. ניתן לראות שהמידות שלה הן של ריבוע שהוסר ממנו רבע. החידה היא לחתוך אותה לחמישה חלקים שיתאימו זה לזה וייצרו ריבוע מושלם. אני מציג ניסיון, שפורסם באמריקה, לבצע את המשימה בארבעה חלקים, המבוסס על מה שידוע כ"עיקרון הצעד", אבל זו טעות.  

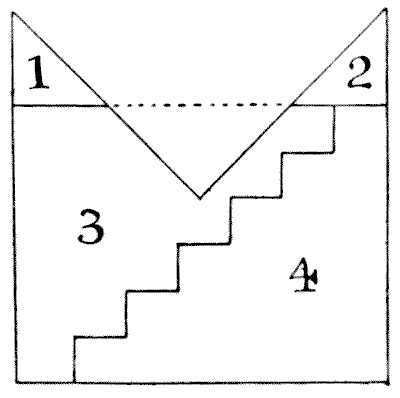
  נאמר לנו תחילה לחתוך את החלקים `1` ו-`2` ולארוז אותם בחלל המשולש המסומן על ידי הקו המקווקו, וכך ליצור מלבן.

  עד כאן טוב ויפה. עכשיו, אנו מונחים ליישם את עקרון הצעד הישן, כפי שמוצג, ועל ידי הזזת החלק `4` צעד אחד למטה, ליצור את הריבוע הנדרש. אבל, לצערי, זה לא מייצר ריבוע: רק מלבן. נקרא לשלושת הצדדים הארוכים של הזווית `84` אינץ' כל אחד. אז, לפני חיתוך הצעדים, המלבן שלנו בשלושה חלקים יהיה `84`×`63`. הצעדים צריכים להיות `10`½ אינץ' בגובה ו-`12` אינץ' ברוחב. לכן, על ידי הזזת צעד אחד למטה אנו מקטינים ב-`12` אינץ' את הצד `84` אינץ' ומגדילים ב-`10`½ אינץ' את הצד `63` אינץ'. לכן המלבן הסופי שלנו חייב להיות `72` אינץ' × `73`½ אינץ', מה שבהחלט אינו ריבוע! העובדה היא שניתן ליישם את עקרון הצעד רק על מלבנים עם צלעות באורכים יחסיים מסוימים. לדוגמה, אם הצד הקצר יותר במקרה זה היה `61` `5/7` (במקום `63`), אז שיטת הצעד תתאים. כי אז הצעדים יהיו `10` `2/7` אינץ' בגובה ו-`12` אינץ' ברוחב. שימו לב ש-`61` `5/7` × `84`= הריבוע של `72`. נכון לעכשיו לא נמצא פתרון בארבעה חלקים, ואני לא מאמין שאפשר למצוא כזה.

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 150

• הבעיה של הנגר

  לעיתים קרובות הזדמן לי להעיר על התועלת המעשית של חידות, הנובעות מיישום לענייני היומיום של הטריקים הקטנים וה-"קמטים" שאנו לומדים תוך כדי פתרון בעיות שעשוע.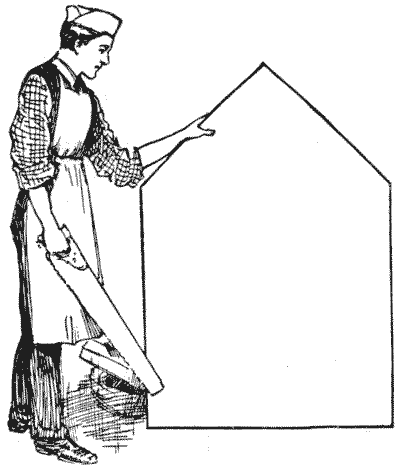 הנגר, באיור, רוצה לחתוך את חתיכת העץ למספר החלקים המינימלי האפשרי כדי ליצור משטח שולחן מרובע, מבלי לבזבז חומר. איך עליו לגשת לעבודה? כמה חלקים תצטרכו?
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 151

• בעיה נוספת של נגר

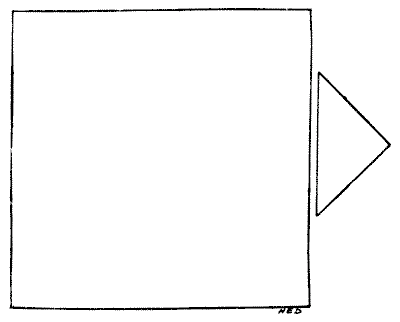  לנגר היו שני חתיכות עץ בצורות ובפרופורציות יחסיות המוצגות בדיאגרמה. הוא רצה לחתוך אותן למספר קטן ככל האפשר של חלקים כך שניתן יהיה לחבר אותם יחד, ללא בזבוז, וליצור משטח שולחן מרובע לחלוטין. איך הוא היה צריך לעשות את זה? אין צורך לתת מידות, כי אם החלק הקטן יותר (שהוא חצי ריבוע) יהיה קצת גדול מדי או קטן מדי, זה לא ישפיע על שיטת הפתרון.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 152

• פאזל גזירה

  הנה חידה קטנה בגזירה. אני לוקח רצועת נייר, בגודל חמישה אינץ' על אינץ' אחד, ובאמצעות חיתוך לחמישה חלקים, החלקים מתאימים יחד ויוצרים ריבוע, כפי שמוצג באיור. עכשיו, זהו פאזל די מעניין לגלות איך אנחנו יכולים לעשות זאת רק בארבעה חלקים.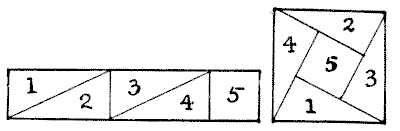
  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 153

• שטיח האח של גברת הובסון

  

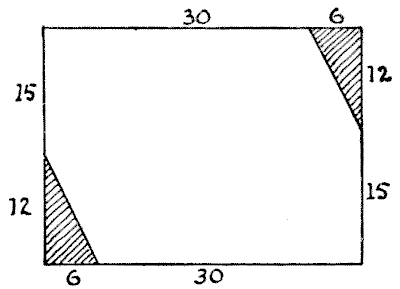
  לבנה של גברת הובסון הייתה תאונה כששיחק באש, ושרף שתיים מפינותיו של שטיח אח יפה. הפינות הפגומות נחתכו, וכעת יש לו את המראה והפרופורציות המוצגים בדיאגרמה שלי. איך גברת הובסון צריכה לחתוך את השטיח למספר המינימלי האפשרי של חלקים שיתאימו זה לזה וייצרו שטיח מרובע לחלוטין? ניתן לראות שהשטיח הוא בפרופורציות של `36` × `27` (לא משנה אם נאמר אינצ'ים או יארדים), וכל חתיכה שנחתכה הייתה במידות של `12` ו-`6` מבחוץ כמו בציור.

  נושאים:

  גאומטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 154

• המחומש והריבוע

  מעניין אותי כמה מקוראיי, מבין אלה שלא הקדישו תשומת לב רבה ליסודות הגיאומטריה, יוכלו לצייר מחומש משוכלל, או צורה בעלת חמש צלעות, אם יידרשו לעשות זאת באופן פתאומי. משושה משוכלל, או צורה בעלת שש צלעות, הוא די קל, כי כולם יודעים שכל מה שצריך לעשות הוא לתאר מעגל ואז, לקחת את הרדיוס כאורך אחת הצלעות, ולסמן את שש הנקודות סביב ההיקף. אבל מחומש הוא עניין אחר לגמרי. אז, מכיוון שהחידה שלי קשורה לחיתוך של מחומש משוכלל, אולי כדאי שאקודם כל אראה לקוראים הפחות מנוסים שלי איך יש לצייר צורה זו בצורה נכונה. תארו מעגל וציירו את שני הקווים H B ו-D G, בתרשים, דרך המרכז בזוויות ישרות. כעת מצאו את הנקודה A, באמצע בין C ו-B. לאחר מכן הניחו את חוד המצפן שלכם ב-A ועם המרחק A D תארו את הקשת החותכת את H B ב-E. לאחר מכן הניחו את חוד המצפן שלכם ב-D ועם המרחק D E תארו את הקשת החותכת את ההיקף ב-F. כעת, D F היא אחת הצלעות של המחומש שלכם, ועליכם פשוט לסמן את הצלעות האחרות סביב המעגל. די פשוט כשאתם יודעים איך, אבל אחרת קצת קשה.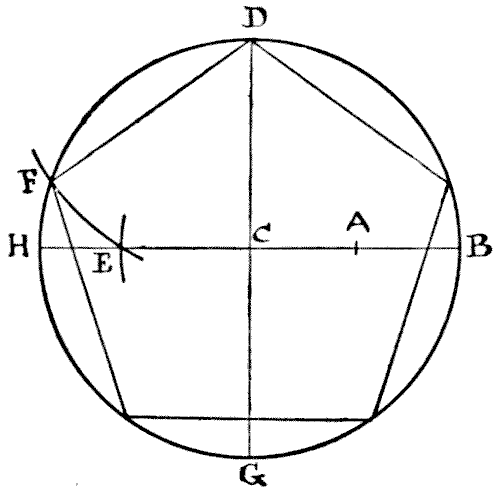 לאחר שיצרתם את המחומש שלכם, החידה היא לחתוך אותו למספר המועט ביותר של חלקים שיתאימו זה לזה וייצרו ריבוע מושלם.
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 155