גאומטריה

גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.

גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים

• הגדלת מלבן

  נתון מלבן במישור. האם יכול להיות שאחרי שכל צלע של המלבן הוגדלה ב 1 ס"מ השטח גדל ב 1 מ"ר? הביאו דוגמא או הוכיחו שזה בלתי אפשרי.

  (אם המלבן הוא 1x5 אז הוא הופך ל 2x6 ואף צלע לא יכולה להיות 0)

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> חשבון שטחים אלגברה -> משוואות אלגברה -> בעיות מילוליות
  מקורות:
  • תחרות גרוסמן, 2017, צעירים שאלה 1

• שאלה

  בתוך ריבוע ABCD שאורך צלעו 1 סומנה נקודה E, ומחוץ לריבוע נקודה F, כך שהמשולשים ABE ו-DAF משוכללים. חשבו את השטח של המחומש CBEFD.
  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> סימטריה גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> סיבוב
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 6

• שאלה

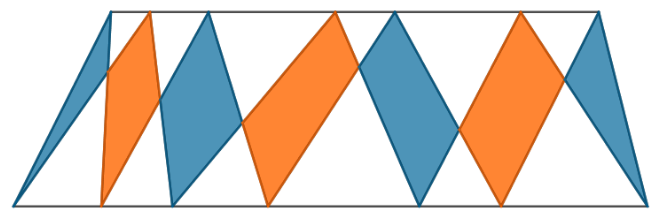
  בציור מצויר טרפז, שעל כל בסיס שלו נבחרו 5 נקודות. חלק מהנקודות חוברו על ידי קטעים ישרים. הראו כי סכום השטחים הכחולים שווה לסכום השטחים הכתומים.
  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים
  מקורות:
  • אולימפיאדת בנו ארבל, 2019, כיתה ח שאלה 5

• שאלה

  חלק את הצורה שבציור לשלושה חלקים שווים בשטחם ובצורתם.
  

  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 4

• שאלה

  נתון מצולע משוכלל. על כל צלע בונים משולש ישר זווית ושווה-שוקיים, כך שהצלע היא היתר של המשולש, וקודקוד הראש בפנים המצולע. מחברים את קודקודי הראש של כל המשולשים ומקבלים מצולע (משוכלל, בעל אותו מספר צלעות). כמה צלעות יש למצולע המקורי, אם שטחו של המצולע שהתקבל הוא חצי משטח המצולע המקורי?

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 7

• שאלה

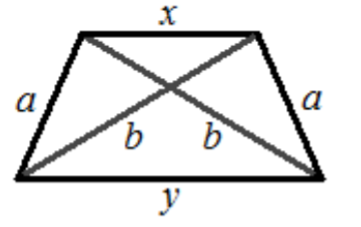
  נתון טרפז שווה שוקיים, שאורך השוק שלו a, ואורך האלכסון שלו b, כמו בציור. מצא את הערך הגדול ביותר והקטן ביותר שיכולה לקבל מכפלת הבסיסים (התשובה תלויה ב-`a` וב-`b`).
  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 9

• שאלה

  נתונים שלושה מעגלים שקוטריהם 3, 4, 5. המעגלים הקטנים
  משיקים למעגל הגדול מבפנים, בנקודות נגדיות (ראה ציור). המעגלים
  הקטנים מחלקים את המעגל הגדול למספר חלקים. ניקח חלק אשר
  צורתו "משולש עקום", כלומר, הוא כלוא בין שלוש קשתות של מעגלים שונים. נסמן את
  שטחו ב-S, ואת שטח החיתוך של שני העיגולים הקטנים ב-T. חשב את `T/S`
  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"ב, שלב א שאלה 5

• שאלה

  נתון משולש ABC ומעגל עם רדיוס 10 שחותך כל אחד מהצלעות של המשולש בשתי נקודות: נקודות
  P ו-Q על הצלע BC, נקודות K ו-L על הצלע CA, ונקודות M ו-N על הצלע AB, כך שמתקיים `AM = MN = KL = PQ = 2PB = BC/6`. מצאו את שטח המשולש ABC.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> מעגלים
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשפ"ה, שלב ב שאלה 6

• קצירת התירס

  לחקלאי הייתה שדה תירס בצורת ריבוע. התירס היה בשל לקציר, ומכיוון שהיו לו מעט עובדים, הוסכם שהוא ובנו יחלקו את העבודה ביניהם. החקלאי קצר תחילה רצועה ברוחב מוט אחד מסביב לכל הריבוע, ובכך הותיר ריבוע קטן יותר של תירס עומד באמצע השדה. "כעת," אמר לבנו, "קצרתי את החצי שלי מהשדה, ואתה יכול לעשות את החלק שלך." הבן לא היה מרוצה לחלוטין מחלוקת העבודה המוצעת, ומכיוון שמורה הכפר עבר במקרה, הוא פנה לאדם זה כדי שיכריע בעניין. הוא גילה שהחקלאי צדק לחלוטין, בתנאי שלא היה ויכוח על גודל השדה, ובנקודה זו הם הסכימו. האם תוכלו לומר מהו שטח השדה, כפי שהמורה הממולח הצליח לעשות?
  נושאים:

  גאומטריה -> חשבון שטחים אלגברה -> משוואות אלגברה -> בעיות מילוליות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 111

• בעיית גדר

  התועלת המעשית של חידות היא נקודה שאנו עלולים להתעלם ממנה. עם זאת, למעשה, מדי פעם קיבלתי מספר רב למדי של מכתבים מאנשים שמצאו שהשתלטות על עיקרון קטן שעליו נבנתה חידה, הוכיחה את עצמה כבעלת ערך רב עבורם בצורה בלתי צפויה ביותר. אכן, ניתן לקבל כעיקרון טוב שלחידה יש ערך מועט אמיתי אלא אם כן, בנוסף להיותה משעשעת ומבלבלת, היא מסתירה איזו תכונה מועילה ואולי מועילה. עם זאת, זה מאוד מוזר איך פיסות ידע נרכש קטנות אלה משתלבות בדרישות המזדמנות של חיי היומיום, ומוזר באותה מידה לאילו שימושים מוזרים ומסתוריים חלק מהקוראים שלנו נראים כמיישמים אותם. מה, למשל, יכול להיות המטרה של מר Wm. אוקסלי, שכותב לי מכל הדרך מאיווה, בבקשה לברר את ממדי השדה שהוא מציע לגדר, המכיל בדיוק את אותו מספר דונמים כמו שיש מעקות בגדר? האיש רוצה לגדר שדה מרובע לחלוטין שאמור להכיל בדיוק את אותו מספר דונמים כמו שיש מעקות בגדר הנדרשת. כל מכשול, או חלק מהגדר, הוא בגובה שבעה מעקות, ושני אורכים ימתחו מוט אחד (`16`½ רגל): כלומר, ישנם ארבעה עשר מעקות למוט, מידה קווית. עכשיו, מה צריך להיות גודל השדה?
  נושאים:

  גאומטריה -> חשבון שטחים אלגברה -> בעיות מילוליות יחידות מידה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 117