גאומטריה

גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.

גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים

• חידת הגינה

  פרופסור רַאקְבְּרֵיין סיפר לי שעישן לאחרונה מקטרת ידידותית מתחת לעץ בגינה של מכר כפרי. הגינה הייתה מוקפת בארבעה קירות ישרים, וידידו הודיע לו שהוא מדד אותם ומצא שאורכם הוא `80, 45, 100`, ו-`63` יארד בהתאמה. "אם כך," אמר הפרופסור, "נוכל לחשב את השטח המדויק של הגינה." "זה בלתי אפשרי," השיב המארח שלו, "כי אתה יכול לקבל מספר אינסופי של צורות שונות עם ארבעת הצדדים האלה." "אבל אתה שוכח," אמר רַאקְבְּרֵיין, עם ניצוץ בעיניו, "שאמרת לי פעם ששתלת את העץ הזה במרחק שווה מכל ארבע פינות הגינה." האם תוכלו לחשב את שטח הגינה?
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה -> משוואות אלגברה -> בעיות מילוליות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 182

• הדגל של סנט ג'ורג'

  במהלך חגיגה של הפסטיבל הלאומי של יום סנט ג'ורג', התבוננתי בדגל המוכר של הפטרון של ארצנו. כולנו מכירים את הצלב האדום על רקע לבן, כפי שמוצג באיור שלנו. זהו הדגל של סנט ג'ורג'. הדגל של סנט אנדרו (סקוטלנד) הוא "הצלב של סנט אנדרו" לבן על רקע כחול. הדגל של סנט פטריק (אירלנד) הוא צלב דומה באדום על רקע לבן. שלושתם מאוחדים לאחד כדי ליצור את היוניון ג'ק שלנו.

  עכשיו, בהתבוננות בדגל של סנט ג'ורג', עלתה בדעתי השאלה הבאה שיכולה להוות חידה קטנה אך נחמדה. נניח שהדגל מודד ארבע רגליים על שלוש רגליים, כמה רחבה צריכה להיות זרוע הצלב אם נדרש להשתמש בדיוק באותה כמות של בד אדום ולבן?

  

  נושאים:

  גאומטריה -> חשבון שטחים אלגברה -> בעיות מילוליות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 185

• אחוזות יורקשייר

   

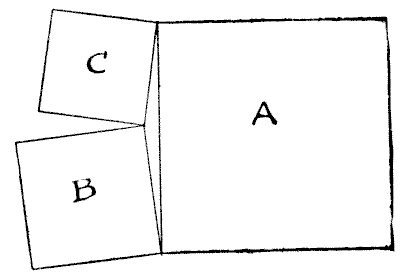
  ביקרתי באחת הערים הגדולות של יורקשייר. בדרכי לתחנת הרכבת ביום עזיבתי, אדם דחף לי עלון, לקחתי אותו לקרון הרכבת וקראתי אותו בשעות הפנאי שלי. הוא הודיע לי ששלוש אחוזות שכנות ביורקשייר מוצעות למכירה. כל אחוזה הייתה בצורת ריבוע, והן הצטרפו זו לזו בפינותיהן, בדיוק כפי שמוצג בתרשים. אחוזה A מכילה בדיוק `370` אקרים, B מכילה `116` אקרים, ו-C `74` אקרים.

  כעת, פיסת הקרקע המשולשת הקטנה התחומה על ידי שלוש האחוזות הריבועיות לא הוצעה למכירה, ומסיבה לא מיוחדת, התעוררתי לסקרנות לגבי שטח החלקה הזו. כמה אקרים היא הכילה?

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 189

• האחוזה של החוואי וורצל

   

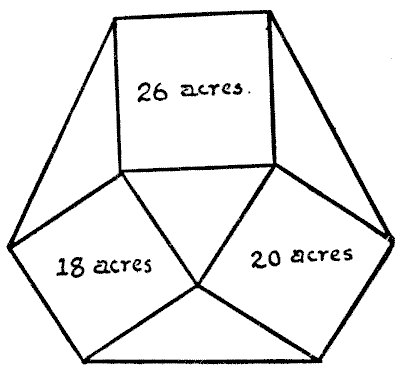
  אציג כעת בעיית שטח נוספת. ההדגמה של התשובה שאציג, אני חושב, תימצא גם מעניינת וגם קלה להבנה.

  החוואי וורצל היה הבעלים של שלושה שדות מרובעים כפי שמוצג בתוכנית המצורפת, המכילים בהתאמה `18, 20`, ו-`26` אקרים. כדי להקיף את רכושו בגדר טבעת, הוא קנה את ארבעת השדות המשולשים המפרידים. החידה היא לגלות מה היה אז השטח הכולל של האחוזה שלו.

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 190

• מִכְלָא הַצֹּאן

  זהו עובדה מוזרה שהתשובות שניתנות תמיד לכמה מהחידות הידועות ביותר המופיעות בכל ספר קטן של שעשועי בית שפורסם בחמישים או מאה השנים האחרונות הן או בלתי מספקות לחלוטין או שגויות בבירור. עם זאת, נראה שאף אחד לא מבחין בפגמים שלהן. הנה דוגמה: - לחקלאי היה מכלאה העשויה מחמישים גדרות, המסוגלת להכיל רק מאה כבשים. נניח שהוא רצה להגדיל אותו מספיק כדי להכיל כפול ממספר זה, כמה גדרות נוספות הוא צריך?
  נושאים:

  גאומטריה -> חשבון שטחים לוגיקה -> הגיון
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 193

• חומות הגן

   

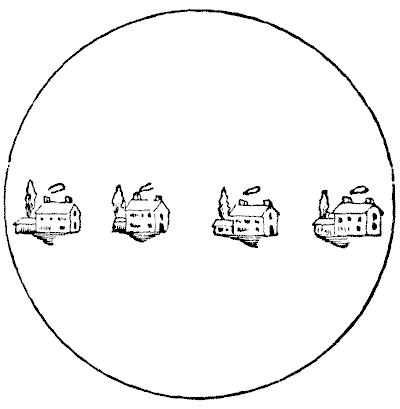
  יזם נדל"ן ספקולטיבי מחזיק בשדה עגול, עליו הקים ארבעה קוטג'ים, כפי שמוצג באיור. השדה מוקף בחומה מלבנים, והבעלים התחייב להקים עוד שלושה קירות לבנים, כך שהשכנים לא יוכלו להציץ אחד לשני, אך ארבעת הדיירים מתעקשים שלא תהיה אפליה, ושלכל אחד יהיה בדיוק אותו אורך שטח קיר לעצי הפרי שלו. החידה היא להראות כיצד ניתן לבנות את שלושת הקירות כך שלכל דייר יהיה אותו שטח אדמה, ובדיוק אותו אורך של קיר.

  כמובן, כל גן חייב להיות סגור לחלוטין על ידי קירותיו, וחייב להיות אפשרי להוכיח שלכל גן יש בדיוק אותו אורך של קיר. אם החידה נפתרת כראוי, אין צורך במספרים.

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 194

• העז הקשורה

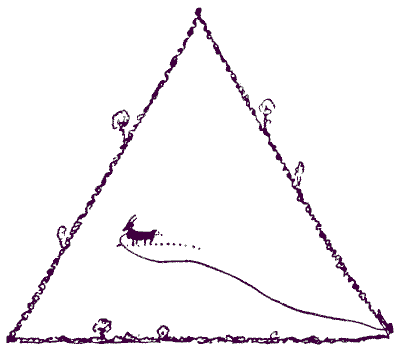  הנה בעיה קטנה שכל אחד צריך לדעת איך לפתור. העז ממוקמת באחו בשטח של חצי אקר, אשר צורתו משולש שווה צלעות. היא קשורה לעמוד בפינה אחת של השדה. מה צריך להיות אורך החבל (באינץ' הקרוב ביותר) כדי שהעז תוכל לאכול רק חצי מהדשא בשדה? ההנחה היא שהעז יכולה לאכול עד סוף החבל.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> חשבון זוויות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 196

• חידת גפרורים חדשה

  באיור מוצגים שמונה-עשר גפרורים המסודרים כך שהם תוחמים שני שטחים, כאשר אחד גדול פי שניים מהשני. האם תוכלו לסדר אותם מחדש (`1`) כך שיתחמו שני שטחים מרובעים, כאשר אחד גדול בדיוק פי שלושה מהשני, ו- (`2`) כך שיתחמו שני שטחים מחומשים, כאשר אחד גדול בדיוק פי שלושה מהשני? יש להשתמש בכל שמונה-עשר הגפרורים בצורה הוגנת בכל מקרה; שני השטחים חייבים להיות מופרדים לחלוטין, ולא צריכים להיות קצוות רופפים או גפרורים כפולים.
  נושאים:

  גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה חידות ורבוסים -> חידות גפרורים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 204

• ספירת מלבנים

  האם תוכל לומר נכון כמה ריבועים ומלבנים אחרים מכילה לוח השחמט? במילים אחרות, בכמה דרכים שונות אפשר לציין ריבוע או מלבן אחר התחום על ידי קווים המפרידים בין ריבועי הלוח?
  נושאים:

  קומבינטוריקה גאומטריה -> חשבון שטחים תורת המספרים -> מספרים משולשיים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 347

• שאלה

  ישנו שולחן ביליארד שצורתו משולש שהזוויות שלו שוות ל-\(90^{\circ}\), \(30^{\circ}\) ו- \(60^{\circ}\). 

   

  נתון שולחן ביליארד שצורתו משולש ישר זווית, עם "כיסים" בפינותיו. אחת מזוויותיו החדות בת \(30^{\circ}\). מהפינה הזו (בת השלושים מעלות) יוצא כדור אל אמצע הצלע הנגדית של המשולש (תיכון). הוכח, שאם הכדור הוחזר יותר משמונה פעמים, (זווית פגיעה שווה לזווית החזרה) אז בסופו של דבר הכדור ייכנס לתוך ה"כיס" שנמצא בפינה בת ה-60 מעלות של המשולש.

  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> שיקוף