גאומטריה

גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.

גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים

• משולשים על קוים

  שישה משולשים שווי שוקיים חופפים הוצמדו זה לזה כמתואר בציור.
  הראו כי הנקודות C, F ו- M נמצאות על ישר אחד.

  

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במישור -> משולשים -> חפיפת משולשים גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות) -> הזזה במקביל
  מקורות:
  • אולימפיאדת גיליס, תשע"ט שאלה 3

• ריצוף משושה

  נתונים שני סוגים של מרצפות. צורתה של כל מרצפת מהסוג הראשון היא משושה משוכלל בעל צלע באורך 1. צורתה של כל מרצפת מהסוג השני היא משושה משוכלל בעל צלע באורך 2. נתון מלאי בלתי מוגבל של מרצפות מכל אחד מהסוגים. האם ניתן לרצף את כל המישור באמצעות מרצפות אלו, תוך שימוש בכל אחד משני סוגי המרצפות?

  נושאים:

  לוגיקה -> הגיון הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במישור -> חשבון זוויות
  מקורות:
  • תחרות גרוסמן, 2006 שאלה 4

• שאלה

  בשעה 12:00 מחוגי השעון מתלכדים. כמה זמן יעבור עד שהמחוגים יהיו מאונכים זה לזה בפעם הראשונה? (המחוגים נעים ברציפות, במהירויות קבועות)

  נושאים:

  אלגברה -> משוואות אלגברה -> בעיות מילוליות -> בעיות תנועה גאומטריה -> גאומטריה במישור -> חשבון זוויות
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 2

• שעון בתחנת רכבת

  שעון תלוי על קיר בתחנת רכבת, שאורכו `71` רגל `9` אינץ' וגובהו `10` רגל `4` אינץ'. אלו הם מידות הקיר, לא של השעון! בזמן שחיכינו לרכבת, שמנו לב שהמחוגים של השעון מצביעים בכיוונים מנוגדים, והיו מקבילים לאחד האלכסונים של הקיר. מה הייתה השעה המדויקת?
  נושאים:

  אלגברה -> בעיות מילוליות אריתמטיקה -> שברים גאומטריה -> גאומטריה במישור -> חשבון זוויות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 65

• מרוץ היאכטות

  ובכן, יא יבשושים, הניפו את המפרשים הקדמיים הקטנים שלכם, שלפו את הספינקרים, שחררו את יריעות הבלון והכינו את מפרשי הראש שלכם!

  המרוץ שלנו מורכב מלהתחיל מהנקודה שבה היאכטה נמצאת באיור ולגעת בכל אחד משישים וארבעת המצופים בארבעה-עשר מסלולים ישרים, ולחזור בזיגזג הסופי למצוף ממנו התחלנו. המסלול השביעי חייב להסתיים במצוף שעליו מתנוסס דגל.

  חידה זו תדרוש מיומנות ימית רבה בשל הזוויות החדות שבהן יהיה צורך לעיתים לעשות זיגזג. חוד של עיפרון ועין ימית טובה הם כל הציוד שאנו זקוקים לו.  

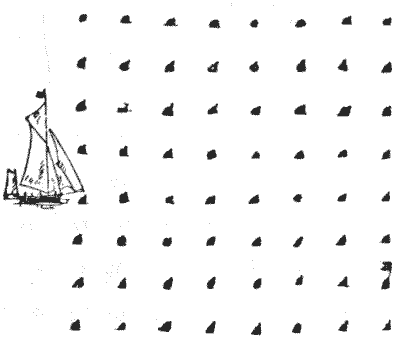
  זה קשה, בגלל התנאי לגבי מצוף הדגל, ובגלל שזהו מסלול חוזר. אבל שוב מותרים לנו הקווים האלכסוניים האלה.

  נושאים:

  גאומטריה -> גאומטריה במישור -> חשבון זוויות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 330

• שאלה

  חתכו ריבוע לשלושה חלקים, ואז הרכיבו מהם משולש חד-זווית שכל צלעותיו שונות.

  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים -> חפיפת משולשים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה

• שאלה

  נגיד ששתי פירמידות משיקות זו לזו אם אין להן נקודות פנימיות משותפות והן נחתכות במצולע מישורי לא מנוון. האם ייתכן ש 8 פירמידות במרחב ישיקו כולם אחת לשנייה? 
  א. אנג'אנס 

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית הוכחה ודוגמה -> בניית דוגמה גאומטריה -> גאומטריה במרחב -> פאונים
  מקורות:
  • תחרות הערים, תשמ"א, אביב, גרסה עיקרית, כיתות י"א-י"ב שאלה 1 נקודות 7

• שאלה

  הוכיחו כי לא קיים פאון בעל `7` מקצועות.

  נושאים:

  קומבינטוריקה -> תורת הגרפים הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במרחב -> פאונים

• שאלה

  הוכיחו שלכל פאון יש שתי פאות עם כמות זהה של מקצועות.

  נושאים:

  קומבינטוריקה -> עקרון שובך היונים קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים

• בניית הטטרהדרון

  יש לי טטרהדרון, או פירמידה משולשת, העשויה משישה מקלות המודבקים זה לזה, כפי שמוצג באיור. האם תוכלו לספור נכונה את מספר הדרכים השונות שבהן ניתן היה להדביק את ששת המקלות הללו יחד כדי ליצור את הפירמידה?

  כמה חברים עבדו על זה יחד בערב אחד, כאשר כל אדם מצטייד בשישה גפרורים כדי לעזור למחשבותיו; אבל התברר שאף שתי תוצאות לא היו זהות. אתם רואים, אם נסיר אחד מהמקלות ונסובב אותו לצד השני, זו תהיה פירמידה שונה. אם נחליף בין שניים מהמקלות התוצאה שוב תהיה שונה. אבל זכרו שניתן להעמיד כל פירמידה על כל אחד מארבעת צדדיה מבלי להיות פירמידה שונה. כמה דרכים יש בסך הכל?

  

  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים גאומטריה -> גאומטריה במרחב -> פאונים
  מקורות: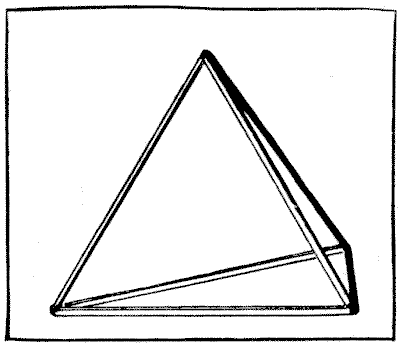
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 280