גאומטריה

גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.

גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים

• מעגל חסום במשולש

  בתוך משולש נמצאת נקודה P, שמרחקיה מהישרים עליהם נמצאות צלעות המשולש הם `d_a,d_b,d_c` נסמן ב R 
  את רדיוס המעגל החוסם את המשולש וב r את רדיוס המעגל החסום במשולש. הראו כי `sqrt(d_a)+sqrt(d_b)+sqrt(d_3)<= sqrt (2R+5r) `.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה -> אי שוויונים
  מקורות:
  • אולימפיאדת גיליס, תש"פ שאלה 7

• אורכי צלעות משולש

  יהי `n > 2` מספר שלם, ויהיו ` t_1,t_2,...,t_n` מספרים ממשיים חיוביים כך ש

  `(t_1+t_2+...+t_n)(1/t_1 + 1/t_2 + ... + 1/t_n) < n^2+1`

  הוכח כי לכל i,j,k כך ש- `1<=i<j<k<=n`, שלשת המספרים `t_i,t_j,t_k` הם אורכי הצלעות של משולש.

  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים אלגברה -> אי שוויונים הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במישור -> אי שוויון המשולש
  מקורות:
  • תחרות גרוסמן, 2006 שאלה 5

• שבילים בפארק משולש

  בפארק יש 3 שבילים ישרים שיוצרים משולש (אין שבילים נוספים). הכניסות לפארק הן באמצעי השבילים, ובכל קודקוד של המשולש תלוי פנס. מכל כניסה מדדו את מרחק ההליכה הקצר ביותר, לאורך שבילי הפארק, עד הפנס בפינה הנגדית. התברר כי 2 מבין 3 המרחקים שווים זה לזה. האם המשולש בהכרח שווה-שוקיים?

  

  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים הוכחה ודוגמה -> בניית דוגמה גאומטריה -> גאומטריה במישור -> אי שוויון המשולש
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 3

• שלושת הכפרים

  יצאתי לדרך אתמול כדי לנסוע במכונית מאייקריפילד לבאטרפורד, אבל בטעות לקחתי את הכביש שעובר דרך צ'יזברי, אשר קרוב יותר לאייקריפילד מאשר לבאטרפורד, והוא שנים עשר מיילים משמאל לכביש הישיר שהייתי צריך לנסוע בו. לאחר שהגעתי לבאטרפורד גיליתי שעברתי שלושים וחמישה מיילים. מהם שלושת המרחקים בין הכפרים הללו, כאשר כל אחד מהם הוא מספר שלם של מיילים? אוסיף ואציין ששלושת הכבישים ישרים לחלוטין.
  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים אלגברה -> בעיות מילוליות גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 69

• המשולש המנותח

   

  חידה טובה היא זו שהג'נטלמן באיור מציג לחבריו. הוא פשוט גזר מנייר משולש שווה צלעות — כלומר, משולש שבו שלוש הצלעות באותו אורך. הוא מציע לחתוך אותו לחמישה חלקים בצורה כזו שהם יתאימו זה לזה וייצרו שניים או שלושה משולשים שווי צלעות קטנים יותר, תוך שימוש בכל החומר בכל מקרה. האם תוכלו לגלות כיצד יש לבצע את החיתוכים?

  זכרו שכאשר הכנתם את חמשת החלקים שלכם, עליכם להיות מסוגלים, כרצוי, לחבר אותם יחד כדי ליצור או את המשולש המקורי הבודד או ליצור שני משולשים או ליצור שלושה משולשים — כולם שווי צלעות.

  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 156

• החידה של פאפוס

  זוהי חידה מאת פאפוס, שחי באלכסנדריה בערך בסוף המאה השלישית. זהו המשפט החמישי בספר השמיני של אוספים מתמטיים שלו. אני מציג אותה בצורה שהצגתי אותה לפני כמה שנים תחת הכותרת "החידה של פאפוס", רק כדי לראות כמה קוראים יגלו שהיא מאת פאפוס עצמו. "לאבא של העלמה הקטנה יש שני פיסות קרטון מלבניות בגדלים שונים, והוא גזר פיסה משולשת מאחת מהן, כך שכאשר היא תלויה בחוט מהנקודה A היא תלויה כשהצד הארוך אופקי לחלוטין, כפי שמוצג באיור. הוא הדהים את הילדה בכך שביקש ממנה למצוא את הנקודה A על הכרטיס השני, כדי להפיק תוצאה דומה כאשר הוא נחתך ותלוי בחוט." כמובן, אסור למצוא את הנקודה על ידי גזירות ניסיון. נקודה מוזרה ויפה מעורבת בהצגת החידה הזו. האם הקורא יכול לגלות אותה?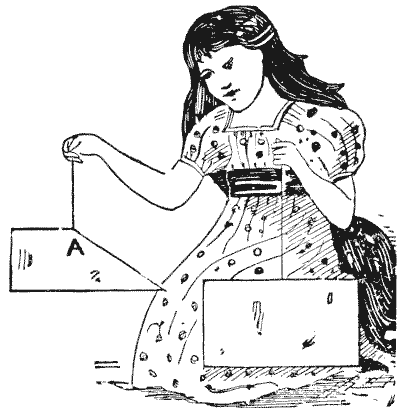
  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 199

• שאלה

  על מעגל מסומנות `2016` נקודות כחולות ונקודה אדומה אחת. נתבונן בכל המצולעים האפשריים בעלי קודקודים בנקודות האלו. איזה מצולעים יש יותר – כאלה שמכילים את הנקודה האדומה או כאלה שכל הקודקודים שלהם כחולים?

  נושאים:

  קומבינטוריקה -> התאמות גאומטריה -> גאומטריה במישור -> מעגלים
  מקורות:
  • אתר האינטרנט problems.ru

• שאלה

  `101` נקודות ממוקמות על מעגל. אילו מצולעים בעלי קודקודים בנקודות האלו יש יותר – מצולעים עם `51` צלעות או מצולעים עם `50` צלעות?

  נושאים:

  קומבינטוריקה -> מקדמים בינומיים ומשולש פסקל קומבינטוריקה -> התאמות גאומטריה -> גאומטריה במישור -> מעגלים

• שאלה

  במרובע אורכי כל האלכסונים וכל הצלעות קטנים מ- 1. הוכח כי ניתן לכסות את המרובע ע"י עיגול ברדיוס 0.9.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במישור -> מעגלים בעיות מינימום ומקסימום
  מקורות:
  • תחרות הערים, תשמ"ב, אביב

• קבוצות במישור

  א. האם קיימת במישור קבוצה A שחיתוכה עם כל מעגל מכיל שתי נקודות בדיוק?

  ב. האם קיימת במישור קבוצה B שחיתוכה עם כל מעגל ברדיוס 1 מכיל שתי נקודות בדיוק?

  נושאים:

  גאומטריה -> גאומטריה במישור -> מעגלים הוכחה ודוגמה -> בניית דוגמה תורת הקבוצות הוכחה ודוגמה -> הוכחה בשלילה בעיות מינימום ומקסימום
  מקורות:
  • תחרות גרוסמן, 2006 שאלה 3