גאומטריה

גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.

גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים

  • חידת החבית

    האנשים באיור מתווכחים על תכולת הנוזל בחבית. אי אפשר לדעת מהו הנוזל הספציפי, מכיוון שאיננו יכולים להסתכל לתוך החבית; לכן נקרא לו מים. איש אחד אומר שהחבית מלאה ביותר מחציה, ואילו השני מתעקש שהיא לא מלאה בחציה. מהי הדרך הקלה ביותר שלהם ליישב את המחלוקת? אין צורך להשתמש במקל, חוט או כלי מדידה מכל סוג שהוא. אני נותן זאת רק כאחת הדוגמאות הפשוטות ביותר לערך של תושייה רגילה בפתרון חידות. בעיות שנראות קשות מאוד ניתנות לעתים קרובות לפתרון בצורה קלה דומה אם רק נשתמש קצת בהיגיון ישר. מקורות:

  • פאזל אריזה

    כפי שכולנו יודעים מניסיון, לעתים קרובות נדרשת תושייה רבה באריזת חפצים לקופסה, אם לא רוצים לבזבז מקום שלא לצורך. אדם סיפר לי פעם שהיו לו מספר רב של כדורי ברזל, שקוטרם בדיוק שני אינץ' כל אחד, והוא רצה לארוז כמה שיותר מהם לתוך קופסה מלבנית באורך `24` `9/10` אינץ', ברוחב `22` `4/5` אינץ' ובעומק `14` אינץ'. מהו המספר הגדול ביותר של כדורים שהוא יכול לארוז בקופסה הזו? מקורות:

  • חידת הסיגר

    הצעתי פעם את החידה הבאה במועדון לונדוני, ולתקופה ניכרת היא ספגה את תשומת הלב של החברים. הם לא הצליחו להבין אותה, וחשבו שהיא בלתי אפשרית לפתרון. ובכל זאת, כפי שאראה, התשובה פשוטה להפליא.

    שני אנשים יושבים ליד שולחן מרובע. אחד מניח סיגר רגיל (שטוח בקצה אחד, מחודד בקצה השני) על השולחן, ואז השני עושה את אותו הדבר, וכן הלאה לסירוגין, בתנאי שאף סיגר לא יגע באחר. איזה שחקן יצליח להניח את הסיגר האחרון, בהנחה שכל אחד מהם ישחק בצורה הטובה ביותר האפשרית? גודל פני השולחן וגודל הסיגר אינם נתונים, אך כדי לשלול את התשובה המגוחכת שהשולחן עשוי להיות כה קטן עד שהוא יכול להכיל רק סיגר אחד, נאמר שהשולחן לא יהיה קטן מ- `2` רגל מרובע והסיגר לא יותר מ- `4`½ אינץ' אורך. עם ההגבלות האלה אתה יכול לקחת כל מימד שתרצה. כמובן שאנו מניחים שכל הסיגרים זהים לחלוטין בכל מובן. האם השחקן הראשון או השחקן השני ינצח?

    מקורות:

  • כשל לוח שחמט

     

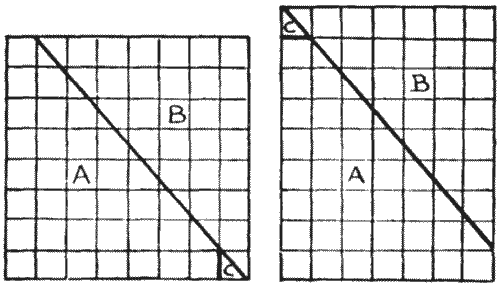
    "הנה דיאגרמה של לוח שחמט," הוא אמר. "אתם רואים שיש שישים וארבעה ריבועים—שמונה על שמונה. עכשיו אני מצייר קו ישר מהפינה השמאלית העליונה, היכן שהריבוע הראשון והשני נפגשים, אל הפינה הימנית התחתונה. אני גוזר לאורך הקו הזה עם המספריים, מחליק למעלה את החלק שסימנתי B, ואז גוזר את הפינה הקטנה C על ידי חיתוך לאורך הקו הישר הראשון. החלק הקטן הזה יתאים בדיוק למקומו למעלה, ועכשיו יש לנו מלבן עם שבעה ריבועים מצד אחד ותשעה ריבועים מצד שני. לכן, יש עכשיו רק שישים ושלושה ריבועים, מכיוון ששבע כפול תשע יוצר שישים ושלוש. לאן לעזאזל נעלם הריבוע האבוד הזה? ניסיתי שוב ושוב לתפוס את הקטן המנוול, אבל הוא תמיד מתחמק ממני. בשביל החיים שלי אני לא מצליח לגלות איפה הוא מסתתר."

    "זה נראה כמו הכשל הישן האחר של לוח השחמט, ואולי ההסבר זהה," אמר רג'ינלד—"שהחלקים לא מתאימים בדיוק."

    "אבל הם כן מתאימים," אמר הדוד ג'ון. "נסה את זה, ותראה."

    מאוחר יותר באותו ערב נראו רג'ינלד וג'ורג' בפינה כשהראשים שלהם ביחד, מנסים לתפוס את הריבוע הקטן החמקמק הזה, וזה רק הוגן לציין שלפני שהם פרשו ללילה הם הצליחו לתפוס את הטרף שלהם, אם כי חלק מחברי החברה לא הצליחו לראות אותו כשנתפס. האם הקורא יכול לפתור את התעלומה הקטנה?

    מקורות:

  • חמש פרוטות

    הנה חידה קשה במיוחד, ולמרות זאת התנאים שלה פשוטים באופן מגוחך. כל קורא יודע איך להניח ארבע פרוטות כך שהן יהיו במרחק שווה זו מזו. כל שעליכם לעשות הוא לסדר שלוש מהן שטוחות על השולחן כך שהן יגעו זו בזו בצורת משולש, ולהניח את הפרוטה הרביעית מעל במרכז. אז, מכיוון שכל פרוטה נוגעת בכל פרוטה אחרת, כולן נמצאות במרחקים שווים זו מזו. עכשיו נסו לעשות את אותו הדבר עם חמש פרוטות - הניחו אותן כך שכל פרוטה תיגע בכל פרוטה אחרת - ותגלו שזה עניין שונה לחלוטין. מקורות:

  • הבלוק המשולב

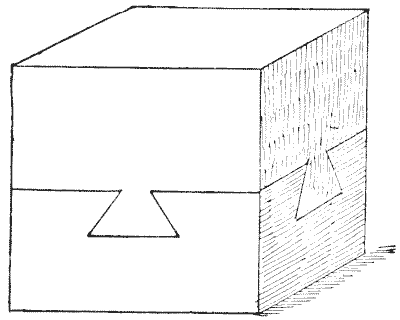    הנה חידה מכנית מוזרה שקיבלתי לפני כמה שנים, אבל אני לא יכול לומר מי המציא אותה לראשונה. היא מורכבת משני גושי עץ מלאים המשולבים זה בזה היטב. בשני הצדדים האנכיים האחרים שאינם נראים, המראה זהה בדיוק לאלה המוצגים. איך חוברו החלקים יחד? כשפרסמתי את החידה הקטנה הזו בעיתון לונדוני קיבלתי (אם כי הם היו לא מוזמנים) די הרבה דגמים, מעץ אלון, מעץ טיק, מהגוני, רוזווד, עץ סאטן, עץ תְרֵשָׁה ועץ אורן; חלקם באורך של חצי רגל, ואחרים בגדלים שונים ממש עד לדגם קטן ועדין בגודל של כחצי אינץ' מרובע. נראה שזה עורר עניין רב. מקורות:

  • הנחת מטבעות חצי פני

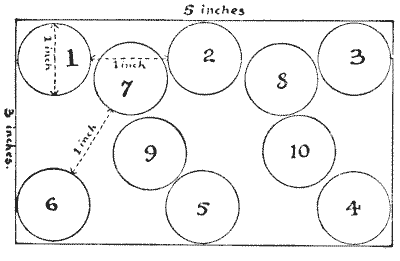    הנה חידה קטנה ומעניינת שהוצעה לי על ידי מר וו. טי. וויט. סמנו על דף נייר שטח מלבני של `5` אינץ' על `3` אינץ', ואז מצאו את המספר הגדול ביותר של מטבעות חצי פני שניתן להניח בתוך המתחם בתנאים הבאים. קוטר של מטבע חצי פני הוא בדיוק אינץ' אחד. הניחו את מטבע חצי הפני הראשון שלכם היכן שתרצו, ואז הניחו את המטבע השני בדיוק במרחק של אינץ' אחד מהראשון, את השלישי במרחק של אינץ' אחד מהשני, וכן הלאה. אסור לאף מטבע חצי פני לגעת במטבע אחר או לחצות את הגבול. האיור שלנו יבהיר את העניין בצורה מושלמת. מטבע מספר `2` נמצא במרחק אינץ' אחד ממספר `1`; מספר `3` במרחק אינץ' אחד ממספר `2`; מספר `4` במרחק אינץ' אחד ממספר `3`; אבל אחרי שמניחים את מספר `10`, איננו יכולים להתקדם בניסיון זה. עם זאת, אפשר היה להכניס עוד כמה מטבעות חצי פני. כמה יכול הקורא להניח? מקורות: