גאומטריה
גאומטריה היא ענף במתמטיקה העוסק בתכונות וביחסים של נקודות, קווים, משטחים, גופים ואנלוגים ממדיים גבוהים יותר. שאלות צפויות כוללות חישוב אורכים, זוויות, שטחים ונפחים של צורות שונות, הבנת משפטים גאומטריים ופתרון בעיות הקשורות לחשיבה מרחבית.
גאומטריה במרחב טריגונומטריה גאומטריה על כדור גאומטריה במישור ווקטורים-
שאלה
חלק את הצורה שבציור לשלושה חלקים שווים בשטחם ובצורתם.
מקורות:
-
שאלה
נתון מצולע משוכלל. על כל צלע בונים משולש ישר זווית ושווה-שוקיים, כך שהצלע היא היתר של המשולש, וקודקוד הראש בפנים המצולע. מחברים את קודקודי הראש של כל המשולשים ומקבלים מצולע (משוכלל, בעל אותו מספר צלעות). כמה צלעות יש למצולע המקורי, אם שטחו של המצולע שהתקבל הוא חצי משטח המצולע המקורי?
מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים -
שאלה
נתון טרפז שווה שוקיים, שאורך השוק שלו a, ואורך האלכסון שלו b, כמו בציור. מצא את הערך הגדול ביותר והקטן ביותר שיכולה לקבל מכפלת הבסיסים (התשובה תלויה ב-`a` וב-`b`).
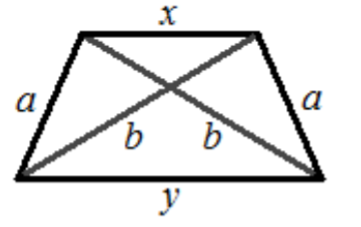 מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה גאומטריה -> גאומטריה במישור -> משפט פיתגורס
מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה גאומטריה -> גאומטריה במישור -> משפט פיתגורס -
שאלה
נתונים שלושה מעגלים שקוטריהם 3, 4, 5. המעגלים הקטנים
משיקים למעגל הגדול מבפנים, בנקודות נגדיות (ראה ציור). המעגלים
הקטנים מחלקים את המעגל הגדול למספר חלקים. ניקח חלק אשר
צורתו "משולש עקום", כלומר, הוא כלוא בין שלוש קשתות של מעגלים שונים. נסמן את
שטחו ב-S, ואת שטח החיתוך של שני העיגולים הקטנים ב-T. חשב את `T/S`מקורות: -
שאלה
נתון מצולע משוכלל. על כל צלע של המצולע בונים משולש שווה-צלעות מחוץ למצולע.
כשמחברים את הקודקודים החדשים של כל המשולשים בזה אחר זה, מקבלים מצולע
משוכלל חדש בעל אותו מספר צלעות כמו המצולע המקורי. כמה צלעות יש למצולע המקורי
אם שטחו של המצולע החדש גדול פי שלושה משטח המצולע המקורי?מקורות:נושאים:גאומטריה -> טריגונומטריה גאומטריה -> חשבון שטחים אלגברה -> משוואות גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים -
שאלה
נתון מגדל בצורת תיבה. גובהו 61 מטרים, ובסיסו הוא ריבוע שצלעו 9 מטרים. על הגג,
בנקודה שנמצאת במרחק של שני מטרים מהקיר הצפוני ושני מטרים מהקיר המערבי, שפכו
מיץ. נמלה נמצאת בתחתית המגדל, בפינה הדרום מזרחית. לנמלה יש חוש ריח מעולה ולכן
היא מרגישה איפה בדיוק נשפך המיץ. מהו המרחק המינימלי שהיא צריכה לעבור בשביל
להגיע לנקודה הזאת? (הנמלה יכול לזחול על הקירות והגג.) מקורות: -
שאלה
על דף לבן ציירו משושה קמור ומחומש קמור. מהו המספר הגדול ביותר של חלקים שאליהם הקווים
מקורות:
בציור יכולים לחלק את הדף? -
שאלה
נתון משולש ABC ומעגל עם רדיוס 10 שחותך כל אחד מהצלעות של המשולש בשתי נקודות: נקודות
P ו-Q על הצלע BC, נקודות K ו-L על הצלע CA, ונקודות M ו-N על הצלע AB, כך שמתקיים `AM = MN = KL = PQ = 2PB = BC/6`. מצאו את שטח המשולש ABC.מקורות:נושאים:גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> מעגלים -
התבוננות לקויה
ההתבוננות שלנו בדברים קטנים היא לעתים קרובות לקויה, והזיכרונות שלנו נוטים מאוד לחלוף. שופט מסוים העיר לאחרונה במקרה שאין לו שום זיכרון מלבישת טבעת הנישואין על אצבעה של אשתו. האם תוכלו לענות נכונה על השאלות הבאות מבלי לראות את המטבעות? באיזה צד של פני מצוין התאריך? יש אנשים כל כך לא מתבוננים שלמרות שהם מטפלים במטבע כמעט כל יום בחייהם, הם מתקשים לענות על השאלה הפשוטה הזו. אם אני מניח פני שטוח על השולחן, כמה פני אחרים אני יכול להניח סביבו, כשכל אחד מהם מונח שטוח על השולחן, כך שכולם יגעו בראשון? הגיאומטריקן כמובן ייתן את התשובה מיד, ולא יצטרך לערוך ניסוי. הוא גם יידע שמאחר שכל המעגלים דומים, אותה תשובה בהכרח תחול על כל מטבע. השאלה הבאה היא מעניינת ביותר לשאול חברה, כאשר כל אדם כותב את תשובתו על פיסת נייר, כך שאף אחד לא ייעזר בתשובות של אחרים. מהו המספר הגדול ביותר של מטבעות של שלושה פני שאפשר להניח שטוחים על פני השטח של חצי כתר, כך שאף מטבע לא יהיה מונח על אחר או יחפוף את פני השטח של חצי הכתר? זה מדהים איזו מגוון תשובות שונות מקבלים לשאלה זו. מעט מאוד אנשים יימצאו את המספר הנכון. כמובן שיש לתת את התשובה מבלי להסתכל על המטבעות. מקורות: -
שעון בתחנת רכבת
שעון תלוי על קיר בתחנת רכבת, שאורכו `71` רגל `9` אינץ' וגובהו `10` רגל `4` אינץ'. אלו הם מידות הקיר, לא של השעון! בזמן שחיכינו לרכבת, שמנו לב שהמחוגים של השעון מצביעים בכיוונים מנוגדים, והיו מקבילים לאחד האלכסונים של הקיר. מה הייתה השעה המדויקת? מקורות:
