קומבינטוריקה
קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.
עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות-
חידת קלף ה-"T"
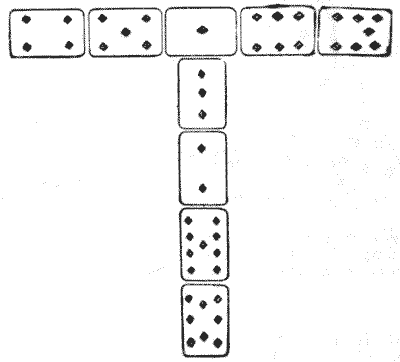 חידה משעשעת עם קלפים היא לקחת את תשעת הקלפים מסדרה אחת, מאס ועד תשע כולל, ולסדר אותם בצורת האות "T," כפי שמוצג באיור, כך שהנקודות בשורה האופקית יספרו אותו דבר כמו אלו בעמודה. בדוגמה הנתונה הם מסתכמים לעשרים ושלוש בשני הכיוונים. עכשיו, זה די קל להשיג סידור נכון יחיד. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת. למרות שהמספר גבוה, הפתרון לא באמת קשה אם נתקוף את החידה בצורה הנכונה. את הדרך ההפוכה המתקבלת על ידי שיקוף האיור במראה לא נספור כשונה, אך כל שאר השינויים במיקומים היחסיים של הקלפים ייספרו כאן. כמה דרכים שונות יש?
מקורות:
חידה משעשעת עם קלפים היא לקחת את תשעת הקלפים מסדרה אחת, מאס ועד תשע כולל, ולסדר אותם בצורת האות "T," כפי שמוצג באיור, כך שהנקודות בשורה האופקית יספרו אותו דבר כמו אלו בעמודה. בדוגמה הנתונה הם מסתכמים לעשרים ושלוש בשני הכיוונים. עכשיו, זה די קל להשיג סידור נכון יחיד. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת. למרות שהמספר גבוה, הפתרון לא באמת קשה אם נתקוף את החידה בצורה הנכונה. את הדרך ההפוכה המתקבלת על ידי שיקוף האיור במראה לא נספור כשונה, אך כל שאר השינויים במיקומים היחסיים של הקלפים ייספרו כאן. כמה דרכים שונות יש?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 383
-
משולשי קלפים
כאן עליך לבחור את תשעת הקלפים, אס עד תשע יהלומים, ולסדר אותם בצורת משולש, בדיוק כפי שמוצג באיור, כך שהנקודות יסתכמו לאותו דבר בכל שלושת הצדדים. בדוגמה הנתונה ניתן לראות שהם מסתכמים ל-`20` בכל צד, אך למספר המסוים אין חשיבות כל עוד הוא זהה בכל שלושת הצדדים. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת.
אם פשוט תסובב את הקלפים כך שאחד משני הצדדים האחרים יהיה הכי קרוב אליך, זה לא ייחשב שונה, כי הסדר יהיה זהה. כמו כן, אם תחליף את המקומות של `4, 9, 5` עם `7, 3, 8`, ובאותו הזמן תחליף את `1` ו-`6`, זה לא יהיה שונה. אבל אם רק תחליף את `1` ו-`6`, זה יהיה שונה, כי הסדר סביב המשולש אינו זהה. הסבר זה ימנע כל ספק לגבי התנאים.
מקורות: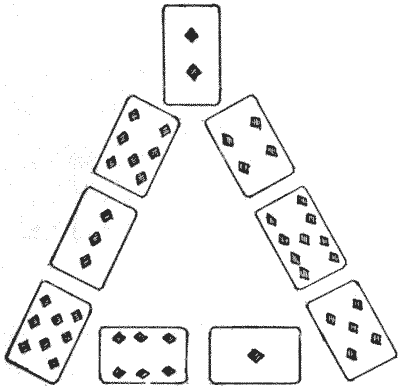
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 384
-
"STRAND" סבלנות
הרעיון לכך עלה לי כששקלתי את משחק הסבלנות שנתתי בתוך Strand Magazine לחודש דצמבר, `1910`, אשר הודפס מחדש בספרו השני של ארנסט ברגהולט Second Book of Patience Games, תחת השם החדש "המלך אלברט".
צרו שתי ערימות קלפים באופן הבא: `9` יהלום, `8` עלה, `7` יהלום, `6` עלה, `5` יהלום, `4` עלה, `3` יהלום, `2` עלה, `1` יהלום, ו-`9` תלתן, `8` תלתן, `7` תלתן, `6` תלתן, `5` תלתן, `4` תלתן, `3` תלתן, `2` תלתן, `1` תלתן, כאשר ה-`9` של יהלומים בתחתית ערימה אחת וה-`9` של תלתן בתחתית הערימה האחרת. המטרה היא להחליף את העלים עם התלתנים, כך שהיהלומים והתלתנים עדיין יהיו בסדר מספרי בערימה אחת והתלתנים והעלים בערימה השנייה. ישנם ארבעה מקומות פנויים בנוסף לשני המקומות שתפוסים על ידי הערימות, וניתן להניח כל קלף על מקום פנוי, אבל ניתן להניח קלף רק על קלף אחר בעל ערך גבוה יותר הבא אחריו — אס על שתיים, שתיים על שלוש וכן הלאה. נדרשת סבלנות כדי לגלות את הדרך הקצרה ביותר לעשות זאת. כאשר ישנם ארבעה מקומות פנויים, ניתן לערום ארבעה קלפים בשבעה מהלכים, עם שלושה מקומות בלבד ניתן לערום אותם בתשעה מהלכים, ועם שני מקומות אי אפשר לערום יותר משני קלפים. כאשר יש לך תפיסה של עובדות אלה ודומות להן, תוכל להסיר מספר קלפים בשלמותם ולרשום `7, 9`, או כל מספר המהלכים הנדרש. הקיצור ההדרגתי של המשחק הוא מרתק, והניסיונות הראשונים הם ארוכים באופן מפתיע.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 385
-
שחקני הכדורגל
"זהו משחק נפלא!" נשמע חובב נלהב קורא. "בסיום העונה שעברה, מבין שחקני הכדורגל שאני מכיר, לארבעה נשברה זרוע שמאל, לחמישה נשברה זרוע ימין, לשניים זרוע ימין הייתה בריאה, ולשלושה זרוע שמאל הייתה בריאה." האם תוכלו לגלות מההצהרה הזו מהו המספר הקטן ביותר של שחקנים שהדובר יכול היה להכיר?
כלל לא נובע מכך שהיו ארבעה עשר אנשים, מכיוון שלדוגמה, שניים מהאנשים ששברו את זרוע שמאל יכולים להיות גם שניים מאלה שהייתה להם זרוע ימין בריאה.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 389
-
משחק החלוקים
הנה משחק חידה קטן ומעניין שנהגתי לשחק עם מכר על החוף בסלוקומב-און-סי. שני שחקנים מניחים מספר אי זוגי של חלוקים, נניח חמישה עשר, ביניהם. לאחר מכן כל אחד בתורו לוקח אחד, שניים או שלושה חלוקים (כפי שהוא בוחר), והמנצח הוא זה שמקבל מספר אי זוגי. לכן, אם אתה מקבל שבע והיריב שלך שמונה, אתה מנצח. אם אתה מקבל שש והוא מקבל תשע, הוא מנצח. האם השחקן הראשון או השני אמור לנצח, וכיצד? לאחר שפתרתם את השאלה עם חמישה עשר חלוקים, נסו שוב עם, למשל, שלושה עשר. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 392
-
שני הצריחים
זוהי משחק חידה לשני שחקנים. לכל שחקן יש צריח אחד. השחקן הראשון מניח את הצריח שלו על כל משבצת בלוח שהוא בוחר, ואז השחקן השני עושה את אותו הדבר. עכשיו הם משחקים בתורות, כאשר המטרה של כל תור היא ללכוד את הצריח של היריב. אבל במשחק הזה אי אפשר לשחק דרך קו תקיפה מבלי להילכד. כלומר, אם בתרשים זה תורו של השחור לשחק, הוא לא יכול להזיז את הצריח שלו למשבצת של הפרש של המלך שלו, או למשבצת של הצריח של המלך שלו, כי הוא ייכנס ל"קו האש" כשהוא עובר על פני המשבצת של הרץ של המלך שלו. מאותה סיבה הוא לא יכול לעבור לצריח של המלכה שלו במשבצת השביעית או השמינית. עכשיו, המשחק לעולם לא יכול להסתיים בתיקו. במוקדם או במאוחר אחד הצריחים חייב ליפול, אלא אם כן, כמובן, שני השחקנים מבצעים את האבסורד של לא לנסות לנצח. הטריק לנצח הוא פשוט להפליא כשאתה יודע אותו. האם אתה יכול לפתור את החידה? מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון קומבינטוריקה -> צביעות -> צביעת שחמט
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון קומבינטוריקה -> צביעות -> צביעת שחמט- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 393
-
חתול בפינה
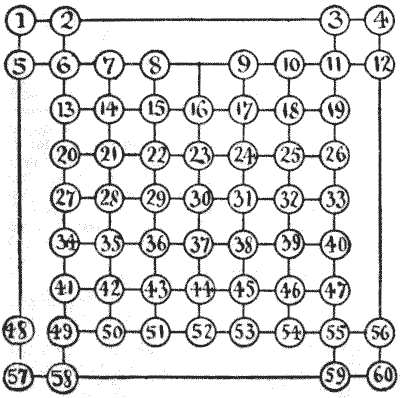
גרסה זו של החידה האחרונה משוחקת גם היא על ידי שני אנשים. אחד מניח כלי משחק על מספר `6`, והשני מניח כלי משחק על מספר `55`, והם משחקים בתורות על ידי הזזת הכלי לכל מספר אחר בקו. אם היריב שלך עובר בכל עת לאחד הקווים שאתה תופס, או אפילו חוצה אחד מהקווים שלך, אתה מיד לוכד אותו ומנצח. ניקח משחק המחשה.
א' זז מ-`55` ל-`52`; ב' זז מ-`6` ל-`13`; א' מתקדם ל-`23`; ב' הולך ל-`15`; א' נסוג ל-`26`; ב' נסוג ל-`13`; א' מתקדם ל-`21`; ב' נסוג ל-`2`; א' מתקדם ל-`7`; ב' הולך ל-`3`; א' זז ל-`6`; ב' חייב כעת ללכת ל-`4`; א' מתבסס ב-`11`, ויש ללכוד את ב' במהלך הבא מכיוון שהוא נאלץ לחצות קו שעליו עומד א'. שחקו זאת שוב ותבינו את המשחק ישירות. כעת, החלק החידתי של המשחק הוא זה: איזה שחקן צריך לנצח, וכמה מהלכים נחוצים?
מקורות:נושאים:קומבינטוריקה -> תורת המשחקים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 394
-
משחק חידה מלחמתי
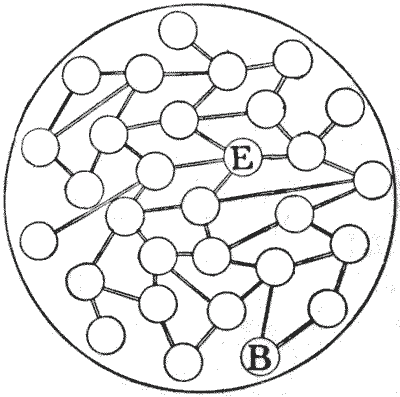 הנה עוד משחק חידה. שחקן אחד, המייצג את הגנרל הבריטי, מניח כלי בנקודה B, והשחקן השני, המייצג את האויב, מניח את הכלי שלו בנקודה E. הבריטי עושה את ההתקדמות הראשונה לאורך אחת הדרכים לעיר הבאה, ואז האויב עובר לאחת הערים הקרובות אליו, וכן הלאה בתורות, עד שהגנרל הבריטי מגיע לאותה עיר כמו האויב ולוכד אותו. למרות שכל אחד חייב תמיד לנוע לאורך דרך לעיר הבאה בלבד, והשחקן השני רשאי לעשות כמיטב יכולתו כדי להימנע מלכידה, הגנרל הבריטי (כפי שאנו אמורים להניח, מהאנלוגיה של החיים האמיתיים) חייב לנצח ללא טעות. אבל איך? זאת השאלה.
מקורות:נושאים:קומבינטוריקה -> תורת המשחקים
הנה עוד משחק חידה. שחקן אחד, המייצג את הגנרל הבריטי, מניח כלי בנקודה B, והשחקן השני, המייצג את האויב, מניח את הכלי שלו בנקודה E. הבריטי עושה את ההתקדמות הראשונה לאורך אחת הדרכים לעיר הבאה, ואז האויב עובר לאחת הערים הקרובות אליו, וכן הלאה בתורות, עד שהגנרל הבריטי מגיע לאותה עיר כמו האויב ולוכד אותו. למרות שכל אחד חייב תמיד לנוע לאורך דרך לעיר הבאה בלבד, והשחקן השני רשאי לעשות כמיטב יכולתו כדי להימנע מלכידה, הגנרל הבריטי (כפי שאנו אמורים להניח, מהאנלוגיה של החיים האמיתיים) חייב לנצח ללא טעות. אבל איך? זאת השאלה.
מקורות:נושאים:קומבינטוריקה -> תורת המשחקים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 395
-
תעלומת גפרורים
הנה משחק קטן שתנאיו פשוטים באופן ילדותי. אבל הוא ראוי לחקירה.
מר סטאבס משך שולחן קטן בינו לבין חברו, מר וילסון, ולקח קופסת גפרורים, שממנה ספר שלושים.
"הנה שלושים גפרורים," אמר. "אני מחלק אותם לשלוש ערימות לא שוות. תן לי לראות. יש לנו `14, 11` ו-`5`, במקרה. עכשיו, שני השחקנים מושכים לסירוגין כל מספר מכל ערימה אחת, ומי שמושך את הגפרור האחרון מפסיד במשחק. זה הכל! אני אשחק איתך, וילסון. הרכבתי את הערימות, אז יש לך את התור הראשון."
"מכיוון שאני יכול למשוך כל מספר," אמר מר וילסון, "נניח שאני מציג את המתינות הרגילה שלי ואקח את כל ערימת ה-`14`."
"זה הכי גרוע שיכולת לעשות, כי זה מפסיד מיד. אני לוקח `6` מה-`11`, ומשאיר שתי ערימות שוות של `5`, ולהשאיר שתי ערימות שוות זה ניצחון בטוח (פרט לחריג היחיד של `1, 1`), כי מה שלא תעשה בערימה אחת אני יכול לחזור עליו בשנייה. אם אתה משאיר `4` בערימה אחת, אני משאיר `4` בשנייה. אם אתה משאיר רק `1` בערימה אחת, אז אני לוקח את כל הערימה השנייה. אם אתה לוקח את כל הערימה האחת, אני לוקח את הכל מלבד אחד בשנייה. לא, אסור לך אף פעם להשאיר שתי ערימות, אלא אם כן הן ערימות שוות ויותר מ-`1, 1`. בוא נתחיל שוב."
"בסדר גמור," אמר מר וילסון. "אני אקח `6` מה-`14`, ואשאיר לך `8, 11, 5`."
מר סטאבס אז השאיר `8, 11, 3`; מר וילסון, `8, 5, 3`; מר סטאבס, `6, 5, 3`; מר וילסון, `4, 5, 3`; מר סטאבס, `4, 5, 1`; מר וילסון, `4, 3, 1`; מר סטאבס, `2, 3, 1`; מר וילסון, `2, 1, 1`; שאותו מר סטאבס צמצם ל-`1, 1, 1`.
"עכשיו ברור לחלוטין שאני חייב לנצח," אמר מר סטאבס, כי אתה חייב לקחת `1`, ואז אני לוקח `1`, ומשאיר לך את הגפרור האחרון. אף פעם לא היה לך סיכוי. יש בדיוק שלושה עשר דרכים שונות שבהן ניתן לקבץ את הגפרורים בהתחלה לניצחון בטוח. למעשה, הקבוצות שנבחרו, `14, 11, 5`, הן ניצחון בטוח, כי על מה שהיריב שלך ישחק יש קבוצה מנצחת אחרת שאתה יכול להבטיח, וכך הלאה עד הגפרור האחרון."
מקורות:נושאים:קומבינטוריקה -> תורת המשחקים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 396
-
משחק הקוביות המונטנגרי
מסופר כי לתושבי מונטנגרו יש משחק קוביות קטן שהוא גם גאוני וגם ראוי לחקירה. שני השחקנים בוחרים תחילה שני זוגות שונים של מספרים אי-זוגיים (תמיד גבוהים מ-`3`), ואז מטילים לסירוגין שלוש קוביות. מי שמטיל ראשון את הקוביות כך שסכומן הוא אחד מהמספרים שבחר מנצח. אם שניהם מצליחים בשתי הטלות עוקבות, זה תיקו והם מנסים שוב. לדוגמה, שחקן אחד יכול לבחור `7` ו-`15` והשני `5` ו-`13`. לאחר מכן, אם השחקן הראשון מטיל כך ששלוש הקוביות מסתכמות ל-`7` או `15`, הוא מנצח, אלא אם כן השחקן השני מקבל `5` או `13` בהטלה שלו.
החידה היא לגלות אילו שני זוגות מספרים יש לבחור כדי לתת לשני השחקנים סיכוי שווה בדיוק.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 397